алгебра логики лекции и практика

18.04.202319.04.2023 admin 0 Comments

Лекция «основы алгебры логики»

Ищем педагогов в команду «Инфоурок»

Основные понятия алгебры логики. Логические основы эвм.

Высказывания могут быть простыми и сложными. Простые соответствуют алгебраическим переменным, а сложные являются аналогом алгебраических функций. Функции могут получаться путем объединения переменных с помощью логических действий.

Самой простой логической операцией является операция НЕ(по-другому ее часто называют отрицанием, дополнением или инверсией и обозначают NOTX или. Результат отрицания всегда противоположен значению аргумента.

Логическая операция НЕ является унарной, т.е. имеет всего один операнд. В отличие от нее, операции И (AND) и ИЛИ (OR) являются бинарными, так как представляют собой результаты действий над двумя логическими величинами.

Операцию НЕ можно задать в виде таблицы

Логическое И еще часто называют конъюнкцией, или логическим умножением.

Операция И имеет результат «истина» только в том случае, если оба ее операнда истинны. Принято обозначать значком «&»либо «^»

Например, рассмотрим высказывание «Для остановки ОС «Windows’95» требуется процессор не ниже 80386 и не менее 4 Мбайт оперативной памяти». Из него следует, что установка будет успешной только при одновременном выполнении обоих условий: даже если у вас в машине Pentium, но мало ОЗУ (равно как и при 8 Мбайт ОЗУ процессор 80286), «Windows’95» работать откажется.

X Y

Приведенные выше таблицы значений переменных для логических операций называются таблицами истинности. В них указываются все возможные комбинации логических переменных Х и Y, а также соответствующие им результаты операций. Таблица истинности может рассматриваться в качестве одного из способов задания логической функции.

Операции И, ИЛИ, НЕ образуют полную систему логических операций, из которой можно построить сколь угодно сложное логическое выражение.

В вычислительной технике также часто используется операция исключающее ИЛИ (XOR), которая отличается от обыкновенного ИЛИ только при Х=1 иY=l.

Как видно из табл. 1.2, операция XOR фактически сравнивает на совпадение два двоичных разряда. Хотя теоретически основными базовыми логическими операциями всегда называют именно И, ИЛИ, НЕ, на практике по технологическим причинам в качестве основного логического элемента используется элемент И-НЕ(последняя колонка в табл. 1.2).

Таблица 1.2. Дополнительные логические операции

Источник

Основы алгебры логики

Тематический план

Общее

Тема 5

Тема 6

Тема 7

Тема 8

Тема 9

Тема 10

Информатика не может существовать без такого важного раздела математики, который называется алгеброй логики. В данной статье будет рассказана основополагающая информация по данной теме, обозначены её главные правила и законы.

Что такое алгебра и алгебра логики

Алгебра — это раздел математики, который обобщенно можно охарактеризовать, как расширение и обобщение арифметики.

Алгебра логики — это раздел математической логики, который исследует операции над высказываниями.

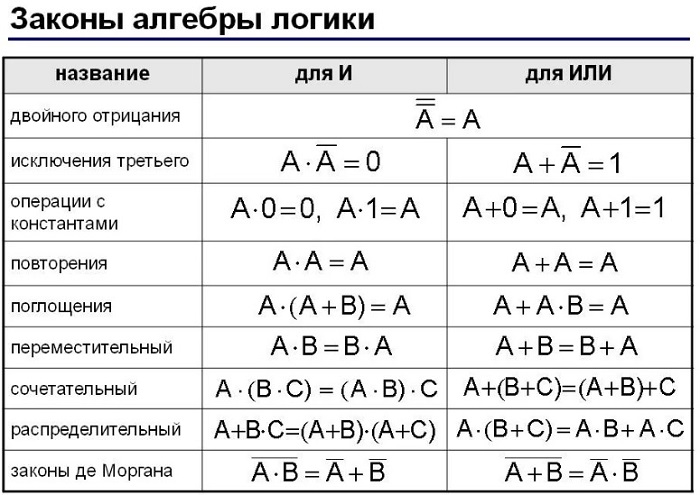
Законы алгебры логики

Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.

Основные законы алгебры логики представлены в таблице:

Логические выражения

В информатике предоставляется два вида высказываний: простое и сложное.

Простое — это утверждение, которое обычно обозначается в виде предложения и про него можно сказать — ложное оно или истинное.

Нью-Йорк — столица США (ложное);

в России 1117 городов (верное).

Сложное высказывание обозначает некий набор простых утверждений, которые связаны логическими процессами.

Идёт дождь, а у меня нет зонта.

Основные логические операции

Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.

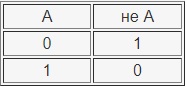
Логическое отрицание (инверсия) —НЕ

Таблица истинности инверсии:

Результаты операции НЕ следующие:

если исходное выражение истинно, то результат его отрицания будет ложным;

если исходное выражение ложно, то результат его отрицания будет истинным.

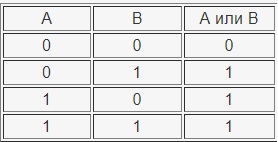
Логическое сложение (дизъюнкция, объединение) — ИЛИ

Понятие «Логическое ИЛИ» также можно заменить понятием «Дизъюнкция». Данная операция обозначается знаками — ИЛИ, OR, ||, |.

Но есть небольшое отличие: в «Логическом И» результат отрицания равен единице, если оба обозначения равны единице, а в «Логическом ИЛИ» итог равен единице, если одно из обозначений равно единице.

Таблица истинности операции ИЛИ:

Логическое умножение(конъюнкция) — И

В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.

За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).

При всех остальных значениях операция будет ложной.

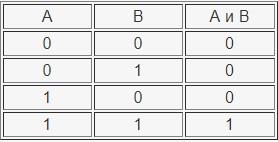
Таблица истинности операции И приведена ниже:

Логическое следование (импликация) — ЕСЛИ ТО

Данная программа имеет также название «Импликация». Она образуется из двух высказываний, которые соединяет: «если. то».

Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if. then.

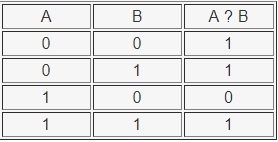
Таблица истинности операции ЕСЛИ ТО выглядит так:

Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.

И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.

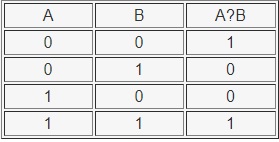
Таблица истинности операции эквивалентности:

Источник

Основные понятия алгебры логики. Функции алгебры логики. Основные логические эквивалентности

Предисловие

Учебное пособие предназначено для студентов-бакалавров, по направлениям «Информатика и вычислительная техника», «Программная инженерия», «Информационная безопасность», студентов, обучающихся по специальности «Применение и эксплуатация автоматизированных систем специального назначения» и схожим направлениям и специальностям на начальном периоде обучения.

Для изучения данного учебного пособия, с одной стороны, не требуется каких-либо специальных знаний, но, с другой стороны, пособие призвано показать, как традиционные понятия и алгоритмы, преломляются при проектировании реальных вычислительных устройств в зависимости от тех целей, которые перед этим устройством ставятся: минимизация оборудования или используемой элементной базы, минимизация времени выполнения какой-либо команды или упрощения используемого устройства управления, АЛУ и других критериев.

В пособии приводятся основные понятия алгебры логики. Особое внимание уделяется тем элементарным логическим функциям, которые находят наибольшее распространение в ЭВМ: конъюнкция, дизъюнкция, штрих Шеффера, стрелка Пирса, сумма по модулю два и их основным эквивалентностям.

Рассматриваются различные подходы к одному из важнейших для вычислительной техники вопросов математической логики – минимизации логических функций. Рассмотрены вопросы минимизации функций алгебры логики на основе теоремы Квайна, минимизирующих карт (диаграмм Вейча), метода Квайна – МакКласки, а также минимизации не полностью определённых логических функций.

Дано схемотехническое представление элементов, выполняющих основные операции функций алгебры логики, а также некоторых других основных элементов ЭВМ, знание функционирования которых позволит лучше понять выполнение арифметических операций в компьютере, а также функционирование компьютера в целом.

Рассмотрены формы представления чисел в прямом, обратном и дополнительном кодах и методики выполнения основных арифметических операций в различных кодах, а также особые случаи, возникающие при выполнении этих операций. Показано, как влияет использование того или иного алгоритма выполнения арифметической операции на структуру ЭВМ и ее производительность.

Весь материал проиллюстрирован большим количеством примеров, которые позволят на практике закрепить изложенные в пособии теоретические положения.

Знание изложенного материала поможет в дальнейшем легче осваивать дисциплины, связанные с аппаратной реализацией современных средств вычислительной техники: схемотехнику, построение запоминающих устройств, интерфейсы, архитектуру микропроцессоров и другие курсы.

Источник

Алгебра логики

Содержание:

Алгебра логики является частью, разделом бурно развивающейся сегодня науки — дискретной математики. Дискретная математика занимается изучением свойств структур конечного характера, которые возникают как внутри математики, так и в ее приложениях.

К числу структур, изучаемых дискретной математикой, могут быть отнесены конечные группы, конечные графы, математические модели преобразователей информации типа конечных автоматов или машин Тьюринга и др. Математический аппарат алгебры логики широко используется в информатике, в частности, в таких ее разделах, как проектирование ЭВМ, теория автоматов, теория алгоритмов, теория информации, целочисленное программирование и т. д. Алгебра логики.

Понятие высказывания Алгебра логики изучает свойства функций, у которых и аргументы, и значения принадлежат заданному двухэлементному множеству (например,). Иногда вместо термина «алгебра логики» употребляют термин «двузначная логика». Отцом алгебры логики по праву считается английский математик XIX столетия Джордж Буль.

Именно он построил один из разделов формальной логики в виде некоторой «алгебры», аналогичной алгебре чисел, но не сводящейся к ней. Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться не только над числами, но и над другими математическими объектами.

Существуют алгебры натуральных чисел, многочленов, векторов, матриц, множеств и т. д. Дж. Буль (1815-1864) Долгое время алгебра логики была известна достаточно узкому классу специалистов.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Прошло почти 100 лет со времени создания алгебры логики Дж. Булем, прежде чем в 1938 году выдающийся американский математик и инженер Клод Шеннон (1916-2001) показал, что алгебра логики применима для описания самых разнообразных процессов, в том числе функционирования ре-лейно-контактных и электронно-ламповых схем. Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики).

Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна » устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным. Что же является высказыванием в формальной логике?

Определение 1. Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).

Возможно вам будут полезны данные страницы:

Это словесное определение, не являющееся математически точным, только на первый взгляд кажется удовлетворительным. Оно отсылает проблему определения высказывания к проблеме определения истинности или ложности данного языкового образования. Если рассматривать в качестве высказываний любые утвердительные предложения, то это быстро приводит к парадоксам и противоречиям. Например, предложению «Это предложение является ложным» невозможно приписать никакого значения истинности без того, чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит его смыслу. Если же принять, что предложение ложно, то отсюда следует, что предложение на самом деле истинно.

Определение 2. Высказывание называется простым (элементарным)I, если никакая его часть не является высказыванием.

Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Из двух числовых выражений можно составить высказывание, соединив их знаком равенства или неравенства. Сами числовые выражения высказываниями не являются. Не являются высказываниями и равенства или неравенства, содержащие переменные. Например, предложение «» становится высказыванием при замене переменной каким-либо конкретным значением. Предложения типа «» называют предикатами. Алгебра логики отвлекается от смысловой содержательности высказываний.

Мы можем договориться, что абсурдное по смыслу высказывание «Крокодилы летают» является истинным, и с этим значением высказывания будем работать. Вопрос о том, летают крокодилы или нет, может волновать зоологов, но никак не математиков: им этот потрясающий факт безразличен. Введение таких ограничений дает возможность изучать высказывания алгебраическими методами, позволяет ввести операции над элементарными высказываниями и с их помощью строить и изучать составные высказывания. В информатике для точного определения понятия высказывания строятся ограниченные системы форм высказываний (формальный язык), которые используются при описании алгоритмических языков, в информационных системах, для строгого формального описания алгоритмов и т. д.

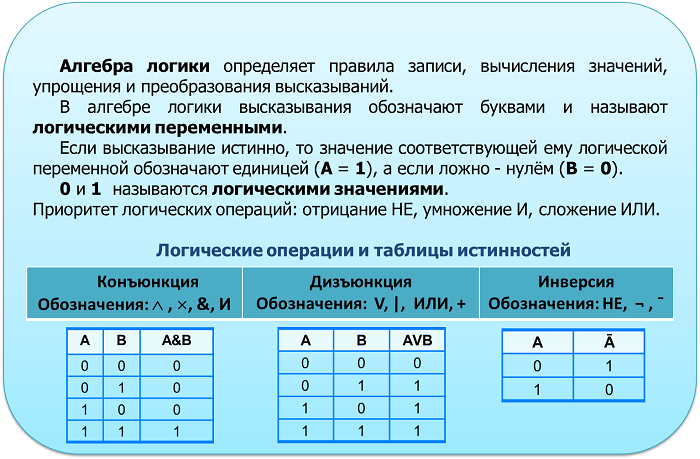
Логические операции. Таблицы истинности

Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает сложное высказывание при всех возможных значениях простых высказываний. В алгебре логики логические связки и соответствующие им логические операции имеют специальные названия и обозначаются следующим образом:

Введем перечисленные логические операции формальным образом. Высказывание, составленное из двух высказываний путем объединения их связкой «и», называется конъюнкцией или логическим умножением. Высказывая конъюнкцию, мы утверждаем, что выполняются оба события, о которых идет речь в составляющих высказываниях.

Например, сообщая: <Ивановы привезли на зиму уголь и закупили дрова на растопку камина>, мы выражаем в одном высказывании свое убеждение в том, что произошли оба этих события.

Определение 3. Конъюнкция — логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Логическая операция конъюнкция определяется следующей таблицей, которую называют таблицей истинности:

Рассмотрим два высказывания = <Завтра будет мороз) и <Завтра будет идти снег>. Очевидно, новое высказывание = <Завтра будет мороз, и завтра будет идти снег>истинно только в том случае, когда одновременно истинны высказывания а именно, когда истинно, что завтра будет и мороз, и снег.

Высказывание будет ложно во всех остальных случаях: будет идти снег, но будет оттепель (т. е. не будет мороза); мороз будет, а снег не будет идти; не будет мороза, и снег не будет идти. В русском языке конъюнкции соответствует не только союз «и», но и другие речевые обороты, например связки «а» или «но».

Высказывание, состоящее из двух высказываний, объединенных связкой «или», называется дизъюнкцией или логическим сложением, нестрогой дизъюнкцией.

В высказываниях, содержащих связку «или», указывается на существование двух возможных событий, из которых хотя бы одно должно быть осуществлено. Например, сообщая: <Петя читает книгу или пьет чай), мы имеем в виду, что хотя бы что-либо одно Петя делает. При этом Петя может одновременно читать книгу и пить чай. И в этом случае дизъюнкция будет истинна.

Определение 4. Дизъюнкция — логическая операция, которая каждым двум элементарным высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.

Логическая операция дизъюнкция определяется следующей таблицей истинности:

Дизъюнкция истинна, когда хотя бы одно из двух образующих ее высказываний истинно. Рассмотрим два высказывания = <Колумб был в Индии) и = <Колумб был в Египте>. Очевидно, новое высказывание = <Колумб был в Индии или Колумб был в Египте>истинно как в случае, если Колумб был в Индии, но не был в Египте, так и в случае, если он не был в Индии, но был в Египте, а также в случае, если он был и в Индии, и в Египте. Но это высказывание будет ложно, если Колумб не был ни в Индии, ни в Египте.

В отличие от обычной дизъюнкции (связка «или»), в высказывании, являющемся разделительной дизъюнкцией, мы утверждаем, что произойдет только одно событие из двух. Например, сообщая: <Петя сидит на трибуне А либо на трибуне Б>, мы утверждаем, что Петя сидит либо только на трибуне А, либо только на трибуне Б.

Определение 5. Строгая, или разделительная дизъюнкция — логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда ровно одно из двух высказываний является истинным.

Логическая операция разделительная дизъюнкция определяется следующей таблицей истинности:

Рассмотрим два высказывания — <Кошка охотится за мышами) и — <Кошка спит на диване). Очевидно, что новое высказывание истинно только в двух случаях: когда кошка охотится за мышами или когда кошка мирно спит. Это высказывание будет ложно, если кошка не делает ни того, ни другого, т. е. когда оба события не происходят. Но это высказывание будет ложным и тогда, когда предполагается, что оба события будут происходить одновременно.

Определение 6. Импликация — логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся ложным тогда и только тогда, когда условие (посылка) — истинно, а следствие (заключение) — ложно.

Логическая операция импликация задается следующей таблицей истинности:

Мы видим, что импликация заведомо истинна, если условие ложно. Другими словами, из неверного условия может следовать все, что угодно. Например, высказывание <Если то крокодилы летают) является истинным. Подавляющее число зависимостей между событиями можно описать с помощью импликации.

Примеры с решением

Пример 1.

Следующие две импликации являются ложными, так как в них посылки истинны, а заключения ложны:

Может показаться странным, что высказывание «Если А, то В>> всегда истинно, если посылка (высказывание Л) ложна. Но для математика это вполне естественно. В самом деле, исходя из ложной посылки, можно путем верных рассуждений получить как истинное, так и ложное утверждение. Допустим, что 1 = 2, тогда и 2 = 1. Складывая эти равенства, получим 3 = 3, т. е. из ложной посылки путем тождественных преобразований мы получили истинное высказывание.

Большинство математических теорем являются импликациями. Однако те импликации, в которых посылки (условия) и заключения (следствия) являются предложениями без взаимной (по существу) связи, не могут играть в науке важной роли. Они являются бесплодными предложениями, так как не ведут к выводам более глубокого содержания.

Логические формулы. Законы алгебры логики

Математики под словом «алгебра» подразумевают науку, которая изучает некие объекты и операции над ними. Например, школьная алгебра (алгебра действительных чисел) изучает действительные числа и операции над ними. Предметом же нашего изучения являются высказывания, операции над ними, а также логические функции. В предыдущих параграфах для обозначения высказываний мы использовали буквы. Как и в алгебре действительных чисел, введем следующие определения.

Определение 9. Логической переменной называется переменная, значением которой может быть любое высказывание.

Логические переменные (далее «переменные») обозначаются латинскими буквами, иногда снабженными индексами, как обычные алгебраические переменные: и т. п.

Понятие логической формулы является формализацией понятия сложного высказывания. Введем его индуктивно. Определение 10. Логической формулой является: 1) любая логическая переменная, а также каждая из двух логических констант — 0 (ложь) и 1 (истина); 2) если А и В — формулы, то В и А*В — тоже формулы, где знак «*» означает любую из логических бинарных операций. Формулой является, например, следующее выражение: Каждой формуле при заданных значениях входящих в нее переменных приписывается одно из двух значений — 0 или 1.

Определение 11. Формулы А и В, зависящие от одного и того же набора переменных называют равносильными или эквивалентными, если на любом наборе значений переменных они имеют одинаковые значения.

Для обозначения равносильности формул используется знак равенства, например А В. В дальнейшем будет показано, что любую формулу можно преобразовать к равносильной ей, в которой используются только аксиоматически введенные операции и отрицание. Для преобразования формул в равносильные важную роль играют следующие равенства, отражающие свойства логических операций, которые по аналогии с алгеброй вещественных чисел будем называть законами:

1) законы коммутативности

2) законы ассоциативности

3) законы поглощения (нуля и единицы)

4) законы дистрибутивности

5) закон противоречия

6) закон исключенного третьего

7) законы идемпотентности

8) закон двойного отрицания

9) законы де Моргана

10) законы поглощения

Любой из этих законов может быть легко доказан с помощью таблиц истинности.

Пример 2.

Докажем первый закон де Моргана с использованием таблиц истинности. Построим таблицу истинности для левой и правой частей закона.

Так как результирующие столбцы совпали, то формулы, стоящие в левой и правой частях закона, равносильны. Любой из законов алгебры логики может быть доказан путем логических рассуждений.

Пример 3.

Докажем первый закон поглощения путем логических рассуждений. Для этого достаточно показать, что если правая часть истинна, то и левая часть истинна, и что если левая часть истинна, то и правая часть истинна.

Пусть истинна правая часть, т. е. тогда в левой части дизъюнкция истинна по определению дизъюнкции.

Пусть истинна левая часть. Тогда по определению дизъюнкции истинна или формула или формула или обе эти формулы одновременно.

Если ложна, тогда ложна, следовательно, х может быть только истинной. Еще одним способом вывода законов являются тождественные преобразования. Пример 9. Первый закон поглощения можно вывести при помощи законов поглощения единицы и дистрибутивности:

Методы решения логических задач Исходными данными в логических задачах являются высказывания. Эти высказывания и взаимосвязи между ними бывают так сложны, что разобраться в них без использования специальных методов достаточно трудно.

Многие логические задачи связаны с рассмотрением нескольких конечных множеств и связей между их элементами. Для решения таких задач зачастую прибегают к помощи таблиц или графов, при этом успешность решения во многом зависит от удачно выбранной структуры таблицы или графа. Аппарат же алгебры логики позволяет построить формальный универсальный способ решения логических задач.

Рассмотрим, как можно использовать данный способ для решения задач.

Пример 4.

Задача «Уроки логики». На вопрос, кто из трех учащихся изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из учащихся изучал логику?

Решение. Обозначим через высказывания, состоящие в том, что соответственно первый, второй, третий учащийся изучали логику. Из условия задачи следует истинность высказывания Воспользуемся соотношением и упростим исходное высказывание:

Высказывание ложно, а следовательно, ложно и высказывание . Поэтому должно быть истинным высказывание а.это означает, что логику изучал третий учащийся, а первый и второй не изучали. Для решения следующей задачи составим логическое выражение, удовлетворяющее всем условиям, затем заполним для него таблицу истинности. Анализ полученной таблицы истинности позволит получить требуемый результат.

Пример 5.

Задача «Кто виноват?» По обвинению в ограблении перед судом предстали Иванов, Петров, Сидоров. Следствием установлено: 1) если Иванов не виновен или Петров виновен, то Сидоров виновен; 2) если Иванов не виновен, то Сидоров не виновен. Виновен ли Иванов? Решение. Рассмотрим простые высказывания: А = <Иванов виновен>, В = <Петров виновен>, С = <Сидоров виновен>. Запишем на языке алгебры логики факты, установленные следствием: Обозначим — единое логическое выражение для всех требований задачи. Оно истинно. Составим для него таблицу истинности:

Решить данную задачу — значит указать, при каких значениях А полученное сложное высказывание F истинно. Для этого необходимо проанализировать все строки таблицы истинности, где И если хотя бы в одном из таких случаев (Иванов не виновен), то у следствия недостаточно фактов для того, чтобы обвинить Иванова в преступлении. Анализ таблицы показывает, что высказывание истинно только в тех случаях, когда истинно, т. е. Иванов в ограблении виновен. Иногда, для того чтобы решить задачу, нет необходимости составлять единое логическое выражение, удовлетворяющее всем условиям задачи, достаточно построить таблицу истинности, отражающую каждое условие задачи, и проанализировать ее.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Беременность и дети

алгебра логики лекции и практика

Лекция «основы алгебры логики»

Основы алгебры логики