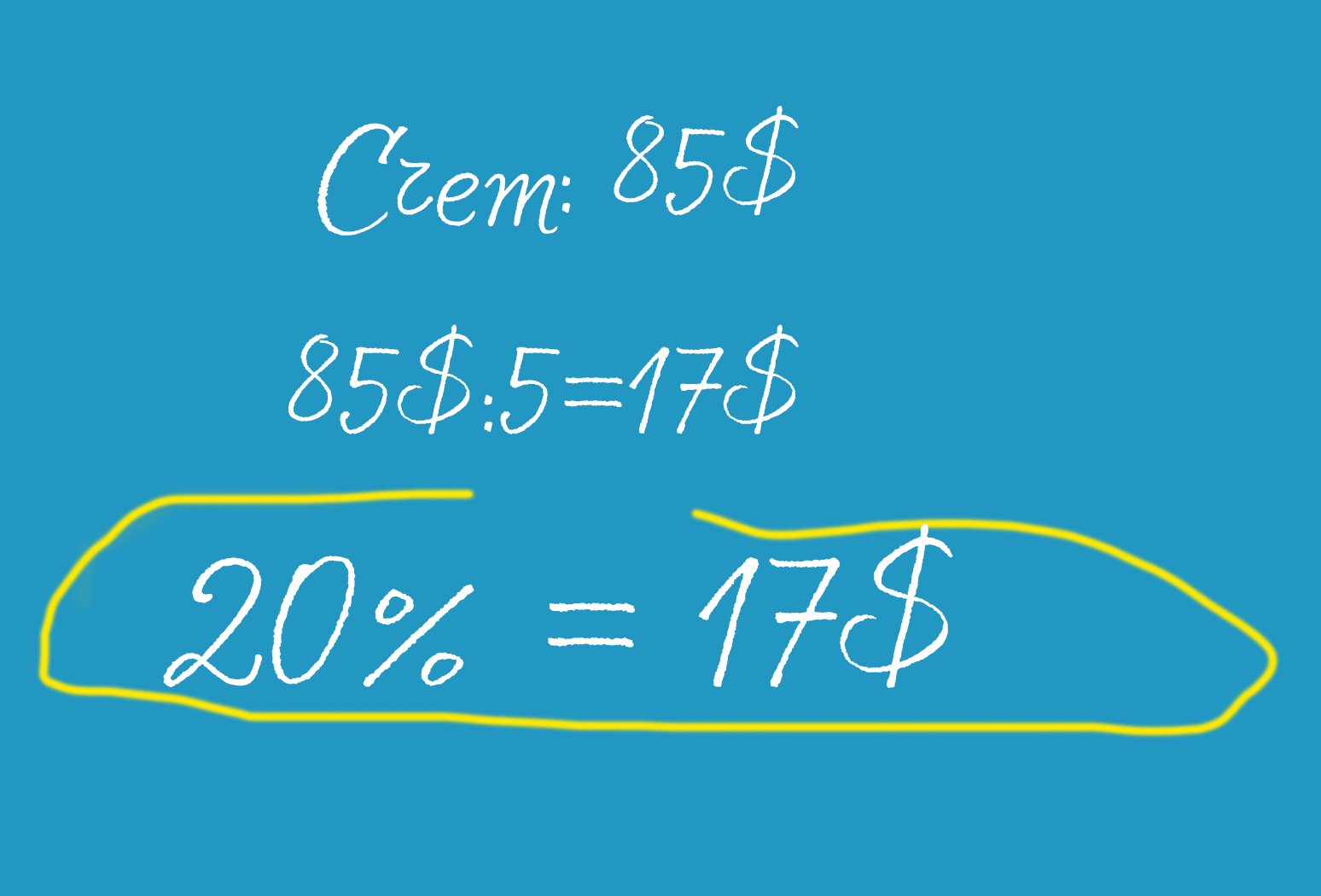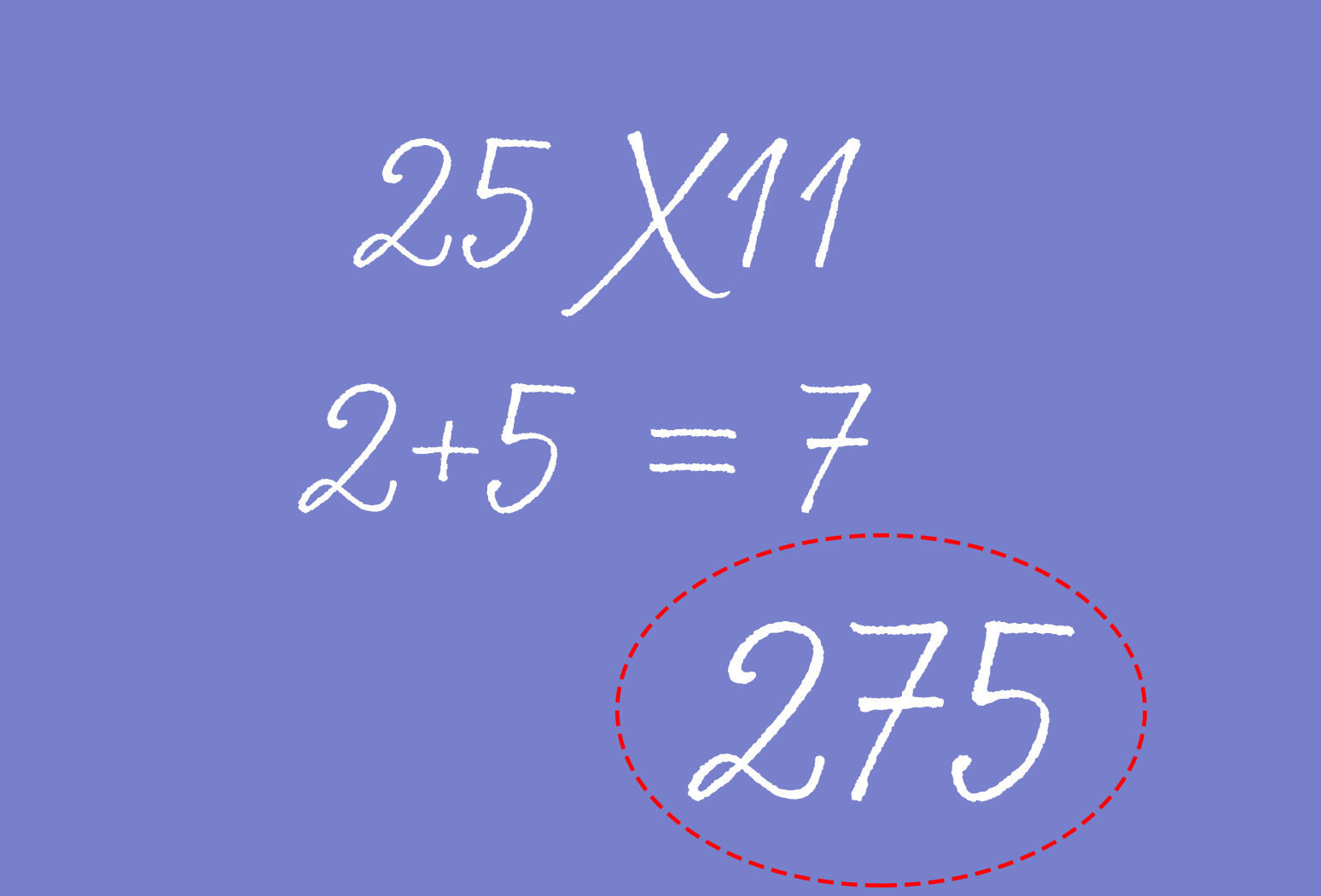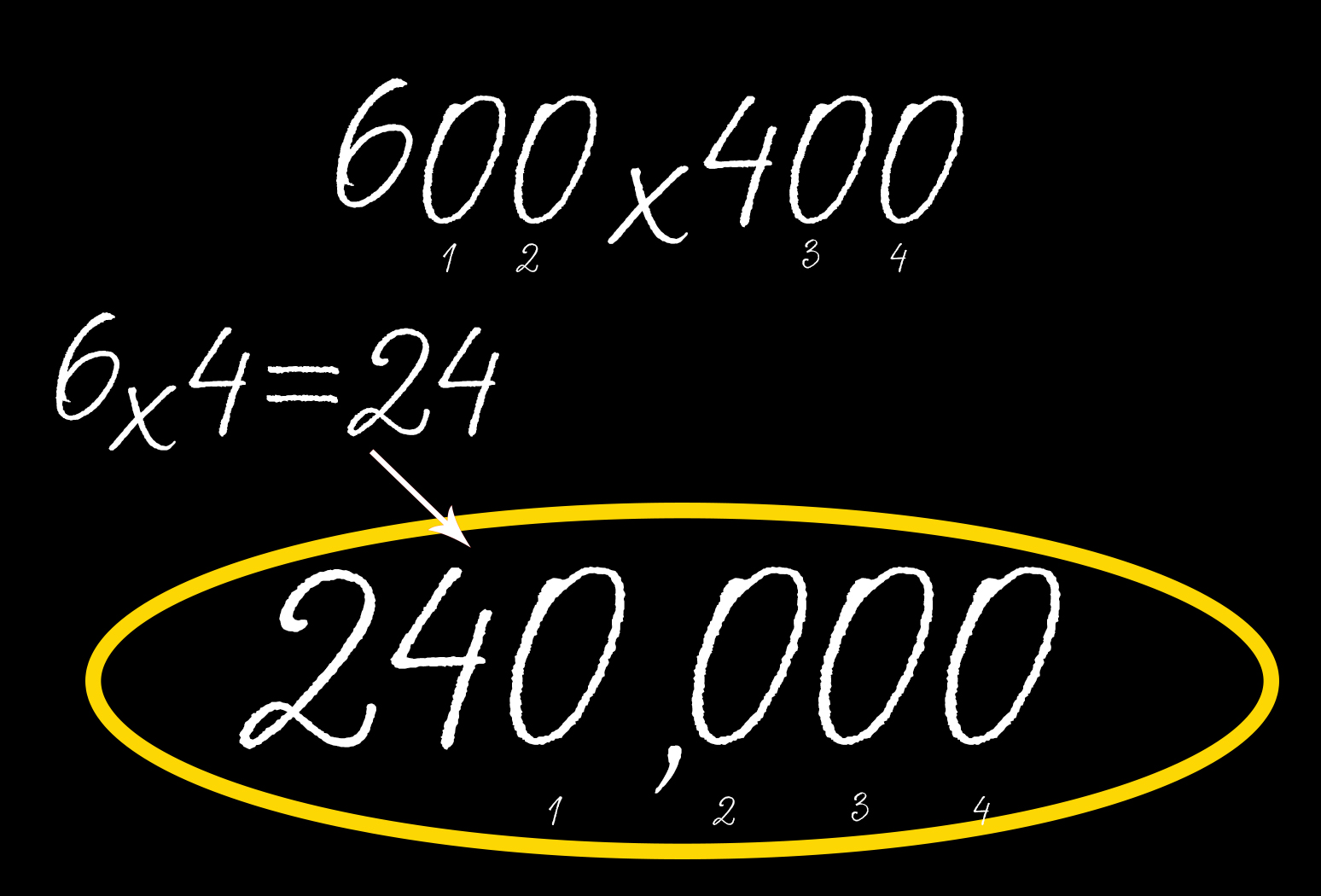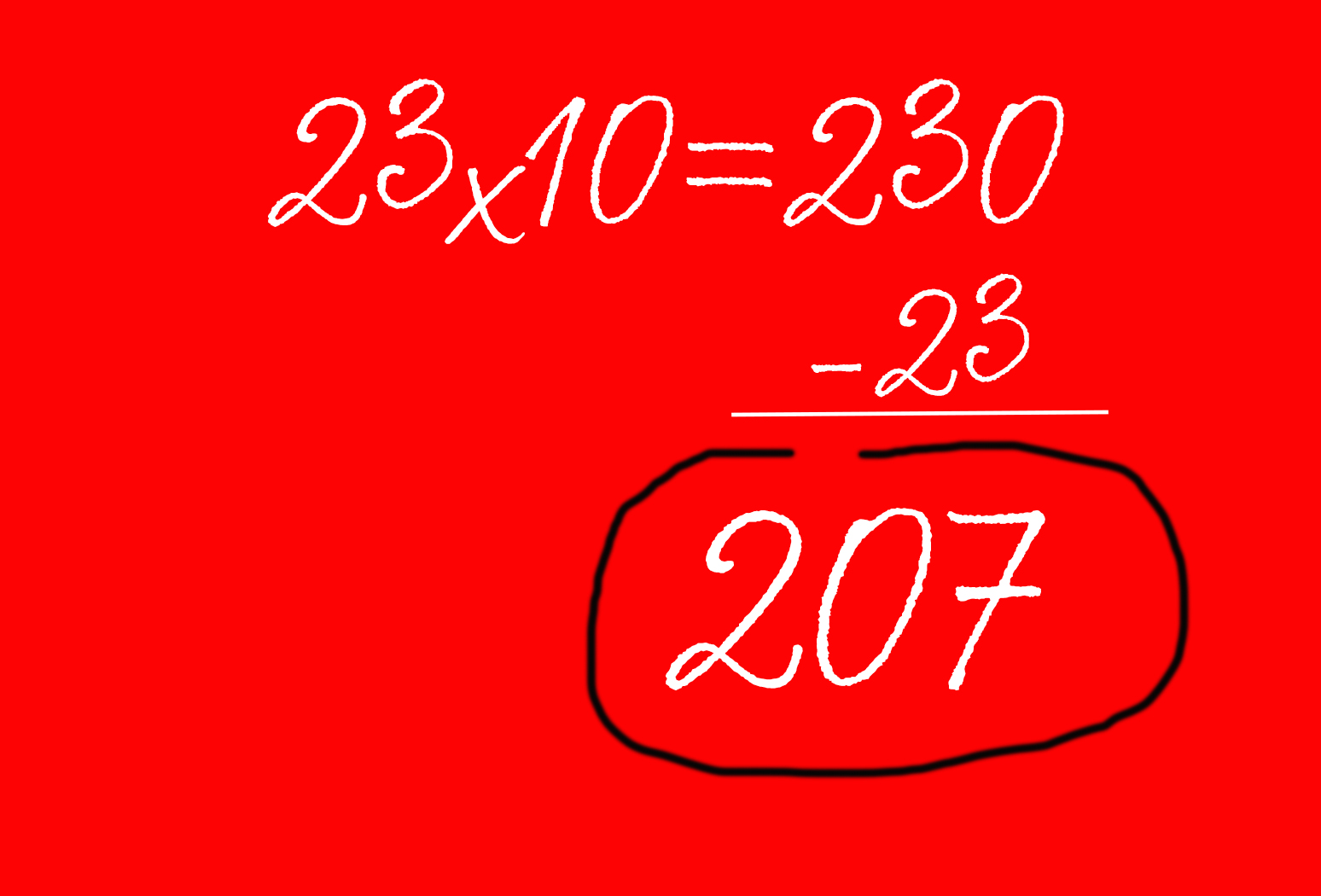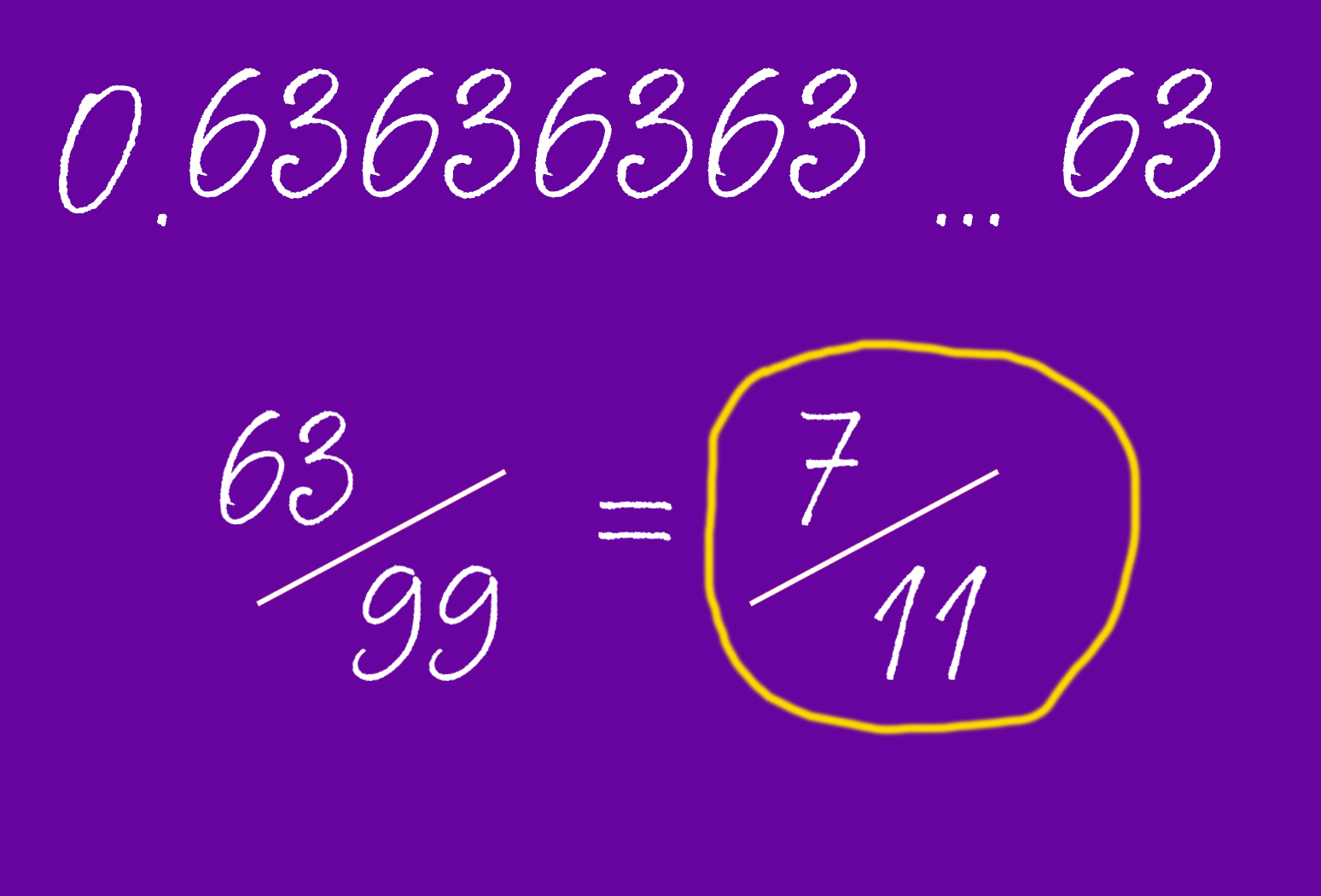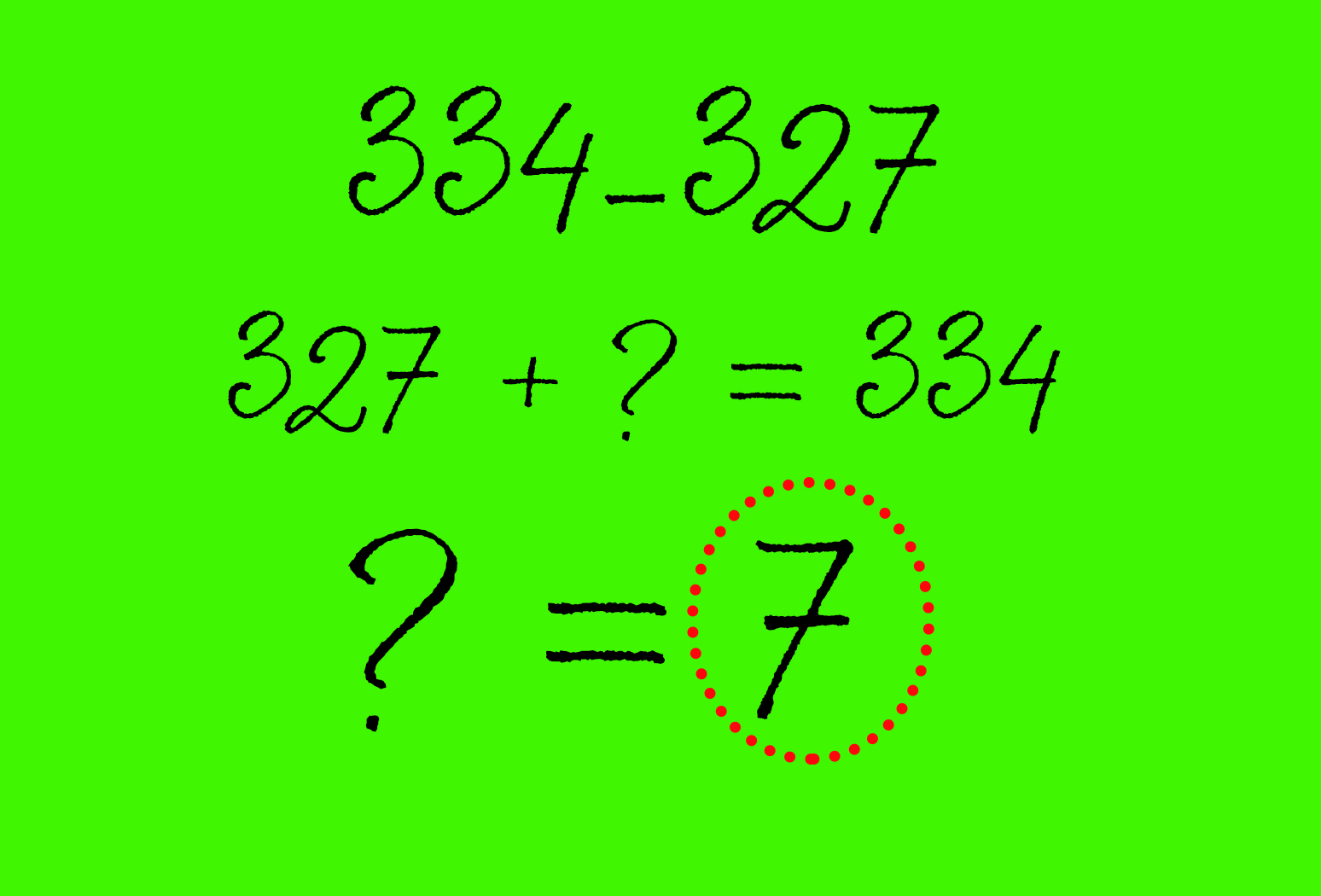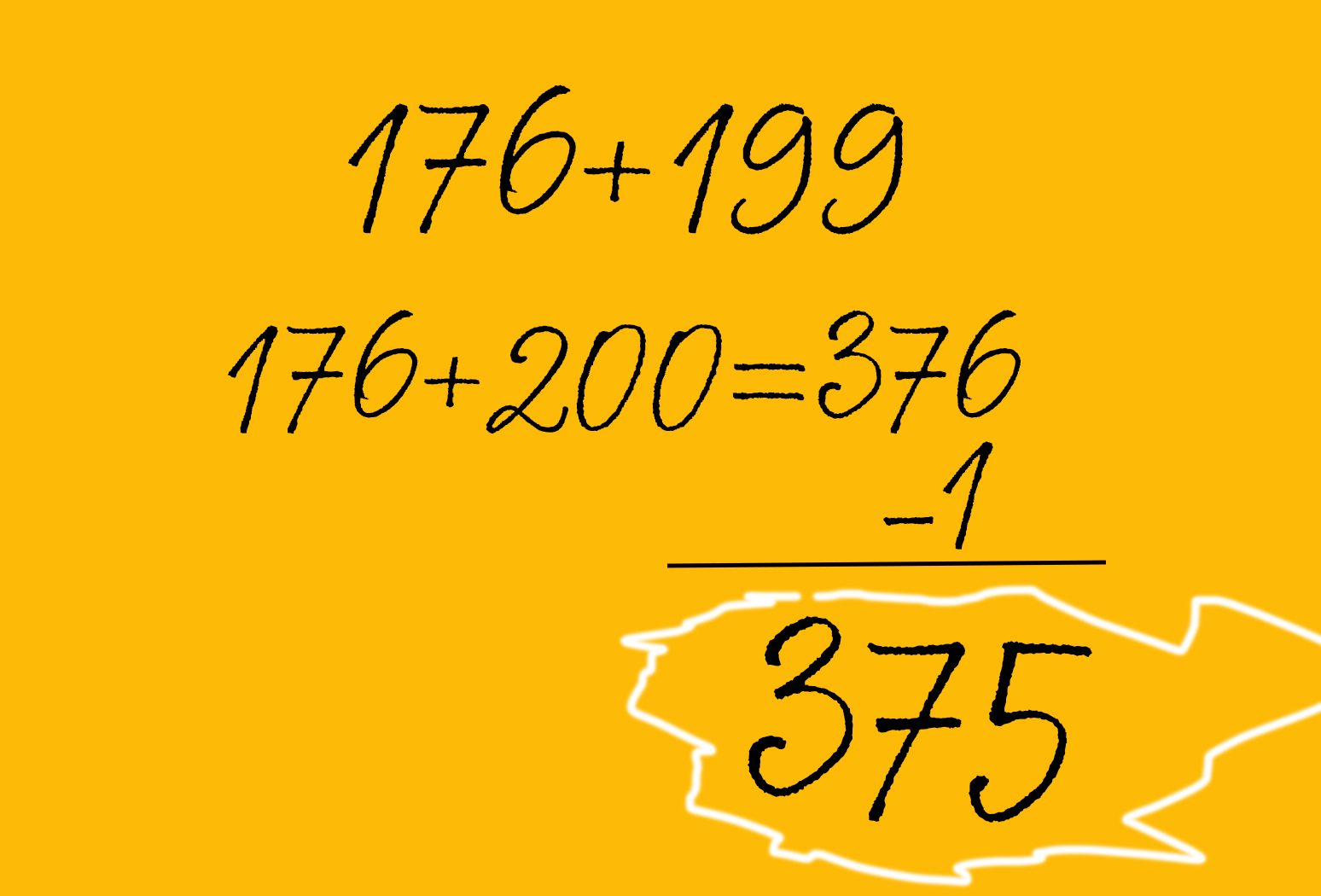быстрый счет в уме калькулятор в уме
Красота чисел. Как быстро вычислять в уме

Старинная запись на квитанции в уплате подати («ясака»). Она означает сумму 1232 руб. 24 коп. Иллюстрация из книги: Яков Перельман «Занимательная арифметика»
Ещё Ричард Фейнман в книге «Вы конечно шутите, мистер Фейнман!» поведал несколько приёмов устного счёта. Хотя это очень простые трюки, они не всегда входят в школьную программу.
Например, чтобы быстро возвести в квадрат число X около 50 (50 2 = 2500), нужно вычитать/прибавлять по сотне на каждую единицы разницы между 50 и X, а потом добавить разницу в квадрате. Описание звучит гораздо сложнее, чем реальное вычисление.
52 2 = 2500 + 200 + 4
47 2 = 2500 – 300 + 9
58 2 = 2500 + 800 + 64
Молодого Фейнмана научил этому трюку коллега-физик Ханс Бете, тоже работавший в то время в Лос-Аламосе над Манхэттенским проектом.
Ханс показал ещё несколько приёмов, которые использовал для быстрых вычислений. Например, для вычисления кубических корней и возведения в степень удобно помнить таблицу логарифмов. Это знание очень упрощает сложные арифметические операции. Например, вычислить в уме примерное значение кубического корня из 2,5. Фактически, при таких вычислениях в голове у вас работает своеобразная логарифмическая линейка, в которой умножение и деление чисел заменяется сложением и вычитанием их логарифмов. Удобнейшая вещь.

Логарифмическая линейка
До появления компьютеров и калькуляторов логарифмическую линейку использовали повсеместно. Это своеобразный аналоговый «компьютер», позволяющий выполнить несколько математических операций, в том числе умножение и деление чисел, возведение в квадрат и куб, вычисление квадратных и кубических корней, вычисление логарифмов, потенцирование, вычисление тригонометрических и гиперболических функций и некоторые другие операции. Если разбить вычисление на три действия, то с помощью логарифмической линейки можно возводить числа в любую действительную степень и извлекать корень любой действительной степени. Точность расчётов — около 3 значащих цифр.
Чтобы быстро проводить в уме сложные расчёты даже без логарифмической линейки, неплохо запомнить квадраты всех чисел, хотя бы до 25, просто потому что они часто используются в расчётах. И таблицу степеней — самых распространённых. Проще запомнить, чем вычислять каждый раз заново, что 5 4 = 625, 3 5 = 243, 2 20 = 1 048 576, а √3 ≈ 1,732.
Ричард Фейнман совершенствовал свои навыки и постепенно замечал всё новые интересные закономерности и связи между числами. Он приводит такой пример: «Если кто-то начинал делить 1 на 1,73, можно было незамедлительно ответить, что это будет 0,577, потому что 1,73 — это число, близкое к квадратному корню из трёх. Таким образом, 1/1,73 — это около одной трети квадратного корня из 3».
Настолько продвинутый устный счёт мог бы удивить коллег в те времена, когда не было компьютеров и калькуляторов. В те времена абсолютно все учёные умели хорошо считать в уме, поэтому для достижения мастерства требовалось достаточно глубоко погрузиться в мир цифр.
В наше время люди достают калькулятор, чтобы просто поделить 76 на 3. Удивить окружающих стало гораздо проще. Во времена Фейнмана вместо калькулятора были деревянные счёты, на которых тоже можно было производить сложные операции, в том числе брать кубические корни. Великий физик уже тогда заметил, что использование таких инструментов, людям вообще не нужно запоминать множество арифметический комбинаций, а достаточно просто научиться правильно катать шарики. То есть люди с «расширителями» мозга не знают чисел. Они хуже справляются с задачами в «автономном» режиме.
Вот пять очень простых советов устного счёта, которые рекомендует Яков Перельман в методичке «Быстрый счёт» 1941 года издательства.
1. Если одно из умножаемых чисел разлагается на множители, удобно бывает последовательно умножать на них.
225 × 6 = 225 × 2 × 3 = 450 × 3
147 × 8 = 147 × 2 × 2 × 2, то есть трижды удвоить результат
2. При умножении на 4 достаточно дважды удвоить результат. Аналогично, при делении на 4 и 8, число делится пополам дважды или трижды.
3. При умножении на 5 или 25 число можно разделить на 2 или 4, а затем приписать к результату один или два нуля.
Здесь лучше сразу оценивать, как проще. Например, 31 × 25 удобнее умножать как 25 × 31 стандартным способом, то есть как 750+25, а не как 31 × 25, то есть 7,75 × 100.
При умножении на число, близкое к круглому (98, 103), удобно сразу умножить на круглое число (100), а затем вычесть/прибавить произведение разницы.
37 × 98 = 3700 – 74
37 × 104 = 3700 + 148
4. Чтобы возвести в квадрат число, оканчивающееся цифрой 5 (например, 85), умножают число десятков (8) на него же плюс единица (9), и приписывают 25.
8 × 9 = 72, приписываем 25, так что 85 2 = 7225
Почему действует это правило, видно из формулы:
(10Х + 5) 2 = 100Х 2 + 100Х + 25 = 100Х (X+1) + 25
Приём применяется и к десятичным дробям, которые оканчиваются на 5:
5. При возведении в квадрат не забываем об удобной формуле
(a + b) 2 = a 2 + b 2 + 2ab
44 2 = 1600 + 16 + 320
Долой калькулятор: 12 простых трюков, которые помогут вам быстро считать
Просто, как дважды два.
Как бы мы ни хотели это признавать, учителя были правы: математика нужна каждому из нас. Но далеко не всем дается ловкое жонглирование числами. Тогда на помощь приходят легко запоминающиеся математические приемы – настоящее спасение, когда под рукой, как назло, нет калькулятора.
Ниже вы найдете 12 способов быстрых вычислений для всех, кто далек от точных наук.
1. Быстрое вычисление 20%
Представим, что границы вновь открыли и первым делом вы отправились в США. А там принято оставлять на чай. Обычно размер чаевых составляет 15-20% от суммы вашего заказа.
По словам Кейт Сноу, автора серии книг The Math Facts That Stick, чтобы быстро вычислить 20% от суммы, вам нужно просто разделить число в чеке на 5.
Например, вы поели на 85 долларов. Разделите 85 на 5, и у вас получится 17 долларов – чаевые, которые вы должны оставить официанту.
2. Умножение двузначных чисел на 11
Умножить число на 11 очень легко с помощью хитрого трюка от math.hmc.edu. Просто сложите две цифры и поместите полученную сумму в середину числа.
Например, вы умножаете 25 на 11. Если сложить 2 и 5, получится 7. Теперь расположите 7 между 2 и 5, чтобы найти окончательный ответ – 275.
3. Быстрое удвоение
Чтобы удвоить большое число, умножьте каждую цифру на 2 и сложите их между собой. Кейт Сноу предлагает начинать слева – так будет легче.
«Чтобы удвоить, к примеру, 147, начните с разряда сотен. Если умножить 100 на 2, получится 200. 40 на 2 – 80. 7 на 2 – 14. Теперь сложите числа между собой (200 + 80 + 14), и вы получите 294», – объясняет Сноу.
4. Умножение чисел, которые оканчиваются на ноль
Примеры с большими пугающими числами, которые оканчиваются на ноль, тоже легко решить с помощью специального приема. Согласно education.cu-portland.edu, нужно просто «вычеркнуть» нули из примера, а в конце вновь их добавить.
Если вы умножаете 600 на 400, уберите все нули и перемножьте 6 на 4. Получится 24. Затем подсчитайте общее количество нулей в исходном уравнении и припишите их к полученному значению. Так как в нашем примере было четыре нуля, то ответ будет равен 240000.
5. Умножение на 9
Если вам так и не удалось выучить таблицу умножения – не переживайте. По словам Сноу, чтобы легко умножить число на 9, нужно умножить его на 10 и вычесть исходное число из полученного значения.
Например, вам нужно умножить 9 на 23. Для этого умножаем 23 на 10 и получаем 230. А затем вычитаем из него 23, чтобы получить окончательный ответ – 207.
6. Деление на 10, 100 или 1000
Разделить число на 10 проще простого – согласно Сноу, «нужно просто переместить десятичный знак на одну позицию влево от исходного числа, чтобы найти ответ».
Для деления на 100 применим тот же метод, за исключением одного – нужно переместить десятичный разряд на две позиции левее исходного числа. Что касается деления на 1000, просто переместите десятичный знак на три позиции влево.
Например, если вы делите 42,94 на 10, вы просто перемещаете десятичный знак на одну позицию влево и получаете 4,294.
7. Умножение на 10, 100 или 1000
Здесь все работает с точностью до наоборот. Чтобы умножить число на 10, переместите десятичный знак на одну позицию вправо. На 100 – на две позиции. На 1000 – на три позиции.
Например, если вам нужно умножить 366,78 на 100, передвиньте десятичный знак на две цифры вправо, чтобы получить ответ 36678.
8. Преобразование периодической десятичной дроби в обыкновенную
Согласно businessinsider.com, нужно выполнить всего 3 шага, чтобы легко превратить бесконечную десятичную дробь в обыкновенную, с числителем и знаменателем.
9. Умножение на 25
Умножать на 25 не так уж и сложно, если представлять число в виде дроби 100/4. В этом случае все, что вам нужно сделать, это разделить число на 4 и умножить на 100.
Например, вам нужно умножить 84 на 25. Сначала делим 84 на 4 – получаем 21, а потом умножаем значение выражения на 100. Ответ: 2100.
10. Возведение чисел, оканчивающихся на 5, в квадрат
«Этот математический трюк подразумевает 2 шага», – объясняет Сноу. Чтобы возвести в квадрат число, которое оканчивается на пять, возьмите первую цифру числа и умножьте ее на себя. После этого прибавьте к полученному результату первую цифру и припишите к ответу 25. Кружится голова? Разберем на примере.
Если вы умножаете 35 на 35, сначала умножьте 3 на 3 – получится 9, – и прибавьте 3 к ответу – получится 12. Теперь припишите 25 в конец найденного числа, и вы найдете окончательный ответ: 1225.
11. Вычитание путем сложения
Если вам кажется, что сложение немного проще, чем вычитание, этот трюк для вас. Когда вам нужно найти разность двух чисел, достаточно близких друг к другу, попробуйте решить пример с помощью сложения.
«Вместо того чтобы пытаться вычесть 327 из 334, представьте это в виде суммы: мол, сколько нужно добавить к 327, чтобы получить 334?» – объясняет Сноу.
12. Сложение чисел, оканчивающихся на 99
Если вы пытаетесь прикинуть, во сколько обойдутся продукты, стоимость которых заканчивается на 99, – калькулятор не нужен. Все, что необходимо сделать, – прибавить 100 вместо 99, а потом вычесть единицу.
Сноу объясняет этот процесс на примере 176 + 199 = 375. «Если к 176 мы прибавим 200, то получим 376, – говорит эксперт. – Поскольку вы добавили на единицу больше, чем вам нужно, вычтите ее из 376, чтобы найти правильный ответ: 375».
Как быстро считать в уме: приемы устного счета больших чисел
Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.
Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.
После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).
Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.
Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.
Гаусс и устный счет

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.
По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.
В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.
Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.
Сложение чисел в уме
Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.
Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.
Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14
Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.
Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:
356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084
Вычитание чисел в уме
Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.
Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.
Теперь считаем: 528-300-20-1=228-20-1=208-1=207
Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.
Умножение чисел в уме
Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.
Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.
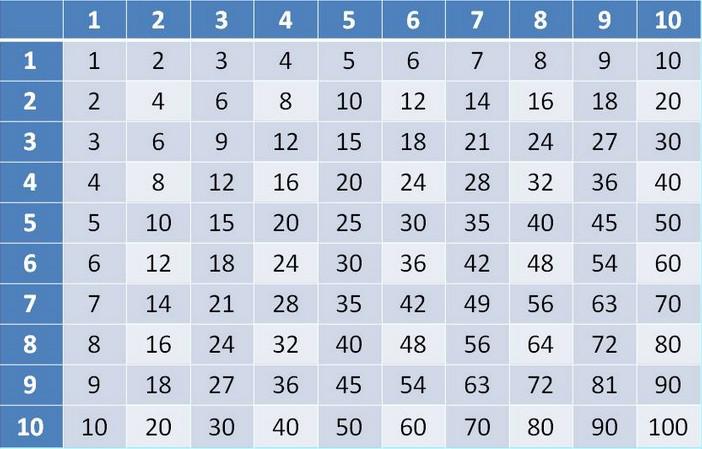
Умножение многозначных чисел на однозначные
Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.
528=500+20+8
528*6=500*6+20*6+8*6=3000+120+48=3168
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Умножение двузначных чисел
Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.
Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2
28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896
Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.
Умножение на 11
Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.
Проверим и умножим 54 на 11.
Возведение в квадрат
С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.
Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.
Проверим! Возведем в квадрат число 75.

Деление чисел в уме
Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.
Деление на однозначное число
При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.
Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:
6144:8=(5600+544):8=700+544:8
Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:
544:8=(480+64):8=60+64:8
Осталось разделить 64 на 8 и получить результат, сложив все результаты деления
6144:8=700+60+8=768
Деление на двузначное число
При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.
При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.
Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.
Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.
Сколько будет 4424:56?
Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.
56*80=4480
Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:
79*56=4424
Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Полезные советы
В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:
Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Эффективный счёт в уме или разминка для мозга
Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С.А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:
Используем круглые числа
Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:
Т.к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10. Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»: 1800 + 200 + 190.
Еще пример:
Упростим умножение делением
При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):
Аналогично выполняется умножение или деление на 25, ведь 25 = 100:4. Например,
Теперь не кажется невозможным умножить в уме 625 на 53:
Возведение в квадрат двузначного числа
Оказывается, чтобы просто возвести любое двузначное число в квадрат, достаточно запомнить квадраты всех чисел от 1 до 25. Благо, квадраты до 10 мы уже знаем из таблицы умножения. Остальные квадраты можно посмотреть в нижеприведённой таблице:
Приём Рачинского заключается в следующем. Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю. Например,
В общем случае (M — двузначное число):
Попробуем применить данный трюк при возведении в квадрат трёхзначного числа, разбив его предварительно на более мелкие слагаемые:
Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.
Умножение двузначных чисел
Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:
Составив их произведение, получим:
Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77.
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77. Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:
У этого приёма есть частный случай: всё значительно упрощается, когда у двух сомножителей одинаковое число десятков. В этом случае число десятков умножается на следующее за ним число и к полученному результату приписывается произведение единиц этих чисел. Посмотрим, как элегантен этот приём на примере.
48 x 42. Число десятков 4, последующее число: 5; 4 x 5 = 20. Произведение единиц: 8 x 2 = 16. Значит,
99 x 91. Число десятков: 9, последующее число: 10; 9 x 10 = 90. Произведение единиц: 9 x 1 = 09. Значит,
Ага, то есть, чтобы перемножить 95 x 95, достаточно посчитать 9 x 10 = 90 и 5 x 5 = 25 и ответ готов:
Тогда предыдущий пример можно вычислить немного проще:
Вместо заключения
Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.
Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».