что такое линейная регрессия в машинном обучении

Линейная регрессия для машинного обучения

Дата публикации 2016-03-25

Линейная регрессия является, пожалуй, одним из самых известных и понятных алгоритмов в статистике и машинном обучении.

В этой статье вы узнаете об алгоритме линейной регрессии, о том, как он работает и как вы можете наилучшим образом использовать его в своих проектах машинного обучения. В этом посте вы узнаете:

Вам не нужно знать какую-либо статистику или линейную алгебру, чтобы понять линейную регрессию. Это мягкое введение в технику высокого уровня, чтобы дать вам достаточно знаний, чтобы иметь возможность эффективно использовать ее в своих собственных задачах.

Разве линейная регрессия не из статистики?

Прежде чем мы углубимся в детали линейной регрессии, вы можете спросить себя, почему мы смотрим на этот алгоритм.

Разве это не техника из статистики?

Машинное обучение, в частности область прогнозного моделирования, в первую очередь связано с минимизацией ошибки модели или созданием максимально точных прогнозов за счет объяснимости. В прикладном машинном обучении мы будем заимствовать, повторно использовать и красть алгоритмы из множества различных областей, включая статистику, и использовать их для этих целей.

Как таковая, линейная регрессия была разработана в области статистики и изучается как модель для понимания взаимосвязи между входными и выходными числовыми переменными, но была заимствована машинным обучением. Это и статистический алгоритм, и алгоритм машинного обучения.

Далее, давайте рассмотрим некоторые распространенные имена, используемые для обозначения модели линейной регрессии.

Получите БЕСПЛАТНУЮ карту алгоритмов Mind

Я создал удобную карту разума из 60+ алгоритмов, организованных по типу.

Загрузите его, распечатайте и используйте.

Также получите эксклюзивный доступ к алгоритмам машинного обучения по электронной почте мини-курса.

Многие имена линейной регрессии

Когда вы начинаете изучать линейную регрессию, все может стать очень запутанным.

Причина в том, что линейная регрессия существовала так долго (более 200 лет). Он изучался со всех возможных сторон, и часто каждый угол имеет новое и другое имя.

Линейная регрессия являетсялинейная модельнапример, модель, которая предполагает линейную связь между входными переменными (x) и единственной выходной переменной (y). Более конкретно, что у можно вычислить из линейной комбинации входных переменных (х).

Когда есть одна входная переменная (x), метод называетсяпростая линейная регрессия, Когда естьнесколько входных переменныхВ литературе из статистики часто упоминается метод как множественная линейная регрессия.

Различные методы могут быть использованы для подготовки или обучения уравнения линейной регрессии из данных, наиболее распространенный из которых называетсяОбычные наименьшие квадраты, Поэтому принято называть модель, подготовленную таким образом, линейной регрессией наименьших квадратов или регрессией наименьших квадратов.

Теперь, когда мы знаем некоторые имена, используемые для описания линейной регрессии, давайте подробнее рассмотрим используемое представление.

Представление модели линейной регрессии

Линейная регрессияэто привлекательная модель, потому что представление так просто.

Представление представляет собой линейное уравнение, которое объединяет определенный набор входных значений (x), решением которого является прогнозируемый выходной сигнал для этого набора входных значений (y). Таким образом, и входные значения (x), и выходные значения являются числовыми.

Линейное уравнение присваивает один масштабный коэффициент каждому входному значению или столбцу, который называется коэффициентом и представлен заглавной греческой буквой Beta (B). Также добавляется один дополнительный коэффициент, дающий линии дополнительную степень свободы (например, перемещение вверх и вниз на двумерном графике), и его часто называют коэффициентом пересечения или смещения.

Например, в простой задаче регрессии (один x и один y) форма модели будет иметь вид:

В более высоких измерениях, когда у нас более одного входа (x), линия называется плоскостью или гиперплоскостью. Следовательно, представление представляет собой форму уравнения и конкретные значения, используемые для коэффициентов (например, B0 и B1 в вышеприведенном примере).

Часто говорят о сложности регрессионной модели, такой как линейная регрессия. Это относится к количеству коэффициентов, используемых в модели.

Когда коэффициент становится равным нулю, он эффективно устраняет влияние входной переменной на модель и, следовательно, на прогноз, сделанный из модели (0 * x = 0) Это становится актуальным, если вы посмотрите на методы регуляризации, которые изменяют алгоритм обучения, чтобы уменьшить сложность регрессионных моделей, оказывая давление на абсолютный размер коэффициентов, приводя некоторые к нулю.

Теперь, когда мы понимаем представление, используемое для модели линейной регрессии, давайте рассмотрим некоторые способы, которыми мы можем изучить это представление на основе данных.

Линейная регрессия, обучение модели

Изучение модели линейной регрессии означает оценку значений коэффициентов, используемых в представлении, с использованием имеющихся у нас данных.

В этом разделе мы кратко рассмотрим четыре метода для подготовки модели линейной регрессии. Этой информации недостаточно, чтобы реализовать их с нуля, но достаточно, чтобы понять особенности вычислений и компромиссов.

Есть много других методов, потому что модель так хорошо изучена. Обратите внимание на обычные наименьшие квадраты, потому что это наиболее распространенный метод, используемый в целом. Также обратите внимание на Gradient Descent, так как это наиболее распространенный метод обучения на уроках машинного обучения.

1. Простая линейная регрессия

С помощью простой линейной регрессии, когда у нас есть один вход, мы можем использовать статистику для оценки коэффициентов.

Для этого необходимо рассчитать статистические свойства из данных, таких как средние значения, стандартные отклонения, корреляции и ковариация. Все данные должны быть доступны для просмотра и расчета статистики.

Это весело как упражнение в Excel, но не очень полезно на практике.

2. Обычные наименьшие квадраты

Когда у нас есть более одного входа, мы можем использовать Обыкновенные наименьшие квадраты для оценки значений коэффициентов.

Обычные наименьшие квадратыПроцедура стремится минимизировать сумму квадратов невязок. Это означает, что, учитывая линию регрессии через данные, мы вычисляем расстояние от каждой точки данных до линии регрессии, возводим ее в квадрат и суммируем все квадратные ошибки вместе. Это количество, которое обычные наименьшие квадраты стремятся минимизировать.

Этот подход обрабатывает данные как матрицу и использует операции линейной алгебры для оценки оптимальных значений для коэффициентов. Это означает, что все данные должны быть доступны, и у вас должно быть достаточно памяти для размещения данных и выполнения матричных операций.

Необычно реализовать процедуру Обыкновенных наименьших квадратов самостоятельно, разве что как упражнение по линейной алгебре. Скорее всего, вы вызовете процедуру в библиотеке линейной алгебры. Эта процедура очень быстро рассчитывается.

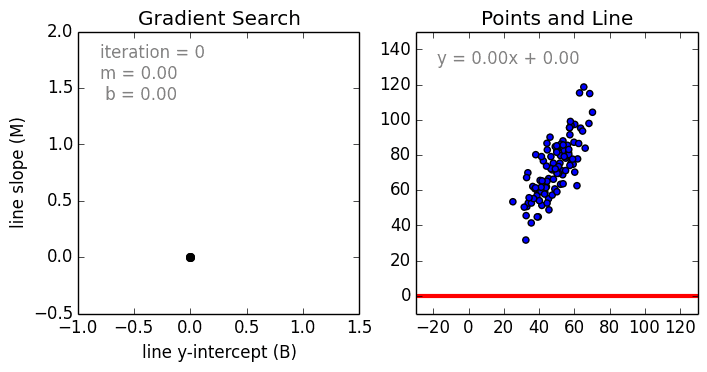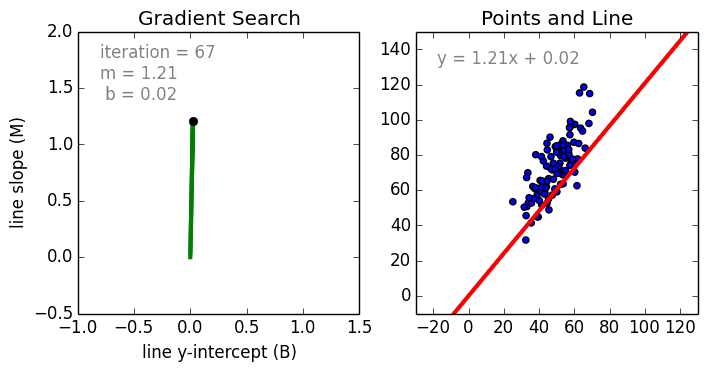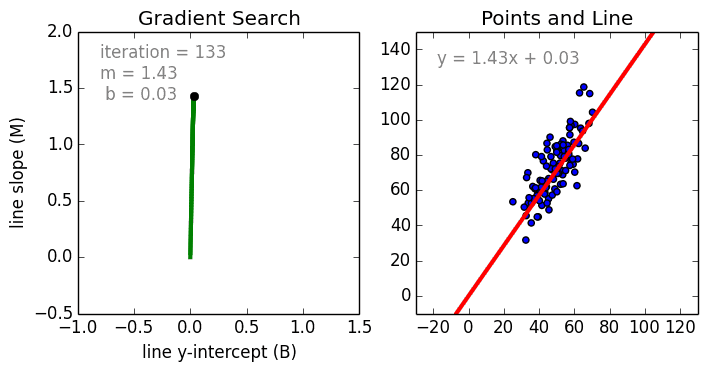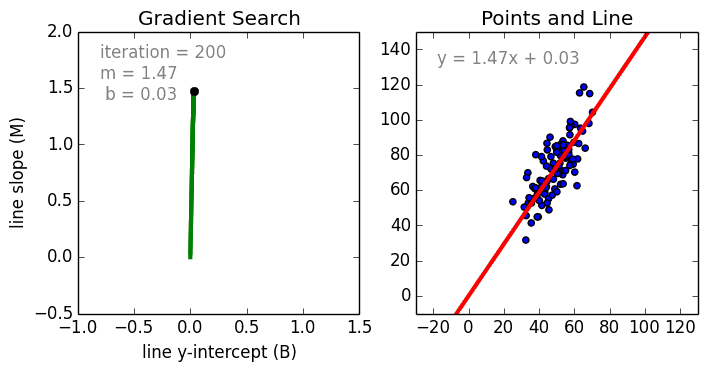
3. Градиентный спуск

При наличии одного или нескольких входных данных вы можете использовать процесс оптимизации значений коэффициентов путем итеративной минимизации ошибки модели в ваших данных обучения.

Эта операция называетсяГрадиентный спуски работает, начиная со случайных значений для каждого коэффициента. Сумма квадратов ошибок рассчитывается для каждой пары входных и выходных значений. Скорость обучения используется в качестве масштабного коэффициента, а коэффициенты обновляются в направлении минимизации ошибки. Процесс повторяется до тех пор, пока не будет достигнута минимальная квадратичная ошибка или дальнейшее улучшение невозможно.

При использовании этого метода необходимо выбрать параметр скорости обучения (альфа), который определяет размер шага улучшения, который будет выполняться на каждой итерации процедуры.

Градиентный спуск часто преподается с использованием модели линейной регрессии, потому что это относительно просто для понимания. На практике это полезно, когда у вас очень большой набор данных по количеству строк или столбцам, которые могут не помещаться в памяти.

4. Регуляризация

Два популярных примера процедур регуляризации для линейной регрессии:

Эти методы эффективны для использования, когда во входных значениях есть коллинеарность, и обычные наименьшие квадраты будут соответствовать обучающим данным.

Теперь, когда вы знаете некоторые методы для изучения коэффициентов в модели линейной регрессии, давайте посмотрим, как мы можем использовать модель для прогнозирования новых данных.

Прогнозирование с помощью линейной регрессии

Учитывая, что представление представляет собой линейное уравнение, делать предсказания так же просто, как решить уравнение для определенного набора входных данных.

Давайте сделаем это на примере. Представьте, что мы предсказываем вес (у) от роста (х) Наше представление модели линейной регрессии для этой задачи будет:

Например, давайте использовать B0 = 0,1 и B1 = 0,5. Давайте подключим их и посчитаем вес (в килограммах) для человека ростом 182 сантиметра.

Вы можете видеть, что приведенное выше уравнение может быть построено в виде линии в двух измерениях. B0 является нашей отправной точкой независимо от того, какая у нас высота. Мы можем пробегать кучу высот от 100 до 250 сантиметров и подключать их к уравнению и получать значения веса, создавая нашу линию.

Теперь, когда мы знаем, как делать прогнозы на основе усвоенной модели линейной регрессии, давайте рассмотрим некоторые практические правила подготовки наших данных для максимально эффективного использования модели этого типа.

Подготовка данных для линейной регрессии

Линейная регрессия изучалась очень долго, и существует много литературы о том, как ваши данные должны быть структурированы, чтобы наилучшим образом использовать модель.

Таким образом, при рассмотрении этих требований и ожиданий возникает много изощренности, которая может быть пугающей. На практике вы можете больше использовать эти правила в качестве практических правил при использовании Регрессии обыкновенных наименьших квадратов, наиболее распространенной реализации линейной регрессии.

Попробуйте разные методы подготовки ваших данных, используя эту эвристику, и посмотрите, что лучше всего подходит для вашей проблемы.

УвидетьСтатья в Википедии о линейной регрессиидля превосходного списка предположений, сделанных моделью. Существует также большой список предположений оОбыкновенная статья Википедии «Наименьшие квадраты»,

Дальнейшее чтение

Есть еще много чего почитать о линейной регрессии. Начните использовать его, прежде чем приступить к чтению, но если вы хотите погрузиться глубже, ниже приведены некоторые ссылки, которые вы можете использовать.

Книги машинного обучения, в которых упоминается линейная регрессия

Это некоторые книги по машинному обучению, которые вы можете иметь или иметь к ним доступ, которые описывают линейную регрессию в контексте машинного обучения.

Сообщения о линейной регрессии

Ниже приведены некоторые интересные очерки и сообщения в блоге о линейной регрессии, с которыми я столкнулся.

Знаете еще какие-нибудь хорошие ссылки на линейную регрессию с наклонностью к машинному обучению и прогнозному моделированию? Оставьте комментарий и дайте мне знать.

Резюме

В этом посте вы обнаружили алгоритм линейной регрессии для машинного обучения.

Вы преодолели много вопросов, в том числе:

Попробуйте линейную регрессию и освоитесь с ней

У вас есть вопросы о линейной регрессии или об этом посте?
Оставьте комментарий и спросите, я сделаю все возможное, чтобы ответить.

Источник

Линейная регрессия на Python: объясняем на пальцах

Линейная регрессия применяется для анализа данных и в машинном обучении. Постройте свою модель на Python и получите первые результаты!

Что такое регрессия?

Регрессия ищет отношения между переменными.

Для примера можно взять сотрудников какой-нибудь компании и понять, как значение зарплаты зависит от других данных, таких как опыт работы, уровень образования, роль, город, в котором они работают, и так далее.

Регрессия решает проблему единого представления данных анализа для каждого работника. Причём опыт, образование, роль и город – это независимые переменные при зависимой от них зарплате.

Таким же способом можно установить математическую зависимость между ценами домов в определённой области, количеством комнат, расстоянием от центра и т. д.

Регрессия рассматривает некоторое явление и ряд наблюдений. Каждое наблюдение имеет две и более переменных. Предполагая, что одна переменная зависит от других, вы пытаетесь построить отношения между ними.

Другими словами, вам нужно найти функцию, которая отображает зависимость одних переменных или данных от других.

Зависимые данные называются зависимыми переменными, выходами или ответами.

Независимые данные называются независимыми переменными, входами или предсказателями.

Обычно в регрессии присутствует одна непрерывная и неограниченная зависимая переменная. Входные переменные могут быть неограниченными, дискретными или категорическими данными, такими как пол, национальность, бренд, etc.

Когда вам нужна регрессия?

Регрессия полезна для прогнозирования ответа на новые условия. Можно угадать потребление электроэнергии в жилом доме из данных температуры, времени суток и количества жильцов.

Где она вообще нужна?

Регрессия используется во многих отраслях: экономика, компьютерные и социальные науки, прочее. Её важность растёт с доступностью больших данных.

Линейная регрессия

Линейная регрессия – одна из важнейших и широко используемых техник регрессии. Эта самый простой метод регрессии. Одним из его достоинств является лёгкость интерпретации результатов.

Постановка проблемы

Линейная регрессия некоторой зависимой переменной y на набор независимых переменных x = (x₁, …, xᵣ), где r – это число предсказателей, предполагает, что линейное отношение между y и x: y = 𝛽₀ + 𝛽₁x₁ + ⋯ + 𝛽ᵣxᵣ + 𝜀. Это уравнение регрессии. 𝛽₀, 𝛽₁, …, 𝛽ᵣ – коэффициенты регрессии, и 𝜀 – случайная ошибка.

Линейная регрессия вычисляет оценочные функции коэффициентов регрессии или просто прогнозируемые весы измерения, обозначаемые как b₀, b₁, …, bᵣ. Они определяют оценочную функцию регрессии f(x) = b₀ + b₁x₁ + ⋯ + bᵣxᵣ. Эта функция захватывает зависимости между входами и выходом достаточно хорошо.

Для каждого результата наблюдения i = 1, …, n, оценочный или предсказанный ответ f(xᵢ) должен быть как можно ближе к соответствующему фактическому ответу yᵢ. Разницы yᵢ − f(xᵢ) для всех результатов наблюдений называются остатками. Регрессия определяет лучшие прогнозируемые весы измерения, которые соответствуют наименьшим остаткам.

Для получения лучших весов, вам нужно минимизировать сумму остаточных квадратов (SSR) для всех результатов наблюдений: SSR = Σᵢ(yᵢ − f(xᵢ))². Этот подход называется методом наименьших квадратов.

Простая линейная регрессия

Простая или одномерная линейная регрессия – случай линейной регрессии с единственной независимой переменной x.

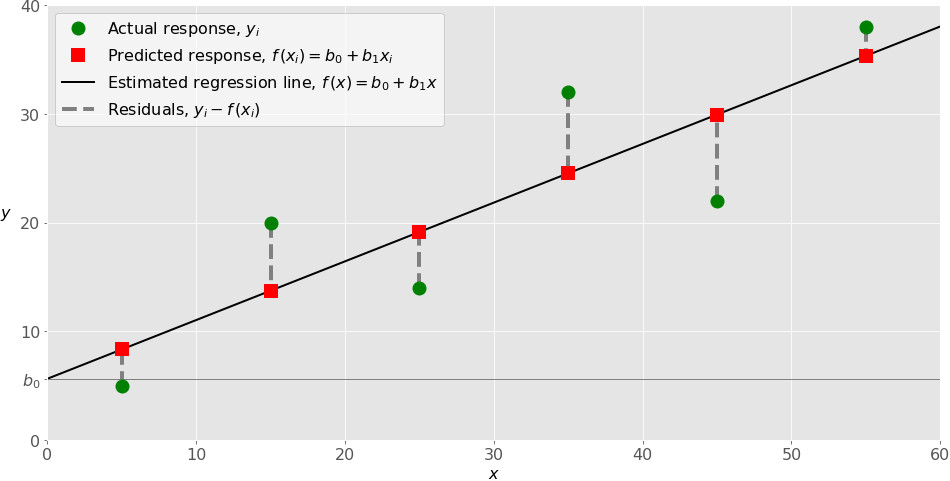
Реализация простой линейной регрессии начинается с заданным набором пар (зелёные круги) входов-выходов (x-y). Эти пары – результаты наблюдений. Наблюдение, крайнее слева (зелёный круг) имеет на входе x = 5 и соответствующий выход (ответ) y = 5. Следующее наблюдение имеет x = 15 и y = 20, и так далее.

Оценочная функция регрессии (чёрная линия) выражается уравнением f(x) = b₀ + b₁x. Нужно рассчитать оптимальные значения спрогнозированных весов b₀ и b₁ для минимизации SSR и определить оценочную функцию регрессии. Величина b₀, также называемая отрезком, показывает точку, где расчётная линия регрессии пересекает ось y. Это значение расчётного ответа f(x) для x = 0. Величина b₁ определяет наклон расчетной линии регрессии.

Предсказанные ответы (красные квадраты) – точки линии регрессии, соответствующие входным значениям. Для входа x = 5 предсказанный ответ равен f(5) = 8.33 (представленный крайним левыми квадратом).

Остатки (вертикальные пунктирные серые линии) могут быть вычислены как yᵢ − f(xᵢ) = yᵢ − b₀ − b₁xᵢ для i = 1, …, n. Они представляют собой расстояния между зелёными и красными пунктами. При реализации линейной регрессии вы минимизируете эти расстояния и делаете красные квадраты как можно ближе к предопределённым зелёным кругам.

Реализуйте линейную регрессию в Python

Пришло время реализовать линейную регрессию в Python. Всё, что вам нужно, – подходящие пакеты, функции и классы.

Пакеты Python для линейной регрессии

NumPy – фундаментальный научный пакет для быстрых операций над одномерными и многомерными массивами. Он облегчает математическую рутину и, конечно, находится в open-source.

Незнакомы с NumPy? Начните с официального гайда.

Пакет scikit-learn – это библиотека, широко используемая в машинном обучении. Она предоставляет значения для данных предварительной обработки, уменьшает размерность, реализует регрессию, классификацию, кластеризацию и т. д. Находится в open-source, как и NumPy.

Начните знакомство с линейными моделями и работой пакета на сайте scikit-learn.

Простая линейная регрессия со scikit-learn

Начнём с простейшего случая линейной регрессии.

Следуйте пяти шагам реализации линейной регрессии:

Это общие шаги для большинства подходов и реализаций регрессии.

Шаг 1: Импортируйте пакеты и классы

Первым шагом импортируем пакет NumPy и класс LinearRegression из sklearn.linear_model :

Теперь у вас есть весь функционал для реализации линейной регрессии.

Класс sklearn.linear_model.LinearRegression используем для линейной регрессии и прогнозов.

Шаг 2 : Предоставьте данные

Вторым шагом определите данные, с которыми предстоит работать. Входы (регрессоры, x) и выход (предиктор, y) должны быть массивами (экземпляры класса numpy.ndarray ) или похожими объектами. Вот простейший способ предоставления данных регрессии:

Вот как x и y выглядят теперь:

Шаг 3: Создайте модель

На этом шаге создайте и приспособьте модель линейной регрессии к существующим данным.

Наш пример использует состояния параметров по умолчанию.

Эта операция короче и делает то же, что и две предыдущие.

Шаг 4: Получите результаты

После совмещения модели нужно убедиться в удовлетворительности результатов для интерпретации.

.score() принимает в качестве аргументов предсказатель x и регрессор y, и возвращает значение R².

Примерное значение b₀ = 5.63 показывает, что ваша модель предсказывает ответ 5.63 при x, равном нулю. Равенство b₁ = 0.54 означает, что предсказанный ответ возрастает до 0.54 при x, увеличенным на единицу.

Заметьте, что вы можете предоставить y как двумерный массив. Тогда результаты не будут отличаться:

Шаг 5: Предскажите ответ

Когда вас устроит ваша модель, вы можете использовать её для прогнозов с текущими или другими данными.

Вот почти идентичный способ предсказать ответ:

В этом случае вы умножаете каждый элемент массива x с помощью model.coef_ и добавляете model.intercept_ в ваш продукт.

Вывод отличается от предыдущего примера количеством измерений. Теперь предсказанный ответ – это двумерный массив, в отличии от предыдущего случая, в котором он одномерный.

На практике модель регрессии часто используется для прогнозов. Это значит, что вы можете использовать приспособленные модели для вычисления выходов на базе других, новых входов:

О LinearRegression вы узнаете больше из официальной документации.

Теперь у вас есть своя модель линейной регрессии!

Источник

Регрессия в машинном обучении: оптимальный алгоритм

Регрессия используется в ML. Рассмотрим несколько алгоритмов и определим, как их использовать, исходя из преимуществ и недостатков.

Сталкиваясь с какой-либо проблемой в ML, помните, что есть множество алгоритмов, позволяющих её решить. Однако не существует такого универсального алгоритма, который подходил бы под все случаи и решал абсолютно все проблемы.

Выбор алгоритма строго зависит от размера и структуры ваших данных. Таким образом, выбор правильного алгоритма может быть неясен до тех пор, пока мы не проверим возможные варианты и не наткнёмся на ошибки.

Но каждый алгоритм обладает как преимуществами, так и недостатками, которые можно использовать в качестве руководства для выбора наиболее подходящего под ситуацию.

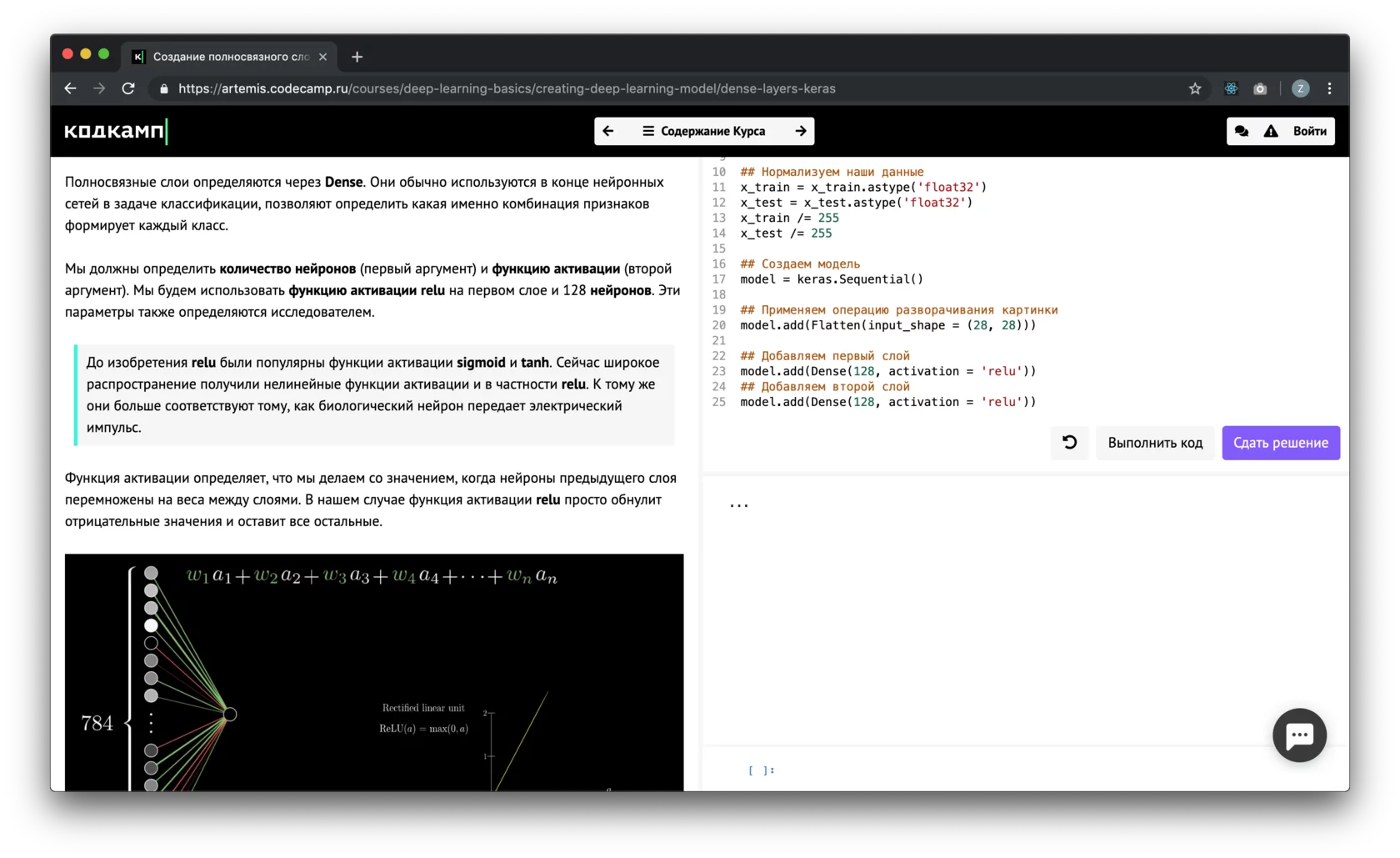
Линейная и полиномиальная регрессия

Начнём с простого. Одномерная (простая) линейная регрессия – это метод, используемый для моделирования отношений между одной независимой входной переменной (переменной функции) и выходной зависимой переменной. Модель линейная.

Более общий случай – множественная линейная регрессия, где создаётся модель взаимосвязи между несколькими входными переменными и выходной зависимой переменной. Модель остаётся линейной, поскольку выходное значение представляет собой линейную комбинацию входных значений.

Также стоит упомянуть полиномиальную регрессию. Модель становится нелинейной комбинацией входных переменных, т. е. среди них могут быть экспоненциальные переменные: синус, косинус и т. п. Модели регрессии можно обучить с помощью метода стохастического градиента.

Преимущества:

Недостатки:

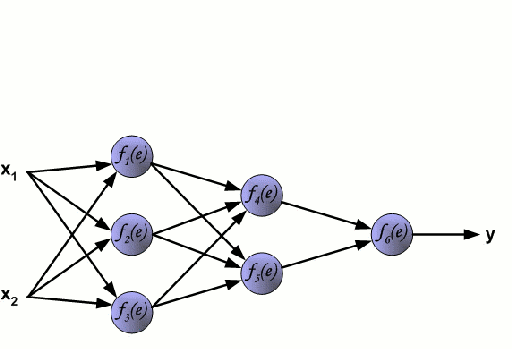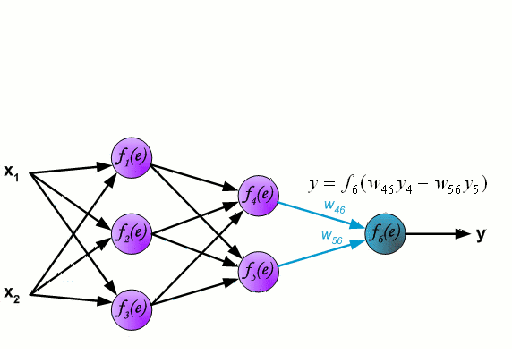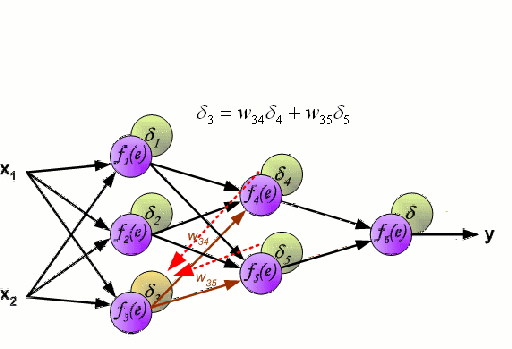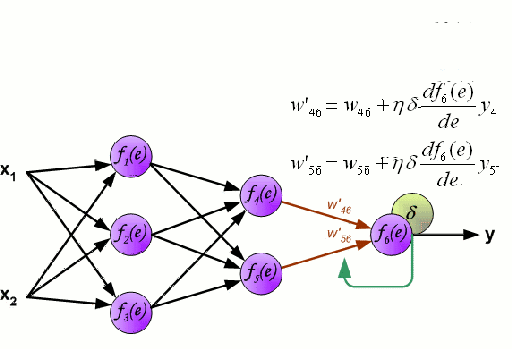
Нейронные сети

Нейронная сеть состоит из взаимосвязанных групп узлов, называемых нейронами. Входные данные передаются в эти нейроны в виде линейной комбинации со множеством переменных. Значение, умножаемое на каждую функциональную переменную, называется весом. Затем к этой линейной комбинации применяется нелинейность, что даёт нейронной сети возможность моделировать сложные нелинейные отношения. Чаще всего нейросети бывают многослойными: выход одного слоя передается следующему так, как описано выше. На выходе нелинейность не применяется.

Нейронные сети тренируются с помощью метода стохастического градиента и алгоритма обратного распространения ошибки.

Преимущества:

Недостатки:

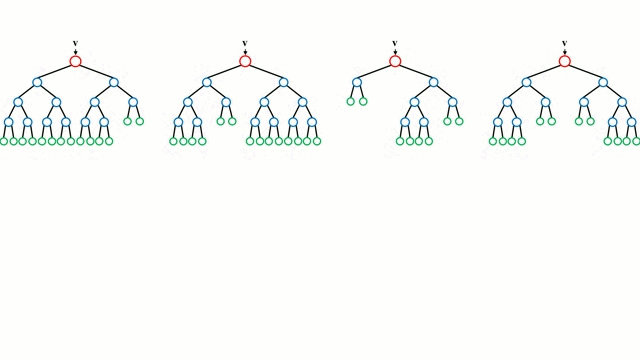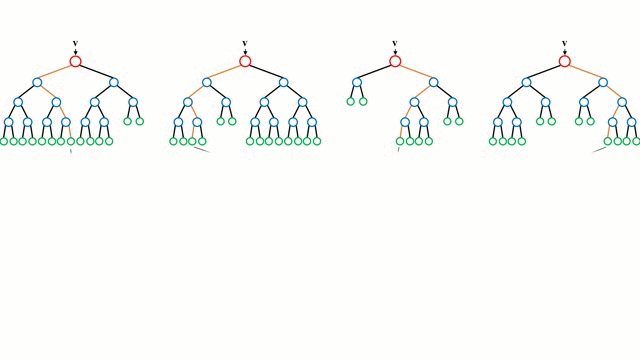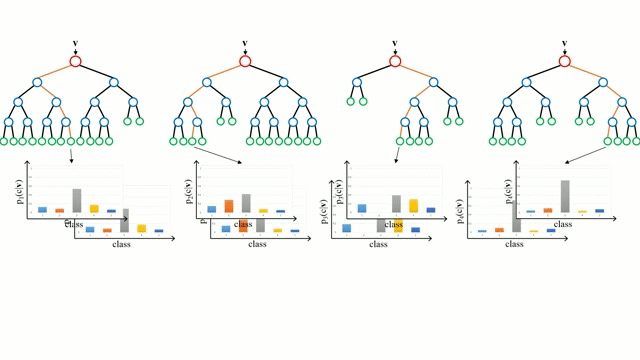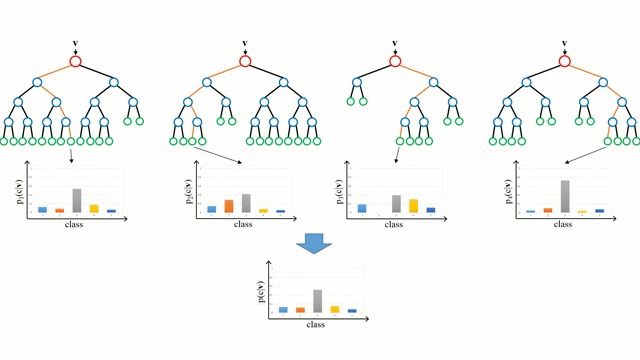
Дерево принятия решений и Случайный лес

Начнём с простого случая. Дерево принятия решений – это представления правил, находящихся в последовательной, иерархической структуре, где каждому объекту соответствует узел, дающий решение. При построении дерева важно классифицировать атрибуты так, чтобы создать “чистые” узлы. То есть выбранный атрибут должен разбить множество так, чтобы получаемые в итоге подмножества состояли из объектов, принадлежащих к одному классу, или были максимально приближены к этому, т.е. количество объектов из других классов в каждом из этих множеств было как можно меньше.

“Случайные лес” – совокупность деревьев принятия решений. Входной вектор проходит через несколько деревьев решений. Для регрессии выходное значение всех деревьев усредняется; для классификации используется схема голосования для определения конечного класса.

Источник

Введение в линейную регрессию для машинного обучения

Линейная регрессия, пожалуй, один из самых известных и хорошо понятных алгоритмов в статистике и машинном обучении.

В этом уроке вы откроете для себя алгоритм линейной регрессии, как он работает и как вы можете наилучшим образом использовать его в своих проектах машинного обучения. В этом уроке вы узнаете:

Почему линейная регрессия относится как к статистике, так и к машинному обучению.

Разве линейная регрессия происходит не от статистики?

Прежде чем мы погрузимся в детали линейной регрессии, вы можете спросить себя, почему мы смотрим на этот алгоритм.

Разве это не техника из статистики?

Машинное обучение, в частности, область прогнозного моделирования в первую очередь связана с минимизацией ошибки модели или созданием наиболее точных прогнозов, за счет объяснимости. При применении машинного обучения мы будем заимствовать, повторно использовать и «воровать» алгоритмы из разных областей, включая статистику, и использовать их в этих целях.

Таким образом, линейная регрессия была разработана в области статистики и изучается в качестве модели для понимания взаимосвязи между входными и выходными числовыми переменными, но заимствована машинным обучением. Это одного и статистический алгоритм, и алгоритм машинного обучения.

Далее рассмотрим некоторые из общих имен, используемых для обозначения модели линейной регрессии.

Многоликость линейной регрессии

Когда вы начинаете смотреть алгоритм линейной регрессии, все может казаться очень запутанным.

Алгоритм существует более 200 лет уже был изучен со всех возможных точек зрения и часто каждый новых угол имеет предназначение и другое название.

При наличии одной переменной ввода (x) метод называется простой линейной регрессией. Когда существует несколько переменных входных данных, литература из статистики часто называет метод множественной линейной регрессией.

Различные методы могут быть использованы для подготовки или обучения линейной регрессии. Наиболее распространенным из которых называется Метод наименьших квадратов (или сокращенно МНК, по-английски это Ordinary Least Squares или OLS).

Теперь, когда вы знаете некоторые названия, используемые для описания линейной регрессии, давайте подробнее рассмотрим используемое представление.

Представление модели линейной регрессии

Линейная регрессия является привлекательной моделью, потому что ее представление очень простое.

Линейное уравнение присваивает масштабный коэффициент (по-английски «scale factor») к каждому входному значению X. Масштабный коэффициент представлен греческой буквой Beta (B). Добавлен также один дополнительный коэффициент, добавляющую дополнительную степень свободы (например, движение вверх и вниз по двумерном участку) и часто называют коэффициентом перехвата или смещения (по-английски «bias coefficient»).

Наиболее простая задача регрессии когда на вход подается одна переменная X и есть одно выходящее значение Y. Форма подобной модели будет:

В случае многомерных измерений (т.е. когда у нас есть более одной вводной переменной (X)), линия превращается в плоскостью или гипер-плоскости. Таким образом, представление представляет собой форму уравнения и конкретные значения, используемые для коэффициентов (например, B0 и B1 в приведенном выше примере).

Когда конкретный элемент коэффициент Beta становится нулевым, он эффективно удаляет влияние входной переменной на модель и, следовательно, влияния на прогноз модели (0 * Xi = 0). Это становится актуальным, если вы применяете методы регуляризации (о них мы расскажем отдельно), которые изменяют алгоритм обучения, чтобы уменьшить сложность моделей регрессии, оказывая давление на абсолютный размер коэффициентов, приводя некоторые из них к нулю.

Теперь, когда мы понимаем что представление, используемое для модели линейной регрессии, давайте рассмотрим некоторые способы, с помощью которых мы можем узнать это представление из данных.

Методы линейной регрессии

Изучение модели линейной регрессии означает исследование получаемых значений коэффициентов, используемых в представлении, на основе имеющихся входных данных.

В этой части урока мы кратко рассмотрим четыре метода для подготовки модели для линейной регрессии. Это не достаточно информации для реализации их с нуля, но достаточно, чтобы получить первые впечатления и компромиссы при их вычислении.

Есть еще много методов, потому что модель линейной регрессии так хорошо изучены. Важно обратить внимание что на метод наименьших квадратов, потому что это наиболее распространенный метод, используемый в целом в индустрии для задач оптимизации. Также обратите внимание метод Градиентного спуска (по-английски Gradient descent), как наиболее распространенный метод применяемый в различных классах задач машинного обучения.

Простая линейная регрессия

При простой линейной регрессии, когда у нас есть один входной параметр, мы можем использовать статистику для оценки коэффициентов.

Для этого необходимо вычислить статистические свойства на таких данных, как среднее значение, стандартные отклонения, корреляции и ковариантность. Все данные должны быть доступны для обхода и расчета статистик.

Это весело, как упражнение полезно однажды проделать в Excel, но не очень полезно на практике.

Метод Наименьших Квадратов

Когда у нас есть более одной входной переменной, мы можем использовать метод наименьших квадратов для оценки значений коэффициентов.

Процедура наименьших квадратов направлена на минимизацию суммы квадратов остатков. Это означает, что, учитывая регрессионную линию через данные, мы вычисляем расстояние от каждой входной точки Xi до линии регрессии, берем квадрат этого расстояние и суммируем все квадраты подобных расстояний. Это количество, которое обычные наименее квадратов стремится свести к минимуму.

Такой подход рассматривает данные как матрицу и использует операции линейной алгебры для оценки оптимальных значений коэффициентов. Это означает, что все данные должны быть доступны, и вы должны иметь достаточно памяти, чтобы соответствовать размеру датасета и выполнять матричные операции.

Руками подобные вычисления уже давно никто не делает (кроме как для собственного понимания или в рамках домашнего задания в школе или ВУЗе). Вы просто вызываете процедуру из библиотеки линейной алгебры. Эта процедура умеет быстро вычислять подобные задачи.

Градиентный спуск

При наличии одной или нескольких переменных можно использовать процесс оптимизации значений коэффициентов путем итеративной минимизации ошибки модели на обучающихся данных.

Эта операция называется Градиентный спуск и работает, начиная со случайных значений для каждого коэффициента.

При использовании этого метода необходимо выбрать параметр скорости обучения (альфа), который определяет размер шага улучшения, чтобы взять на себя каждую итерацию процедуры.

На практике градиентный спуск является полезным методом, когда у вас очень большой датасет либо в количестве строк, либо в количестве столбцов, которые могут не уместиться в памяти.

Регуляризация

Есть расширения обучения линейной модели, называемой методами регуляризации. Они направлены как на минимизацию суммы квадратов ошибки модели на обучающих данных (с использованием метода наименьших квадратов), но и на снижения сложности модели (например, количество или абсолютный размер суммы всех коэффициентов в модели).

Два популярных примера процедуры регуляризации линейной регрессии:

Эти методы эффективны в использовании, когда есть коллинерность во входных данных и метод наименьших квадратов соответствует обучающим данным.

Теперь, когда вы знаете некоторые методы изучения коэффициентов в модели линейной регрессии, давайте посмотрим, как мы можем использовать модель для прогнозирования новых данных.

Прогнозирование с помощью с линейной регрессии

Учитывая, что представление является линейным уравнением, сделать прогнозы так же просто, как решение уравнения для определенного набора входов.

Рассмотрим конкретный пример. Представьте, что мы прогнозируем вес человека (y) в зависимости от высоты человека (x). Наше представление модели линейной регрессии для этой проблемы будет:

вес человека = B0 + B1 * высота человека

Например, позволяет использовать B0 = 0,1 и B1 = 0,5. Давайте подставим их и рассчитаем вес (в килограммах) для человека с ростом 182 сантиметра.

вес человека = 0,1 + 0,5 * 182

Вы можете видеть, что вышеупомянутое уравнение может быть отображена как линия в двух измерениях. Коэффициент B0 является нашей отправной точкой независимо от того, какой рост у человека. Мы можем пробежать через различные высоту человека от 100 до 200 сантиметров подставив в уравнению и получить значения веса, создавая нашу линию.

Пример высоты против веса линейной регрессии

Теперь, когда мы знаем, как делать прогнозы с учетом выученной модели линейной регрессии, давайте посмотрим на некоторые правила для подготовки наших данных, чтобы максимально получить от этого типа модели.

Подготовка данных к линейной регрессии

Линейная регрессия изучается уже давно, и есть много литературы о том, как ваши данные должны быть структурированы, чтобы наилучшим образом использовать модель МНК или Градиентного спуска.

Таким образом, когда речь идет об этих требованиях и ожиданиях, они могут быть пугающими. Эти правила можно использовать скорее как практические правила при использовании алгоритмов линейной регрессии.

Используя эти эвристики и посмотреть, что лучше всего работает для вашей проблемы:

Научим основам Python и Data Science на практике

Это не обычный теоритический курс, а онлайн-тренажер, с практикой на примерах рабочих задач, в котором вы можете учиться в любое удобное время 24/7. Вы получите реальный опыт, разрабатывая качественный код и анализируя реальные данные.

Источник