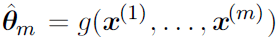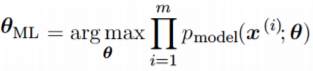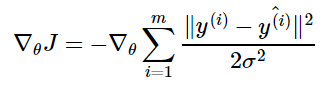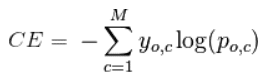функционал ошибки машинное обучение

Понимание 3 наиболее распространенных функций потерь для регрессии машинного обучения

Дата публикации May 20, 2019

Функция потерь в машинном обучении является мерой того, насколько точно ваша модель ML способна предсказать ожидаемый результат, т.е. основную правду.

Функция потерь примет в качестве входных данных два элемента: выходное значение нашей модели и ожидаемое истинное значение. Выход функции потерь называетсяпотерячто является показателем того, насколько хорошо наша модель справилась с прогнозированием результата.

Высокое значение потери означает, что наша модель работает очень плохо. Низкое значение потерь означает, что наша модель работает очень хорошо.

В этой статье мы рассмотрим 3 наиболее распространенных функции потерь для регрессии машинного обучения. Я объясню, как они работают, их плюсы и минусы, и как их можно наиболее эффективно применять при обучении регрессионным моделям.

(1) Средняя квадратическая ошибка (MSE)

Среднеквадратичная ошибка (MSE), возможно, является самой простой и наиболее распространенной функцией потерь, которую часто преподают на вводных курсах машинного обучения. Чтобы рассчитать MSE, вы берете разницу между предсказаниями вашей модели и основополагающей правдой, возводите ее в квадрат и усредняете ее по всему набору данных.

MSE никогда не будет отрицательным, так как мы всегда возводим в квадрат ошибки. MSE формально определяется следующим уравнением:

гдеNколичество образцов, с которыми мы тестируем Код достаточно прост, мы можем написать его в виде простого кода и построить его с помощью matplotlib:

Преимущество:MSE отлично подходит для гарантии того, что наша обученная модель не имеет прогнозируемых выбросов с огромными ошибками, поскольку MSE придает большее значение этим ошибкам из-за квадратной части функции.

Недостаток:Если наша модель делает одно очень плохое предсказание, то квадратичная часть функции увеличивает ошибку. Тем не менее, во многих практических случаях мы не очень заботимся об этих выбросах и стремимся к более всесторонней модели, которая достаточно хороша для большинства.

(2) Средняя абсолютная ошибка (MAE)

Средняя абсолютная ошибка (MAE) лишь немного отличается по определению от MSE, но, что интересно, обеспечивает почти совершенно противоположные свойства! Чтобы рассчитать MAE, вы берете разницу между предсказаниями вашей модели и основополагающей правдой, применяете абсолютное значение к этой разнице и затем усредняете его по всему набору данных.

MAE, как и MSE, никогда не будет отрицательным, так как в этом случае мы всегда принимаем абсолютное значение ошибок. MAE формально определяется следующим уравнением:

Еще раз наш код очень прост в Python! Мы можем написать его в виде простого numpy и построить его с помощью matplotlib. На этот раз мы нарисуем его красным прямо над MSE, чтобы увидеть, как они сравниваются.

Преимущество:Прелесть MAE заключается в том, что его преимущество напрямую покрывает недостаток MSE. Поскольку мы берем абсолютное значение, все ошибки будут взвешены в одной линейной шкале. Таким образом, в отличие от MSE, мы не будем придавать слишком большой вес нашим выбросам, а наша функция потерь обеспечивает общую и даже меру того, насколько хорошо работает наша модель.

Недостаток:Если мы действительно заботимся о прогнозируемых отклонениях нашей модели, то MAE не будет столь же эффективным. Большие ошибки, возникающие из-за выбросов, в конечном итоге взвешиваются точно так же, как и более низкие ошибки. Это может привести к тому, что наша модель в большинстве случаев будет отличной, но время от времени делает несколько очень плохих прогнозов.

(3) Huber Loss

Функция Huber Loss,

Huber Loss предлагает лучшее из обоих миров, уравновешивая MSE и MAE. Мы можем определить его, используя следующую кусочную функцию:

По сути, это уравнение гласит: для значений потерь меньше дельты используйте MSE; для значений потерь больше, чем дельта, используйте MAE Это эффективно объединяет лучшее из обоих миров из двух функций потерь!

Использование MAE для больших значений потерь уменьшает вес, который мы придаем выбросам, так что мы по-прежнему получаем хорошо округленную модель. В то же время мы используем MSE для меньших значений потерь, чтобы поддерживать квадратичную функцию вблизи центра.

Это приводит к увеличению значений потерь до тех пор, пока они превышают 1. Как только потеря для этих точек данных падает ниже 1, квадратичная функция понижает их вес, чтобы сосредоточить обучение на точках данных с более высокой ошибкой.

Проверьте код ниже для функции Huber Loss. Мы также строим график потери Хьюбера рядом с MSE и MAE, чтобы сравнить разницу.

Обратите внимание на то, как мы можем получить потери Хубера прямо между MSE и MAE.

Лучшее обоих миров!

Вы захотите использовать потерю Хубера в любое время, когда почувствуете, что вам необходим баланс между приданием выбросам некоторого веса, но не слишком большого. Для случаев, когда выбросы очень важны для вас, используйте MSE! В тех случаях, когда вы не заботитесь о выбросах, используйте MAE!

Нравится учиться?

Следуй за мной пощебетгде я публикую все о новейших и лучших ИИ, технологиях и науке! Связаться со мной наLinkedInслишком!

Рекомендуемое чтение

И просто напоследок, я поддерживаю этот блог с помощью партнерских ссылок Amazon на замечательные книги, потому что обмен отличными книгами помогает всем! Как партнер Amazon я зарабатываю на соответствующих покупках.

Источник

Русские Блоги

5 функций потери регрессии, обычно используемых в машинном обучении

«Функция потерь» является важной частью оптимизации машинного обучения. Считается, что функции потерь L1 и L2 знакомы большинству людей. Знаете ли вы потерю Губера, потерю Лог-Коша и потерю квантиля, которые обычно используются для расчета интервалов прогнозирования? Это наиболее часто используемые функции потери регрессии для машинного обучения, Даниэль!

Все алгоритмы в машинном обучении должны максимизировать или минимизировать функцию, которая называется «целевой функцией». из их, Обычно мы называем тип минимизированной функции «функцией потерь». Он может измерять способность прогнозирования модели в соответствии с результатом прогнозирования.

В практических применениях выбор функции потерь будет ограничен многими факторами, такими как наличие выбросов, выбор алгоритмов машинного обучения, сложность во времени градиентного спуска, сложность получения производной и достоверность предсказанного значения. Следовательно, не существует одной функции потерь, подходящей для обработки всех типов данных. В этой статье будут представлены различные типы функций потерь и их роль.

Функции потерь можно условно разделить на две категории: Функция потерь задачи классификации и функция потерь задачи регрессии. В этой статье я остановлюсь на потере регрессии.

Мы сохранили коды и диаграммы в этой статье здесь: https://nbviewer.jupyter.org/github/groverpr/Machine-Learning/blob/master/notebooks/05_Loss_Functions.ipynb

Сравнение функций потерь для задач классификации и регрессии

Прогнозируемое значение потерь MSE (ось Y) (ось X)

Среднее абсолютное значение погрешности L1 потерь

Сравнение MSE и MAE

Проще говоря, MSE легко рассчитать, но MAE более устойчив к выбросам. Давайте представим причины различий между ними.

Ниже приведен код Python для этих двух функций потерь. Вы можете написать свои собственные функции или использовать встроенные функции sklearn.

Давайте рассмотрим результаты расчета MAE и RMSE (то есть квадратный корень из MSE с той же величиной, что и MAE) в двух примерах. В первом примере прогнозируемое значение очень близко к истинному значению, и дисперсия ошибки также мала. Во втором примере ошибка очень велика из-за ненормальной точки.

Слева: ошибка относительно близка. Справа: одна ошибка намного больше, чем другие

Что вы можете узнать по картинке? Как выбрать функцию потерь?

MSE возводит в квадрат ошибку (пусть e = значение, предсказанное истинным значением), поэтому, если e> 1, MSE еще больше увеличит ошибку. Если в данных есть аномалия, значение e будет большим, и e² будет намного больше, чем | e |.

Интуитивно это можно понять следующим образом: если мы минимизируем MSE, чтобы дать только одно прогнозируемое значение для всех точек выборки, то это значение должно быть средним из всех целевых значений. Однако, если MAE минимизирован, то это значение будет медианой целевых значений всех точек выборки. Как мы все знаем, для выбросов, Медиана является более устойчивой, чем средняя, ​​поэтому MAE также более устойчив к выбросам, чем MSE.

Однако MAE имеет серьезную проблему (особенно для нейронных сетей): обновленный градиент всегда один и тот же, то есть даже для небольших значений потерь градиент велик. Это не способствует модели обучения. Чтобы устранить этот дефект, мы можем использовать переменную скорость обучения, чтобы уменьшить скорость обучения, когда потери близки к минимуму.

MSE очень хорошо работает в этой ситуации и может эффективно сходиться даже при фиксированной скорости обучения. Градиент потерь MSE увеличивается с увеличением потерь и уменьшается, когда потери приближаются к нулю. Это делает результаты использования модели MSE более точными в конце обучения.

Выберите функцию потерь в соответствии с различными ситуациями

Если ненормальная точка представляет ненормальную ситуацию, которая очень важна в бизнесе и должна быть обнаружена, следует использовать функцию потери MSE. Наоборот, если только поврежденные данные рассматриваются как ненормальные значения, следует использовать функцию потерь MAE.

Проблема обоих заключается в том, что в некоторых случаях две вышеуказанные функции потерь не могут удовлетворить спрос. Например, если 90% выборок в данных соответствуют целевому значению 150, оставшиеся 10% находятся в диапазоне от 0 до 30. Тогда модель, использующая MAE в качестве функции потерь, может игнорировать выброс на 10%, и прогнозируемое значение для всех выборок составляет 150.

Это потому, что модель предсказывает по медиане. Модель, использующая MSE, даст много значений прогнозирования между 0 и 30, потому что модель сместится к ненормальной точке. Приведенные выше два результата нежелательны во многих бизнес-сценариях.

Потеря Хьюбера, сглаженная средняя абсолютная ошибка

Потеря Губера не так чувствительна к выбросам в данных, как потеря квадрата ошибки. Это может также быть дифференцировано в 0. По сути, потеря Хьюбера является абсолютной ошибкой, но она становится квадратной ошибкой, когда ошибка мала. Сколько часов ошибка падает до вторичной ошибки, определяется гиперпараметром дельта (delta). Когда потеря Хьюбера находится между [0-δ, 0 + δ], она эквивалентна MSE, и это MAE, когда [-∞, δ] и [δ, + ∞]

График потерь Хьюбера (ось Y) и прогнозируемого значения (ось X). Истинное значение 0

Выбор гиперпараметра дельта здесь очень важен, потому что он определяет ваше определение аномальных точек. Когда остаток больше дельты, для минимизации следует использовать L1 (менее чувствительный к большим выбросам), а остаток меньше гиперпараметра, тогда для минимизации следует использовать L2.

Источник

Функция потерь (Loss Function)

Функция потерь (Loss Function, Cost Function, Error Function; J) – фрагмент программного кода, который используется для оптимизации Алгоритма (Algorithm) Машинного обучения (ML). Значение, вычисленное такой функцией, называется «потерей».

Функция (Function) потерь может дать бо́льшую практическую гибкость вашим Нейронным сетям (Neural Network) и будет определять, как именно выходные данные связаны с исходными.

Нейронные сети могут выполнять несколько задач: от прогнозирования непрерывных значений, таких как ежемесячные расходы, до Бинарной классификации (Binary Classification) на кошек и собак. Для каждой отдельной задачи потребуются разные типы функций, поскольку выходной формат индивидуален.

С очень упрощенной точки зрения Loss Function может быть определена как функция, которая принимает два параметра:

Эта функция, по сути, вычислит, насколько хорошо работает наша модель, сравнив то, что модель прогнозирует, с фактическим значением, которое она должна выдает. Если Y_pred очень далеко от Yi, значение потерь будет очень высоким. Однако, если оба значения почти одинаковы, значение потерь будет очень низким. Следовательно, нам нужно сохранить функцию потерь, которая может эффективно наказывать модель, пока та обучается на Тренировочных данных (Train Data).

Этот сценарий в чем-то аналогичен подготовке к экзаменам. Если кто-то плохо сдает экзамен, мы можем сказать, что потеря очень высока, и этому человеку придется многое изменить внутри себя, чтобы в следующий раз получить лучшую оценку. Однако, если экзамен пройдет хорошо, студент может вести себя подобным образом и в следующий раз.

Теперь давайте рассмотрим классификацию как задачу и поймем, как в этом случае работает функция потерь.

Классификационные потери

Когда нейронная сеть пытается предсказать дискретное значение, мы рассматриваем это как модель классификации. Это может быть сеть, пытающаяся предсказать, какое животное присутствует на изображении, или является ли электронное письмо спамом. Сначала давайте посмотрим, как представлены выходные данные классификационной нейронной сети.

Выходной формат данных нейросети бинарной классификации

Количество узлов выходного слоя будет зависеть от количества классов, присутствующих в данных. Каждый узел будет представлять один класс. Значение каждого выходного узла по существу представляет вероятность того, что этот класс является правильным.

Как только мы получим вероятности всех различных классов, рассмотрим тот, что имеет наибольшую вероятность. Посмотрим, как выполняется двоичная классификация.

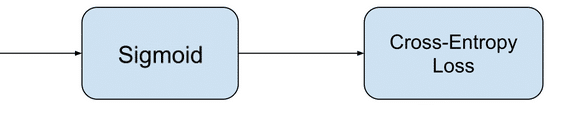
Бинарная классификация

В двоичной классификации на выходном слое будет только один узел. Чтобы получить результат в формате вероятности, нам нужно применить Функцию активации (Activation Function). Поскольку для вероятности требуется значение от 0 до 1, мы будем использовать Сигмоид (Sigmoid), которая приведет любое реальное значение к диапазону значений от 0 до 1.

Визуализация преобразования значения сигмоидом

По мере того, как входные реальные данные становятся больше и стремятся к плюс бесконечности, выходные данные сигмоида будут стремиться к единице. А когда на входе значения становятся меньше и стремятся к отрицательной бесконечности, на выходе числа будут стремиться к нулю. Теперь мы гарантированно получаем значение от 0 до 1, и это именно то, что нам нужно, поскольку нам нужны вероятности.

Если выход выше 0,5 (вероятность 50%), мы будем считать, что он попадает в положительный класс, а если он ниже 0,5, мы будем считать, что он попадает в отрицательный класс. Например, если мы обучаем нейросеть для классификации кошек и собак, мы можем назначить собакам положительный класс, и выходное значение в наборе данных для собак будет равно 1, аналогично кошкам будет назначен отрицательный класс, а выходное значение для кошек будет быть 0.

Функция потерь, которую мы используем для двоичной классификации, называется Двоичной перекрестной энтропией (BCE). Эта функция эффективно наказывает нейронную сеть за Ошибки (Error) двоичной классификации. Давайте посмотрим, как она выглядит.

Графики потери бинарной кросс-энтропии

Как видите, есть две отдельные функции, по одной для каждого значения Y. Когда нам нужно предсказать положительный класс (Y = 1), мы будем использовать следующую формулу:

И когда нам нужно предсказать отрицательный класс (Y = 0), мы будем использовать немного трансформированный аналог:

Для первой функции, когда Y_pred равно 1, потеря равна 0, что имеет смысл, потому что Y_pred точно такое же, как Y. Когда значение Y_pred становится ближе к 0, мы можем наблюдать, как значение потери сильно увеличивается. Когда же Y_pred становится равным 0, потеря стремится к бесконечности. Это происходит, потому что с точки зрения классификации, 0 и 1 – полярные противоположности: каждый из них представляет совершенно разные классы. Поэтому, когда Y_pred равно 0, а Y равно 1, потери должны быть очень высокими, чтобы сеть могла более эффективно распознавать свои ошибки.

Сравнение потерь двоичной классификации

Полиномиальная классификация

Полиномиальная классификация (Multiclass Classification) подходит, когда нам нужно, чтобы наша модель каждый раз предсказывала один возможный класс. Теперь, поскольку мы все еще имеем дело с вероятностями, имеет смысл просто применить сигмоид ко всем выходным узлам, чтобы мы получали значения от 0 до 1 для всех выходных значений, но здесь кроется проблема. Когда мы рассматриваем вероятности для нескольких классов, нам необходимо убедиться, что сумма всех индивидуальных вероятностей равна единице, поскольку именно так определяется вероятность. Применение сигмоида не гарантирует, что сумма всегда равна единице, поэтому нам нужно использовать другую функцию активации.

В данном случае мы используем функцию активации Softmax. Эта функция гарантирует, что все выходные узлы имеют значения от 0 до 1, а сумма всех значений выходных узлов всегда равна 1. Вычисляется с помощью формулы:

Как видите, мы просто передаем все значения в экспоненциальную функцию. После этого, чтобы убедиться, что все они находятся в диапазоне от 0 до 1 и сумма всех выходных значений равна 1, мы просто делим каждую экспоненту на сумму экспонент.

Итак, почему мы должны передавать каждое значение через экспоненту перед их нормализацией? Почему мы не можем просто нормализовать сами значения? Это связано с тем, что цель Softmax – убедиться, что одно значение очень высокое (близко к 1), а все остальные значения очень низкие (близко к 0). Softmax использует экспоненту, чтобы убедиться, что это произойдет. А затем мы нормализуем результат, потому что нам нужны вероятности.

Теперь, когда наши выходные данные имеют правильный формат, давайте посмотрим, как мы настраиваем для этого функцию потерь. Хорошо то, что функция потерь по сути такая же, как у двоичной классификации. Мы просто применим Логарифмическую потерю (Log Loss) к каждому выходному узлу по отношению к его соответствующему целевому значению, а затем найдем сумму этих значений по всем выходным узлам.

Категориальная кросс-энтропия

Эта потеря называется категориальной Кросс-энтропией (Cross Entropy). Теперь перейдем к частному случаю классификации, называемому многозначной классификацией.

Классификация по нескольким меткам

Классификация по нескольким меткам (MLC) выполняется, когда нашей модели необходимо предсказать несколько классов в качестве выходных данных. Например, мы тренируем нейронную сеть, чтобы предсказывать ингредиенты, присутствующие на изображении какой-то еды. Нам нужно будет предсказать несколько ингредиентов, поэтому в Y будет несколько единиц.

Для этого мы не можем использовать Softmax, потому что он всегда заставляет только один класс «становиться единицей», а другие классы приводит к нулю. Вместо этого мы можем просто сохранить сигмоид на всех значениях выходных узлов, поскольку пытаемся предсказать индивидуальную вероятность каждого класса.

Что касается потерь, мы можем напрямую использовать логарифмические потери на каждом узле и суммировать их, аналогично тому, что мы делали в мультиклассовой классификации.

Теперь, когда мы рассмотрели классификацию, перейдем к регрессии.

Потеря регрессии

В Регрессии (Regression) наша модель пытается предсказать непрерывное значение, например, цены на жилье или возраст человека. Наша нейронная сеть будет иметь один выходной узел для каждого непрерывного значения, которое мы пытаемся предсказать. Потери регрессии рассчитываются путем прямого сравнения выходного и истинного значения.

Самая популярная функция потерь, которую мы используем для регрессионных моделей, – это Среднеквадратическая ошибка (MSE). Здесь мы просто вычисляем квадрат разницы между Y и Y_Pred и усредняем полученное значение.

Источник

Функции оценки, потерь, оптимизации – основы алгоритма Машинного Обучения

Адаптированный перевод прекрасной статьи энтузиаста технологий машинного обучения Javaid Nabi.

Чтобы понимать как алгоритм машинного обучения учится предсказывать результаты на основе данных, важно разобраться в основных концепциях и понятиях, используемых при обучении алгоритма.

Функции оценки

В контексте технологии машинного обучения, оценка – это статистический термин для нахождения некоторого приближения неизвестного параметра на основе некоторых данных. Точечная оценка – это попытка найти единственное лучшее приближение некоторого количества интересующих нас параметров. Или на более формальном языке математической статистики — точечная оценка это число, оцениваемое на основе наблюдений, предположительно близкое к оцениваемому параметру.

Под количеством интересующих параметров обычно подразумевается:
• Один параметр
• Вектор параметров – например, веса в линейной регрессии
• Целая функция

Точечная оценка

Такое определение точечной оценки является очень общим и предоставляет разработчику большую свободу действий. Почти любая функция, таким образом, может рассматриваться как оценщик, но хороший оценщик – это функция, значения которой близки к истинному базовому значению θ, которое сгенерированно обучающими данными.

Точечная оценка также может относиться к оценке взаимосвязи между входными и целевыми переменными, в этом случае чаще называемой функцией оценки.

Функция оценки

Задача, решаемая машинным обучением, заключается в попытке предсказать переменную y по заданному входному вектору x. Мы предполагаем, что существует функция f(x), которая описывает приблизительную связь между y и x. Например, можно предположить, что y = f(x) + ε, где ε обозначает часть y, которая явно не предсказывается входным вектором x. При оценке функций нас интересует приближение f с помощью модели или оценки fˆ. Функция оценки в действительности это тоже самое, что оценка параметра θ; функция оценки f это просто точечная оценка в функциональном пространстве. Пример: в полиномиальной регрессии мы либо оцениваем параметр w, либо оцениваем функцию отображения из x в y.

Смещение и дисперсия

Смещение и дисперсия измеряют два разных источника ошибки функции оценки. Смещение измеряет ожидаемое отклонение от истинного значения функции или параметра. Дисперсия, с другой стороны, показывает меру отклонения от ожидаемого значения оценки, которую может вызвать любая конкретная выборка данных.

Смещение

Смещение определяется следующим образом:

где ожидаемое значение E(θˆ_m) для данных (рассматриваемых как выборки из случайной величины) и θ является истинным базовым значением, используемым для определения распределения, генерирующего данные.

Оценщик θˆ_m называется несмещенным, если bias(θˆ_m)=0, что подразумевает что E(θˆ_m) = θ.

Дисперсия и Стандартная ошибка

Дисперсия оценки обозначается как Var(θˆ), где случайная величина является обучающим множеством. Альтернативно, квадратный корень дисперсии называется стандартной ошибкой, обозначаемой как SE(θˆ). Дисперсия или стандартная ошибка оценщика показывает меру ожидания того, как оценка, которую мы вычисляем, будет изменяться по мере того, как мы меняем выборки из базового набора данных, генерирующих процесс.

Точно так же, как мы хотели бы, чтобы функция оценки имела малое смещение, мы также стремимся, чтобы у нее была относительно низкая дисперсия.

Давайте теперь рассмотрим некоторые обычно используемые функции оценки.

Оценка Максимального Правдоподобия (MLE)

Оценка максимального правдоподобия может быть определена как метод оценки параметров (таких как среднее значение или дисперсия) из выборки данных, так что вероятность получения наблюдаемых данных максимальна.

Оценка максимального правдоподобия для θ определяется как:

Поскольку мы предположили, что примеры являются независимыми выборками, приведенное выше уравнение можно записать в виде:

Эта произведение многих вероятностей может быть неудобным по ряду причин. В частности, оно склонно к числовой недооценке. Кроме того, чтобы найти максимумы/минимумы этой функции, мы должны взять производную этой функции от θ и приравнять ее к 0. Поскольку это произведение членов, нам нужно применить правило цепочки, которое довольно громоздко. Чтобы получить более удобную, но эквивалентную задачу оптимизации, можно использовать логарифм вероятности, который не меняет его argmax, но удобно превращает произведение в сумму, и поскольку логарифм – строго возрастающая функция (функция натурального логарифма – монотонное преобразование), это не повлияет на итоговое значение θ.

Два важных свойства: сходимость и эффективность

Сходимость. По мере того, как число обучающих выборок приближается к бесконечности, оценка максимального правдоподобия сходится к истинному значению параметра.

Эффективность. Способ измерения того, насколько мы близки к истинному параметру, – это ожидаемая средняя квадратичная ошибка, вычисление квадратичной разницы между оценочными и истинными значениями параметров, где математическое ожидание вычисляется над m обучающими выборками из данных, генерирующих распределение. Эта параметрическая среднеквадратичная ошибка уменьшается с увеличением m, и для больших m нижняя граница неравенства Крамера-Рао показывает, что ни у одной сходящейся функции оценки нет среднеквадратичной ошибки меньше, чем у оценки максимального правдоподобия.

Именно по причине сходимости и эффективности, оценка максимального правдоподобия часто считается предпочтительным оценщиком для машинного обучения.

Когда количество примеров достаточно мало, чтобы привести к переобучению, стратегии регуляризации, такие как понижающие веса, могут использоваться для получения смещенной версии оценки максимального правдоподобия, которая имеет меньшую дисперсию, когда данные обучения ограничены.

Максимальная апостериорная (MAP) оценка

Согласно байесовскому подходу, можно учесть влияние предварительных данных на выбор точечной оценки. MAP может использоваться для получения точечной оценки ненаблюдаемой величины на основе эмпирических данных. Оценка MAP выбирает точку максимальной апостериорной вероятности (или максимальной плотности вероятности в более распространенном случае непрерывного θ):

где с правой стороны, log(p(x|θ)) – стандартный член логарифмической вероятности и log(p(θ)) соответствует изначальному распределению.

Как и при полном байесовском методе, байесовский MAP имеет преимущество
использования изначальной информации, которой нет в обучающих данных. Эта дополнительная информация помогает уменьшить дисперсию для точечной оценки MAP (по сравнению с оценкой MLE). Однако, это происходит ценой повышенного смещения.

Функции потерь

В большинстве обучающих сетей ошибка рассчитывается как разница между фактическим выходным значением y и прогнозируемым выходным значением ŷ. Функция, используемая для вычисления этой ошибки, известна как функция потерь, также часто называемая функцией ошибки или затрат.

До сих пор наше основное внимание уделялось оценке параметров с помощью MLE или MAP. Причина, по которой мы обсуждали это раньше, заключается в том, что и MLE, и MAP предоставляют механизм для получения функции потерь.

Давайте рассмотрим некоторые часто используемые функции потерь.

Средняя квадратичная ошибка (MSE): средняя квадратичная ошибка является наиболее распространенной функцией потерь. Функция потерь MSE широко используется в линейной регрессии в качестве показателя эффективности. Чтобы рассчитать MSE, надо взять разницу между предсказанными значениями и истинными, возвести ее в квадрат и усреднить по всему набору данных.

где y (i) – фактический ожидаемый результат, а ŷ (i) – прогноз модели.

Многие функции потерь (затрат), используемые в машинном обучении, включая MSE, могут быть получены из метода максимального правдоподобия.

Чтобы увидеть, как мы можем вывести функции потерь из MLE или MAP, требуется некоторая математика. Вы можете пропустить ее и перейти к следующему разделу.

Получение MSE из MLE

Можно смоделировать модель линейной регрессии следующим образом:

мы предполагаем, что у имеет нормальное распределение с ŷ в качестве среднего значения распределения и некоторой постоянной σ² в качестве дисперсии, выбранной пользователем. Нормальное распределения являются разумным выбором во многих случаях. В отсутствие предварительных данных о том, какое распределение в действительности соответствует рассматриваемым данным, нормальное распределение является хорошим выбором по умолчанию.

Вернемся к логарифмической вероятности, определенной ранее:

где ŷ(i) – результат линейной регрессии на i-м входе, а m – количество обучающих примеров. Мы видим, что две первые величины являются постоянными, поэтому максимизация логарифмической вероятности сводится к минимизации MSE:

Таким образом, максимизация логарифмического правдоподобия относительно θ дает такую же оценку параметров θ, что и минимизация среднеквадратичной ошибки. Два критерия имеют разные значения, но одинаковое расположение оптимума. Это оправдывает использование MSE в качестве функции оценки максимального правдоподобия.

Кросс-энтропия (или логарифмическая функция потерь – log loss): Кросс-энтропия измеряет расхождение между двумя вероятностными распределениями. Если кросс-энтропия велика, это означает, что разница между двумя распределениями велика, а если кросс-энтропия мала, то распределения похожи друг на друга.

Кросс-энтропия определяется как:

где P – распределение истинных ответов, а Q – распределение вероятностей прогнозов модели. Можно показать, что функция кросс-энтропии также получается из MLE, но я не буду утомлять вас большим количеством математики.

Давайте еще упростим это для нашей модели с:
• N – количество наблюдений
• M – количество возможных меток класса (собака, кошка, рыба)
• y – двоичный индикатор (0 или 1) того, является ли метка класса C правильной классификацией для наблюдения O
• p – прогнозируемая вероятность модели

Бинарная классификация

В случае бинарной классификации (M=2), формула имеет вид:

При двоичной классификации каждая предсказанная вероятность сравнивается с фактическим значением класса (0 или 1), и вычисляется оценка, которая штрафует вероятность на основе расстояния от ожидаемого значения.

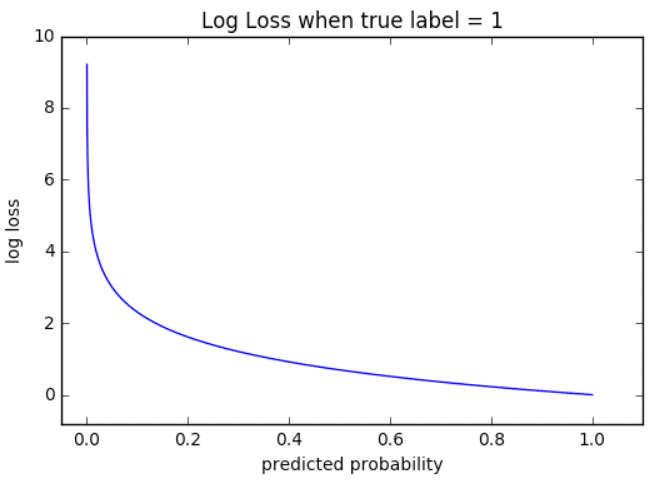
Визуализация

На приведенном ниже графике показан диапазон возможных значений логистической функции потерь с учетом истинного наблюдения (y = 1). Когда прогнозируемая вероятность приближается к 1, логистическая функция потерь медленно уменьшается. Однако при уменьшении прогнозируемой вероятности она быстро возрастает.

Логистическая функция потерь наказывает оба типа ошибок, но особенно те прогнозы, которые являются достоверными и ошибочными!

Мульти-классовая классификация

В случае мульти-классовой классификации (M>2) мы берем сумму значений логарифмических функций потерь для каждого прогноза наблюдаемых классов.

Кросс-энтропия для бинарной или двух-классовой задачи прогнозирования фактически рассчитывается как средняя кросс-энтропия среди всех примеров. Log loss использует отрицательные значения логарифма, чтобы обеспечить удобную метрику для сравнения. Этот подход основан на том, что логарифм чисел

Задача бинарной классификации

Задача состоит в том, чтобы классифицировать пример как принадлежащий одному из двух классов. Или более точно, задача сформулирована как предсказание вероятности того, что пример принадлежит первому классу, например, классу, которому вы присваиваете целочисленное значение 1, тогда как другому классу присваивается значение 0.

• Конфигурация выходного уровня: один узел с сигмовидной активационной функцией.
• Функция потерь: кросс-энтропия, также называемая логарифмической функцией потерь.

Задача мульти-классовой классификации

Эта задача состоит в том, чтобы классифицировать пример как принадлежащий одному из нескольких классов. Задача сформулирована как предсказание вероятности того, что пример принадлежит каждому классу.

• Конфигурация выходного уровня: один узел для каждого класса, использующий функцию активации softmax.
• Функция потерь: кросс-энтропия, также называемая логарифмической функцией потерь.

Рассмотрев оценку и различные функции потерь, давайте перейдем к роли оптимизаторов в алгоритмах ML.

Оптимизаторы

Чтобы свести к минимуму ошибку или потерю в прогнозировании, модель, используя примеры из обучающей выборки, обновляет параметры модели W. Расчеты ошибок строятся в зависимости от W и также описываются графиком функции затрат J(w), поскольку она определяет затраты/наказание модели. Таким образом, минимизация ошибки также часто называется минимизацией функции затрат.

Но как именно это делается? Используя оптимизаторы.

Оптимизаторы используются для обновления весов и смещений, то есть внутренних параметров модели, чтобы уменьшить ошибку.

Самым важным методом и основой того, как мы обучаем и оптимизируем нашу модель, является метод Градиентного Спуска.

Градиентный Спуск

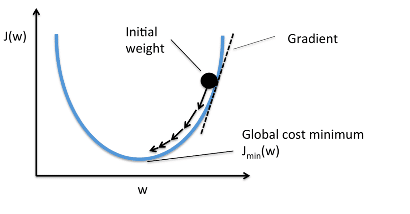
Когда мы строим функцию затрат J(w), это можно представить следующим образом:

Как видно из кривой, существует значение параметров W, которое имеет минимальное значение J_min. Нам нужно найти способ достичь этого минимального значения.

В алгоритме градиентного спуска мы начинаем со случайных параметров модели и вычисляем ошибку для каждой итерации обучения, продолжая обновлять параметры, чтобы приблизиться к минимальным значениям.

Повторяем до достижения минимума:

В приведенном выше уравнении мы обновляем параметры модели после каждой итерации. Второй член уравнения вычисляет наклон или градиент кривой на каждой итерации.

Градиент функции затрат вычисляется как частная производная функции затрат J по каждому параметру модели W_j, где j принимает значение числа признаков [1, n]. α – альфа, это скорость обучения, определяющий как быстро мы хотим двигаться к минимуму. Если α слишком велико, мы можем проскочить минимум. Если α слишком мало, это приведет к небольшим этапам обучения, поэтому общее время, затрачиваемое моделью для достижения минимума, будет больше.

Есть три способа сделать градиентный спуск:

Пакетный градиентный спуск: использует все обучающие данные для обновления параметров модели в каждой итерации.

Мини-пакетный градиентный спуск: вместо использования всех данных, мини-пакетный градиентный спуск делит тренировочный набор на меньший размер, называемый партией, и обозначаемый буквой «b». Таким образом, мини-пакет «b» используется для обновления параметров модели на каждой итерации.

Вот некоторые другие часто используемые Оптимизаторы:

Стохастический Градиентный Спуск (SGD): обновляет параметры, используя только один обучающий параметр на каждой итерации. Такой параметр обычно выбирается случайным образом. Стохастический градиентный спуск часто предпочтителен для оптимизации функций затрат, когда есть сотни тысяч обучающих или более параметров, поскольку он будет сходиться быстрее, чем пакетный градиентный спуск.

Адаград

Адаград адаптирует скорость обучения конкретно к индивидуальным особенностям: это означает, что некоторые веса в вашем наборе данных будут отличаться от других. Это работает очень хорошо для разреженных наборов данных, где пропущено много входных значений. Однако, у Адаграда есть одна серьезная проблема: адаптивная скорость обучения со временем становится очень маленькой.

Некоторые другие оптимизаторы, описанные ниже, пытаются справиться с этой проблемой.

RMSprop

RMSprop – это специальная версия Adagrad, разработанная профессором Джеффри Хинтоном в его классе нейронных сетей. Вместо того, чтобы вычислять все градиенты, он вычисляет градиенты только в фиксированном окне. RMSprop похож на Adaprop, это еще один оптимизатор, который пытается решить некоторые проблемы, которые Адаград оставляет открытыми.

Адам означает адаптивную оценку момента и является еще одним способом использования предыдущих градиентов для вычисления текущих градиентов. Адам также использует концепцию импульса, добавляя доли предыдущих градиентов к текущему. Этот оптимизатор получил довольно широкое распространение и практически принят для использования в обучающих нейронных сетях.

Вы только что ознакомились с кратким обзором оптимизаторов. Более подробно об этом можно прочитать здесь.

Я надеюсь, что после прочтения этой статьи, вы будете лучше понимать что происходит, когда Вы пишите следующий код:

Спасибо за проявленный интерес!

Источник