главный смысл обучения с подкреплением это
Обучение с подкреплением на нейронных сетях. Теория
Так мне указали, что для задачи классификации — нейронные сети (обучение с учителем), генетические алгоритмы (обучение без учителя) — задача кластеризации, а еще есть обучение с подкреплением (Q-обучение) — как задача агента, который бродит и что-то делает. И вот такими шаблонами многие и судят.
Попробуем разобраться, что дает применение нейронных сетей, как некоторые заявляют, к задаче которую они не могут решить — а именно к обучению с подкреплением.
И заодно проанализируем диссертацию Бурцев М.С., «Исследование новых типов самоорганизации и возникновения поведенческих стратегий», в которой не больше не меньше красиво сделано именно применение простеньких нейронных сетей в задаче обучения с подкреплением.
Теория
В генетических алгоритмах и в методах для обучения с подкреплением (напр., Q-обучение) есть одна существенная проблема — нужно задавать функцию пригодности. Причем она задается явно формулой. Иногда она появляется косвенно — тогда кажется, что этой функции явно нет (это мы проследим далее, на анализе диссертации Бурцева М.С.). И все «чудеса» агентного поведения происходят только от этой формулы.
Но что такое формула? — Функция. Или что тоже самое отображение входов на выходы. А что делает нейронная сеть/перцептрон? Именно это он и делает — обучается отображать входы на выходы.
Возьмем утрированный теоретический пример. Агент — это какой-то организм, которому хочется выжить. Для этого ему надо есть. Он есть два вида животных — ну пусть зайцев и мышей. Соответственно у него есть два входных параметра — количество килограмм, которые содержит съеденная зайчатина и мышатина :). Он (организм) хочет оценивать на сколько он сыт. Тогда в зависимости от того, на сколько он сыт он может бегать с большей или меньшей скоростью и желанием. Но это уже другая задача, а мы остановимся на оценке сытости.
Нам ничего не известно как оценивать сытость, кроме килограмм того и другого. Поэтому первая естественная оценка — это научиться складывать килограммы. Т.е. мы вводим простую функцию пригодности c= a+b. Замечательно, но имея такую жесткую функцию оценки мы не можем корректировать свое поведение.
Поэтому применяется нейронная сеть. Её вначале обучают складывать эти два числа. После обучения нейронная сеть умеет безошибочно складывать. Агент использует выход нейронной сети и понимает на сколько он сыт.
Но далее происходит несчастье — он оценил, что он сыт на 7 баллов = съев 4 кило зайчатины и 3 мышатины. И бегал думая, что наелся, так что чуть не переусердствовал и не помер. Оказалось, что 4 кило зайчатины и 3 мышатины — это не тоже самое, что 7 кило зайчатины. Мышатина не дает такой же сытости, и складывать на самом деле нужно как 4 + 3 = 6. Вот этот сделанный им вывод он и вкидывает как точную данность в нейронную сеть. Она переобучается, и её функция пригодности уже не простое сложение, и приобретает совершенно другой вид. Таким образом, имея нейронную сеть мы может корректировать функцию пригодности, чего не можем делать в других алгоритмах.
Вы можете сказать, что в других алгоритмах надо было просто брать не функцию сложения. Но какую? У вас нет ни соответствующих параметров, ни принципов на которых вы бы вывели нужную закономерность. Вы просто не смогли бы формализовать такую задачу, т.к. не смогли бы понять пространство состояний.
Практика на примере диссертации Бурцева М.С.
Какая у него модельная среда:
Популяция P агентов A, находящихся в одномерной клеточной среде, замкнутой в виде кольца. В клетках с некоторой вероятностью появляется ресурс, необходимый агентам для совершения действий. В одной клетке может находиться только один агент. Агент-потомок может появиться только в результате скрещивания двух агентов-родителей. У агента 9 входов
1,2,3 — 1 если в данной клетке поля зрения (слева, рядом, справа) есть ресурс, 0 в противном случае;
4, 5 — 1 если в клетке слева/справа есть агент, 0 в противном случае;
6,7 — мотивация к скрещиванию Mr соседа слева/справа;
8 — собственная мотивация к поиску пищи
9 — собственная мотивация к скрещиванию
Мотивация к скрещиванию и поиску пищи определяется через отношение двух коэффициентов выбранных экспериментатором — r0 — значения внутреннего ресурса для насыщения и r1 — для скрещивания.
Существует 6 действий: скрещиваться с соседом справа, скрещиваться с соседом слева, прыгать, двигаться на одну клетку вправо, двигаться на одну клетку влево, потреблять ресурс, отдыхать
Была изначально настроенная ИНС, конечно её сетью назвать сложно — без внутреннего слоя, но пусть. Она имела различные коэффициенты, как входы связанны с действиями (выходами). Далее применялся генетический алгоритм, который настраивал коэффициенты нейронной сети, и отбраковал организм с плохим поведением.
По сути генетические алгоритмы тут не сильно и нужны. Можно аналогично случайно перебирать разные стратегии поведения и фиксировать пригодные, корректируя нейронную сеть.
На самом деле, проблема с Q-learning и генетическими алгоритмами заключается в том, что новое поведение ищется случайно. А случайность это равновероятный поиск на всем пространстве возможных состояний. Т.е. в этом нет целенаправленного поиска. А если пространство возможных состояний велико, то элементарные стратегии так никогда и не будут найдены.
Поэтому вообще-то нужно не случайно перебирать разные стратегии, а целенаправленно (но об этом нужно уже говорить в следующей статье после понимания первых штрихов :)).
Я пробежался быстро, т.к. нам важны лишь выводы, а не детали. Но Вам возможно нужно почитать об этом самим подробнее.
В итоге функция пригодности агента представлена нейронной сетью. Как в изложенной теории выше, так и у Бурцева в диссертации.
Но отличаем её от функции пригодности среды. Она тут косвенно задана через коэффициенты r0 и r1. Причем эта функция пригодности среды — экспериментатору известна. Поэтому нет ни какой фантастики, когда Бурцев обнаруживает как функция пригодности агента начинает приближаться к функции пригодности среды.
В статье Проблема «двух и более учителей». Первые штрихи у нас ситуация — хуже. Функцию пригодности среды не знает даже экспериментатор, точнее вид этой функции. В этом то и проблема, она ни как косвенно не определяется. Да, известно лишь конечная функция пригодности — максимум денег, но внутри себя она содержит подфункцию, которая не известна. Функции пригодности агента, надо стремится к этой подфункции — а она не может быть вычислена.
Надеюсь теперь будет немного более понятно.
Введение в обучение с подкреплением: от многорукого бандита до полноценного RL агента
Привет, Хабр! Обучение с подкреплением является одним из самых перспективных направлений машинного обучения. С его помощью искусственный интеллект сегодня способен решать широчайший спектр задач: от робототехники и видеоигр до моделирования поведения покупателей и здравоохранения. В этой вводной статье мы изучим главную идею reinforcement learning и с нуля построим собственного самообучающегося бота.
Введение
Основное отличие обучения с подкреплением (reinforcement learning) от классического машинного обучения заключается в том, что искусственный интеллект обучается в процессе взаимодействия с окружающей средой, а не на исторических данных. Соединив в себе способность нейронных сетей восстанавливать сложные взаимосвязи и самообучаемость агента (системы) в reinforcement learning, машины достигли огромных успехов, победив сначала в нескольких видеоиграх Atari, а потом и чемпиона мира по игре в го.
Если вы привыкли работать с задачами обучения с учителем, то в случае reinforcement learning действует немного иная логика. Вместо того, чтобы создавать алгоритм, который обучается на наборе пар «факторы — правильный ответ», в обучении с подкреплением необходимо научить агента взаимодействовать с окружающей средой, самостоятельно генерируя эти пары. Затем на них же он будет обучаться через систему наблюдений (observations), выигрышей (reward) и действий (actions).
Очевидно, что теперь в каждый момент времени у нас нет постоянного правильного ответа, поэтому задача становится немного хитрее. В этой серии статей мы будем создавать и обучать агентов обучения с подкреплением. Начнем с самого простого варианта агента, чтобы основная идея reinforcement learning была предельно понятна, а затем перейдем к более сложным задачам.
Многорукий бандит
Самый простой пример задачи обучения с подкреплением — задача о многоруком бандите (она достаточно широко освещена на Хабре, в частности, тут и тут). В нашей постановке задачи есть n игровых автоматов, в каждом из которых фиксирована вероятность выигрыша. Тогда цель агента — найти слот-машину с наибольшим ожидаемым выигрышем и всегда выбирать именно ее. Для простоты у нас будет всего четыре игровых автомата, из которых нужно будет выбирать.
По правде говоря, эту задачу можно с натяжкой отнести к reinforcement learning, поскольку задачам из этого класса характерны следующие свойства:
В области обучения с подкреплением есть и другой подход, при котором агенты обучают value functions. Вместо того, чтобы находить оптимальное действие в текущем состоянии, агент учиться предсказывать, насколько выгодно находиться в данном состоянии и совершать данное действие. Оба подхода дают хорошие результаты, однако логика policy gradient более очевидна.
Policy Gradient
Как мы уже выяснили, в нашем случае ожидаемый выигрыш каждого из игровых автоматов не зависит от текущего состояния среды. Получается, что наша нейросеть будет состоять лишь из набора весов, каждый из которых соответствует одному игровому автомату. Эти веса и будут определять, за какую ручку нужно дернуть, чтобы получить максимальный выигрыш. К примеру, если все веса инициализировать равными 1, то агент будет одинаково оптимистичен по поводу выигрыша во всех игровых автоматах.
Для обновления весов модели мы будем использовать e-жадную линию поведения. Это значит, что в большинстве случаев агент будет выбирать действие, максимизирующее ожидаемый выигрыш, однако иногда (с вероятностью равной e) действие будет случайным. Так будет обеспечен выбор всех возможных вариантов, что позволит нейросети «узнать» больше о каждом из них.
Интуитивно понятно, что функция потерь должна принимать такие значения, чтобы веса действий, которые привели к выигрышу увеличивались, а те, которые привели к проигрышу, уменьшались. В результате веса будут обновляться, а агент будет все чаще и чаще выбирать игровой автомат с наибольшей фиксированной вероятностью выигрыша, пока, наконец, он не будет выбирать его всегда.
Реализация алгоритма
Бандиты. Сначала мы создадим наших бандитов (в быту игровой автомат называют бандитом). В нашем примере их будет 4. Функция pullBandit генерирует случайное число из стандартного нормального распределения, а затем сравнивает его со значением бандита и возвращает результат игры. Чем дальше по списку находится бандит, тем больше вероятность, что агент выиграет, выбрав именно его. Таким образом, мы хотим, чтобы наш агент научился всегда выбирать последнего бандита.
Агент. Кусок кода ниже создает нашего простого агента, который состоит из набора значений для бандитов. Каждое значение соответствует выигрышу/проигрышу в зависимости от выбора того или иного бандита. Чтобы обновлять веса агента мы используем policy gradient, то есть выбираем действия, минимизирующие функцию потерь:
Обучение агента. Мы будем обучать агента, путем выбора определенных действий и получения выигрышей/проигрышей. Используя полученные значения, мы будем знать, как именно обновить веса модели, чтобы чаще выбирать бандитов с большим ожидаемым выигрышем:
Полный Jupyter Notebook можно скачать тут.
Решение полноценной задачи обучения с подкреплением
Теперь, когда мы знаем, как создать агента, способного выбирать оптимальное решение из нескольких возможных, перейдем к рассмотрению более сложной задачи, которая и будет представлять собой пример полноценного reinforcement learning: оценивая текущее состояние системы, агент должен выбирать действия, которые максимизируют выигрыш не только сейчас, но и в будущем.
Системы, в которых может быть решена обучения с подкреплением называются Марковскими процессами принятия решений (Markov Decision Processes, MDP). Для таких систем характерны выигрыши и действия, обеспечивающие переход из одного состояния в другое, причем эти выигрыши зависят от текущего состояния системы и решения, которое принимает агент в этом состоянии. Выигрыш может быть получен с задержкой во времени.
Формально Марковский процесс принятия решений может быть определен следующим образом. MDP состоит из набора всех возможных состояний S и действий А, причем в каждый момент времени он находится в состоянии s и совершает действие a из этих наборов. Таким образом, дан кортеж (s, a) и для него определены T(s,a) — вероятность перехода в новое состояние s’ и R(s,a) — выигрыш. В итоге в любой момент времени в MDP агент находится в состоянии s, принимает решение a и в ответ получает новое состояние s’ и выигрыш r.
Для примера, даже процесс открывания двери можно представить в виде Марковского процесса принятия решений. Состоянием будет наш взгляд на дверь, а также расположение нашего тела и двери в мире. Все возможные движения тела, что мы можем сделать, и являются набором A, а выигрыш — это успешное открытие двери. Определенные действия (например, шаг в сторону двери) приближают нас к достижению цели, однако сами по себе не приносят выигрыша, так как его обеспечивает только непосредственно открывание двери. В итоге, агент должен совершать такие действия, которые рано или поздно приведут к решению задачи.
Задача стабилизации перевернутого маятника
Воспользуемся OpenAI Gym — платформой для разработки и тренировки AI ботов с помощью игр и алгоритмических испытаний и возьмем классическую задачу оттуда: задача стабилизации перевернутого маятника или Cart-Pole. В нашем случае суть задачи заключается в том, чтобы как можно дольше удерживать стержень в вертикальном положении, двигая тележку по горизонтали:
В отличии от задачи о многоруком бандите, в данной системе есть:
Таким образом, каждое действие агента будет совершено с учетом не только мгновенного выигрыша, но и всех последующих. Также теперь мы будем использовать скорректированный выигрыш в качестве оценки элемента A (advantage) в функции потерь.
Реализация алгоритма
Импортируем библиотеки и загрузим среду задачи Cart-Pole:
Агент. Сначала создадим функцию, которая будет дисконтировать все последующие выигрыши на текущий момент:
Теперь создадим нашего агента:
Обучение агента. Теперь, наконец, перейдем к обучению агента:
Полный Jupyter Notebook вы можете посмотреть тут. Увидимся в следующих статьях, где мы продолжим изучать обучение с подкреплением!
Обучение с подкреплением
| Определение: |
| Обучение с подкреплением (англ. reinforcement learning) — способ машинного обучения, при котором система обучается, взаимодействуя с некоторой средой. |
Содержание
Обучение с подкреплением [ править ]
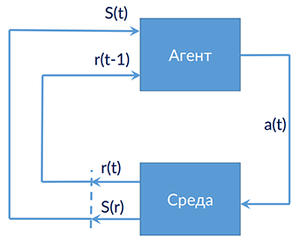
В обучении с подкреплением существует агент (agent) взаимодействует с окружающей средой (environment), предпринимая действия (actions). Окружающая среда дает награду (reward) за эти действия, а агент продолжает их предпринимать.
Алгоритмы с частичным обучением пытаются найти стратегию, приписывающую состояниям (states) окружающей среды действия, одно из которых может выбрать агент в этих состояниях.
Среда обычно формулируется как марковский процесс принятия решений (МППР) с конечным множеством состояний, и в этом смысле алгоритмы обучения с подкреплением тесно связаны с динамическим программированием. Вероятности выигрышей и перехода состояний в МППР обычно являются величинами случайными, но стационарными в рамках задачи.
При обучении с подкреплением, в отличии от обучения с учителем, не предоставляются верные пары «входные данные-ответ», а принятие субоптимальнх решений (дающих локальный экстремум) не ограничивается явно. Обучение с подкреплением пытается найти компромисс между исследованием неизученных областей и применением имеющихся знаний (exploration vs exploitation). Баланс изучения-применения при обучении с подкреплением исследуется в задаче о многоруком бандите.
Формально простейшая модель обучения с подкреплением состоит из:
для МППР без терминальных состояний (где [math]0 \leq \gamma \leq 1[/math] — дисконтирующий множитель для «предстоящего выигрыша»).
Таким образом, обучение с подкреплением особенно хорошо подходит для решения задач, связанных с выбором между долгосрочной и краткосрочной выгодой.
Постановка задачи обучения с подкреплением [ править ]
[math]S[/math] — множество состояний среды
Игра агента со средой:
Алгоритмы [ править ]
Теперь, когда была определена функция выигрыша, нужно определить алгоритм, который будет использоваться для нахождения стратегии, обеспечивающей наилучший результат.
Наивный подход к решению этой задачи подразумевает следующие шаги:
Первая проблема такого подхода заключается в том, что количество доступных стратегий может быть очень велико или бесконечно. Вторая проблема возникает, если выигрыши стохастические — чтобы точно оценить выигрыш от каждой стратегии потребуется многократно применить каждую из них. Этих проблем можно избежать, если допустить некоторую структуризацию и, возможно, позволить результатам, полученным от пробы одной стратегии, влиять на оценку для другой. Двумя основными подходами для реализации этих идей являются оценка функций полезности и прямая оптимизация стратегий.
Поэтому построение искомой оценки при [math]\gamma \in (0, 1)[/math] неочевидно. Однако, можно заметить, что [math]R[/math] образуют рекурсивное уравнение Беллмана:
Подставляя имеющиеся оценки [math]V[/math] и применяя метод градиентного спуска с квадратичной функцией ошибок, мы приходим к алгоритму обучения с временными воздействиями (temporal difference (TD) learning). В простейшем случае и состояния, и действия дискретны и можно придерживаться табличных оценок для каждого состояния.
Другие похожие методы: Адаптивный эвристический критик (Adaptive Heuristic Critic, AHC), SARSA и Q-обучение (Q-learning).
Задача о многоруком бандите (The multi-armed bandit problem) [ править ]
Формулировка [ править ]
[math]A[/math] — множество возможных действий (ручек автомата),
Игра агента со средой:
Выбор действия [math]a_t[/math] на шаге [math]t[/math] влечет награду [math]R(a_t)[/math] при этом [math]R(a)[/math] [math]\forall a \in A[/math] есть случайная величина, распределение которой неизвестно.
Состояние среды у нас от шага к шагу не меняется, а значит множество состояний [math]S[/math] тривиально, ни на что не влияет, поэтому его можно проигнорировать.
Для простоты будем полагать, что каждому действию соответствует некоторое распределение, которое не меняется со временем. Если бы мы знали эти распределения, то очевидная стратегия заключалась бы в том, чтобы подсчитать математическое ожидание для каждого из распределений, выбрать действие с максимальным математическим ожиданием и теперь совершать это действие на каждом шаге.
Задача является модельной для понимания конфликта между exploitation—exploration.
Жадная (greedy) стратегия [ править ]
На каждом шаге [math]t[/math]
В данном случае достаточно попробовать в начале каждую из ручек вместо того, чтобы фокусироваться только на одной. Но если награда случайная величина, то единичной попытки будет не достаточно. Поэтому модифицируем жадную стратегию следующим образом:
На каждом шаге [math]t[/math]
Стратегия Softmax [ править ]
[math]\tau \in (0, \infty)[/math] — параметр, с помощью которого можно настраивать поведение алгоритма.
При [math]\tau \rightarrow \infty[/math] стратегия стремится к равномерной, то есть softmax будет меньше зависеть от значения выигрыша и выбирать действия более равномерно (exploration).
При [math]\tau \rightarrow 0[/math] стратегия стремится к жадной, то есть алгоритм будет больше ориентироваться на известный средний выигрыш действий (exploitation).
Экспонента используется для того, чтобы данный вес был ненулевым даже у действий, награда от которых пока нулевая.
Эвристика: параметр [math]\tau[/math] имеет смысл уменьшать со временем.
Метод UCB (upper confidence bound) [ править ]
Предыдущие алгоритмы при принятии решения используют данные о среднем выигрыше. Проблема в том, что если действие даёт награду с какой-то вероятностью, то данные от наблюдений получаются шумные и мы можем неправильно определять самое выгодное действие.
Алгоритм верхнего доверительного интервала (upper confidence bound или UCB) — семейство алгоритмов, которые пытаются решить эту проблему, используя при выборе данные не только о среднем выигрыше, но и о том, насколько можно доверять значениям выигрыша.
Также как softmax в UCB при выборе действия используется весовой коэффициент, который представляет собой верхнюю границу доверительного интервала (upper confidence bound) значения выигрыша:
[math]b_a = \sqrt<\frac<2 \ln<\sum_a P_a>>
В отличие от предыдущих алгоритмов UCB не использует в своей работе ни случайные числа для выбора действия, ни параметры, которыми можно влиять на его работу. В начале работы алгоритма каждое из действий выбирается по одному разу (для того чтобы можно было вычислить размер бонуса для всех действий). После этого в каждый момент времени выбирается действие с максимальным значением весового коэффициента.
Несмотря на это отсутствие случайности результаты работы этого алгоритма выглядят довольно шумно по сравнению с остальными. Это происходит из-за того, что данный алгоритм сравнительно часто выбирает недоисследованные действия.
Q-learning [ править ]
Таким образом, алгоритм это функция качества от состояния и действия:
Введение в обучение с подкреплением
Мы открыли новый поток на курс «Machine learning», так что ждите в ближайшее время статей связанных с данной, так сказать, дисциплиной. Ну и разумеется открытых семинаров. А сейчас давайте рассмотрим, что такое обучение с подкреплением.
Обучение с подкреплением является важным видом машинного обучения, где агент учится вести себя в окружающей среде, выполняя действия и видя результаты.
В последние годы мы наблюдаем много успехов в этой увлекательной области исследований. Например, DeepMind и Deep Q Learning Architecture в 2014 году, победа над чемпионом по игре в го с AlphaGo в 2016, OpenAI и PPO в 2017 году, среди прочих.
В этой серии статей мы сосредоточимся на изучении различных архитектур, используемых сегодня для решения задачи обучения с подкреплением. К ним относятся Q-learning, Deep Q-learning, Policy Gradients, Actor Critic и PPO.
В этой статье вы узнаете:
Идея обучения с подкреплением заключается в том, что агент будет учиться у окружающей среды, взаимодействуя с ней и получая вознаграждения за выполнение действий.
Обучение через взаимодействие с окружающей средой происходит из нашего естественного опыта. Представьте, что вы ребенок в гостиной. Вы видите камин и подходите к нему.
Рядом тепло, вы чувствуете себя хорошо (положительное вознаграждение +1). Вы понимаете, что огонь — это положительная вещь.
Именно так люди учатся через взаимодействие. Обучение с подкреплением — это просто вычислительный подход к обучению через действия.
Процесс обучения с подкреплением
В качестве примера представим, что агент учится играть в Super Mario Bros. Процесс обучения с подкреплением (Reinforcement Learning — RL) можно смоделировать как цикл, который работает следующим образом:
Центральная идея Гипотезы вознаграждения
Почему цель агента заключается в максимизации ожидаемого накопленного вознаграждения? Ну, обучение с подкреплением основано на идее гипотезы вознаграждения. Все цели можно описать максимизацией ожидаемого накопленного вознаграждения.
Поэтому в обучении с подкреплением, чтобы добиться наилучшего поведения, нам нужно максимизировать ожидаемое накопленное вознаграждение.
Накопленное вознаграждение на каждом временном шаге t может быть записано как:
Однако на самом деле мы не можем просто прибавлять такие вознаграждения. Вознаграждения, которые поступают раньше (в начале игры), более вероятны, поскольку они более предсказуемы, чем вознаграждения в дальнейшей перспективе.
Допустим, что ваш агент — это маленькая мышь, а оппонент — кошка. Ваша цель — съесть максимальное количество сыра, прежде чем кошка вас съест. Как мы видим на диаграмме, мышь вероятнее съест сыр рядом с собой, чем сыр около кошки (чем ближе мы находимся к ней, тем это опаснее).
Как следствие, вознаграждение у кошки, даже если оно больше (больше сыра), будет снижено. Мы не уверены, что сможем его съесть. Чтобы снизить вознаграждение, мы делаем следующее:
Грубо говоря, каждое вознаграждение будет снижено с помощью гаммы к показателю времени. По мере увеличения временного шага кошка становится ближе к нам, поэтому будущая награда становится все менее вероятной.
Эпизодические или непрерывные задачи
Задача — это экземпляр проблемы обучения с подкреплением. У нас могут быть два типа задач: эпизодическая и непрерывная.
В этом случае мы имеем начальную точку и конечную точку (терминальное состояние). Это создает эпизод: список состояний, действий, вознаграждений и новых состояний.
Возьмем к примеру Super Mario Bros: эпизод начинается с запуска нового Марио и заканчивается, когда вы убиты или достигнете конца уровня.

Начало нового эпизода
Это задачи, которые продолжаются вечно (без терминального состояния). В этом случае агент должен научиться выбирать лучшие действия и одновременно взаимодействовать с окружающей средой.
Например, агент, который выполняет автоматическую торговлю акциями. Для этой задачи нет начальной точки и терминального состояния. Агент продолжает работать, пока мы не решим его остановить.
Метод Монте-Карло против метода временных различий
Есть два способа обучения:
Когда эпизод заканчивается (агент достигает «терминального состояния»), агент просматривает общее накопленное вознаграждение, чтобы увидеть, насколько хорошо он справился. В подходе Монте-Карло вознаграждение получается только в конце игры.
Затем мы начинаем новую игру с дополненными знаниями. Агент принимает лучшие решения с каждой итерацией.
Если мы возьмем лабиринт в качестве окружающей среды:
Временные различия: обучение на каждом временном шаге
Метод временных различий (TD — Temporal Difference Learning) не будет ждать конца эпизода, чтобы обновить максимально возможное вознаграждение. Он будет обновлять V в зависимости от полученного опыта.
Этот метод называется TD(0) или пошаговый TD (обновляет функцию полезности после любого отдельного шага).
TD-методы ожидают только следующего временного шага для обновления значений. В момент времени t + 1 формируется TD цель с использованием вознаграждения Rt+1 и текущей оценки V(St+1).
TD цель — это оценка ожидаемого: фактически вы обновляете предыдущую оценку V(St) к цели в пределах одного шага.
Прежде чем рассматривать различные стратегии решения задач обучения с подкреплением, мы должны рассмотреть еще одну очень важную тему: компромисс между разведкой и эксплуатацией.
В этой игре у нашей мыши может быть бесконечное количество маленьких кусочков сыра (+1 каждый). Но на вершине лабиринта есть гигантский кусок сыра (+1000). Однако, если мы сосредоточимся только на вознаграждении, наш агент никогда не достигнет гигантского куска. Вместо этого он будет использовать только ближайший источник вознаграждений, даже если этот источник небольшой (эксплуатация). Но если наш агент немного разведает обстановку, он сможет найти большое вознаграждение.
Это то, что мы называем компромиссом между разведкой и эксплуатацией. Мы должны определить правило, которое поможет справиться с этим компромиссом. В будущих статьях вы узнаете разные способы это сделать.
Три подхода к обучению с подкреплением
Теперь, когда мы определили основные элементы обучения с подкреплением, давайте перейдем к трем подходам решения задач обучения с подкреплением: на основе стоимости, на основе политике и на основе модели.
На основе стоимости
В RL на основе стоимости, целью является оптимизация функции полезности V(s).
Функция полезности — это функция, которая сообщает нам о максимальном ожидаемом вознаграждении, которое агент получит в каждом состоянии.
Значение каждого состояния — это общая сумма вознаграждения, которое агент может рассчитывать накопить в будущем, начиная с этого состояния.
Агент будет использовать эту функцию полезности, чтобы решить, какое состояние выбрать на каждом шаге. Агент выбирает состояние с наибольшим значением.
На основе политики
В RL на основе политики мы хотим напрямую оптимизировать функцию политики π(s) без использования функции полезности. Политикой является то, что определяет поведение агента в данный момент времени.

действие = политика(состояние)
Мы изучаем функцию политики. Это позволяет нам сопоставить каждое состояние с наилучшим соответствующим действием.
Есть два типа политики:
Как можно заметить, политика прямо указывает на лучшее действие для каждого шага.
В RL на основе модели мы моделируем среду. Это означает, что мы создаем модель поведения окружающей среды. Проблема заключается в том, что каждой среде потребуется другое представление модели. Вот почему мы не будем сильно заострять внимание на этом типе обучения в следующих статьях.
Знакомство с глубоким обучением с подкреплением
Глубокое обучение с подкреплением (Deep Reinforcement Learning) вводит глубокие нейронные сети для решения задач обучения с подкреплением — отсюда и название «глубокое».
Например, в следующей статье мы будем работать над Q-Learning (классическое обучение с подкреплением) и Deep Q-Learning.
Вы увидите разницу в том, что в первом подходе мы используем традиционный алгоритм для создания таблицы Q, которая помогает нам найти, какое действие нужно предпринять для каждого состояния.
Во втором подходе мы будем использовать нейронную сеть (для аппроксимации вознаграждения на основе состояния: значение q).

Схема, вдохновленная учебным пособием Q от Udacity
Вот и всё. Как всегда мы ждём ваши комментарии или вопросы тут или их можно задать преподавателю курса Артуру Кадурину на его открытом уроке, посвящённому обучению сетей.