график обучения нейронной сети
Визуализация процесса обучения нейронной сети средствами TensorFlowKit
Начиная работать в сфере машинного обучения, мне было тяжело переходить от объектов и их поведений к векторам и пространствам. Сперва все это достаточно тяжело укладывалось в голове и далеко не все процессы казались прозрачными и понятными с первого взгляда. По этой причине все, что происходило внутри моих наработок, я пробовал визуализировать: строил 3D модели, графики, диаграммы, изображения и тд.
Говоря об эффективной разработке систем машинного обучения, всегда поднимается вопрос контроля скорости обучения, анализа процесса обучения, сбора различных метрик обучения и тд. Особая сложность заключается в том, что мы (люди) привыкли оперировать 2х и 3х мерными пространствами, описывая различные процессы вокруг нас. Процессы внутри нейронных сетей происходят в многомерных пространствах, что серьезно усложняет их понимание. Осознавая это, инженеры по всему миру стараются разработать различные подходы к визуализации или трансформации многомерных данных в более простые и понятные формы.
Существуют целые сообщества, решающие такого рода задачи, например Distill, Welch Labs, 3Blue1Brown.
TensorBoard
Еще до начала работы с TensorFlow я начал работать с TensorBoard пакетом. Оказалось, что это очень удобное, кросплатформенное решение для визуализации разного рода данных. Потребовалось пару дней, чтоб “научить” swift приложение создавать отчеты в формате TensorBoard и интегрировать в мою нейронную сеть.
Разработка TensorBoard началась еще в середине 2015 года в рамках одной из лабораторий Google. В конце 2015го Google открыл исходный код и работа над проектом стала публичной.
Текущая версия TensorBoard — это python пакет, созданный в помощь TensorFlow, который позволяет визуализировать несколько типов данных:
Для работы нам понадобится TensorBoard на нашем компьютере (Ubuntu или Mac). У нас должен быть установлен python3. Я советую установить TensorBoard как часть TensorFlow пакета для python.
Запускаем TensorBoard, указав папку в которой мы будем хранить отчеты:
TensorFlowKit
Пример на GitHub
Не забудьте поставить «start» репозиторию.
Рассмотрим несколько случаев уже непосредственно на примере. Создание отчетов (summary) в формате TensorBoard происходит в момент конструирования графа вычислений. В TensorFlowKit я постарался максимально повторить python подходы и интерфейс, чтобы в дальнейшем можно было пользоваться общей документацией.
Как я уже сказал выше, каждый наш отчет мы собираем в summary. Это контейнер, в котором хранится массив value, каждый из которых представляет какое — либо событие, которое мы хотим визуализировать.
Summary в дальнейшем будет сохранен в файл на файловой системе, где его и прочтет TensorBoard.
Таким образом, нам необходимо создать FileWriter, указав граф, который мы хотим визуализировать и создать Summary, в который мы будем складывать наши значения.
Запустив приложение и обновив страницу, мы уже можем видеть граф, который мы создали в коде. Он будет интерактивен, так что по нему можно перемещаться.
Далее, мы хотим видеть изменение некой скалярной величины во времени, например значение функции потерь (loss function or cost function) и accuracy нашей нейронной сети. Для этого добавляем выходы наших операций в summary:
Таким образом, после каждого шага вычислений нашей сессии, TensorFlow автоматически вычитает значения наших операций и передаст их на вход результирующего Summary, который мы сохраним в FileWriter (как это сделать я опишу ниже).
Также у нас в нейросети есть большее количество весов и предубеждений (bias). Как правило это различные матрицы достаточно большой размерности и анализировать их значения распечатывая крайне сложно. Будет лучше, если мы построим график распределений (distribution). Добавим в наш Summary еще и информацию о величине изменений весов, которую проделывает наша сеть после каждого шага обучения.
Теперь в нашем распоряжении визуализация того, как менялись веса и какими были изменения во время обучения.
Но это еще не все. Давайте действительно заглянем в устройство нашей нейронной сети.
Каждая картинка рукописного текста, полученная на вход, находит некое отражение в соответствующих ей весах. То есть, поданная на вход картинка умеет активировать определенные нейроны, тем самым имеет некий отпечаток внутри нашей сети. Напомню, что мы имеем 784 веса на каждый нейрон из 10. Таким образом, у нас 7840 весов. Все они представлены в виде матрицы 784×10. Попробуем развернуть всю матрицу в вектор и после этого “вытащить” веса, которые относятся к каждому отдельному классу:
Для этого добавим в граф еще несколько операций stridedSlice и reshape. Теперь, каждый полученный вектор добавим в Summary как картинку:
В разделе Images в TensorBoard мы теперь видим “отпечатки” весов, такими какими они были во время процесса обучения.
Осталось только обработать наш Summary. Для этого нам надо соединить все созданные Summary в один и обработать его во время обучения сети.
В момент работы нашей сети:
Прошу обратить внимание, что в этом примере я не рассматриваю вопрос вычисления accuracy, он вычисляется на данных обучения. Вычислять его на данных для обучения неверно.
В следующей статье я постараюсь рассказать, как собрать одну нейросеть и запустить ее на Ubuntu, MacOS, iOS из одного репозитория.
Как работает нейронная сеть: алгоритмы, обучение, функции активации и потери
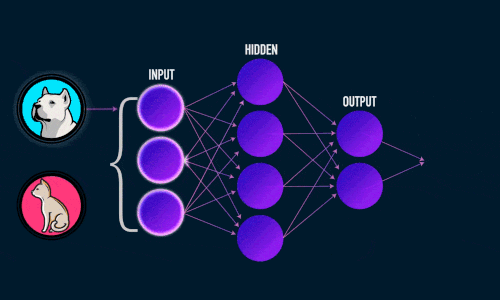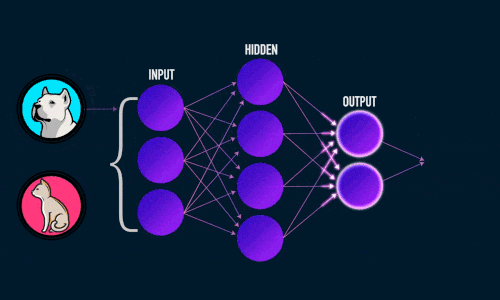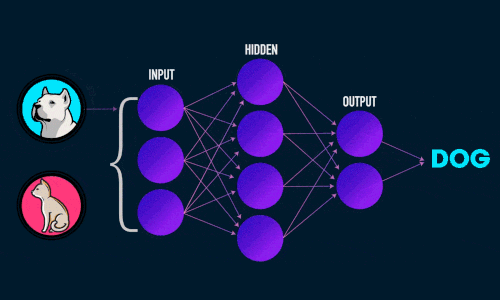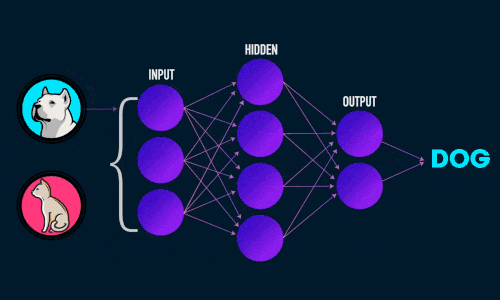
Нейронная сеть — попытка с помощью математических моделей воспроизвести работу человеческого мозга для создания машин, обладающих искусственным интеллектом.
Искусственная нейронная сеть обычно обучается с учителем. Это означает наличие обучающего набора (датасета), который содержит примеры с истинными значениями: тегами, классами, показателями.
Неразмеченные наборы также используют для обучения нейронных сетей, но мы не будем здесь это рассматривать.
Например, если вы хотите создать нейросеть для оценки тональности текста, датасетом будет список предложений с соответствующими каждому эмоциональными оценками. Тональность текста определяют признаки (слова, фразы, структура предложения), которые придают негативную или позитивную окраску. Веса признаков в итоговой оценке тональности текста (позитивный, негативный, нейтральный) зависят от математической функции, которая вычисляется во время обучения нейронной сети.
Раньше люди генерировали признаки вручную. Чем больше признаков и точнее подобраны веса, тем точнее ответ. Нейронная сеть автоматизировала этот процесс.
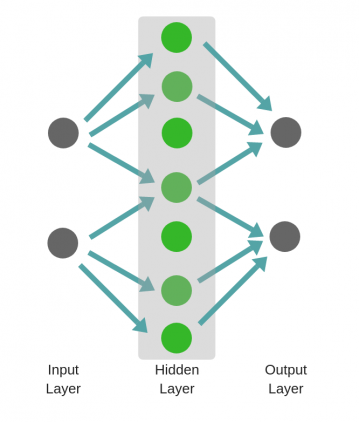
Искусственная нейронная сеть состоит из трех компонентов:
Обучение нейросетей происходит в два этапа:
Во время прямого распространения ошибки делается предсказание ответа. При обратном распространении ошибка между фактическим ответом и предсказанным минимизируется.
Прямое распространение ошибки
Зададим начальные веса случайным образом:
Умножим входные данные на веса для формирования скрытого слоя:
Выходные данные из скрытого слоя передается через нелинейную функцию (функцию активации), для получения выхода сети:
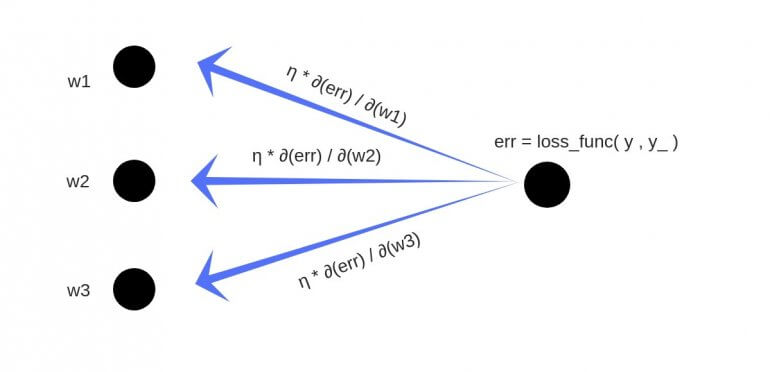
Обратное распространение
Полученный результат затем вычитается из соответствующих весов.
В результате получатся следующие обновленные веса:
То, что мы предполагаем и инициализируем веса случайным образом, и они будут давать точные ответы, звучит не вполне обоснованно, тем не менее, работает хорошо.

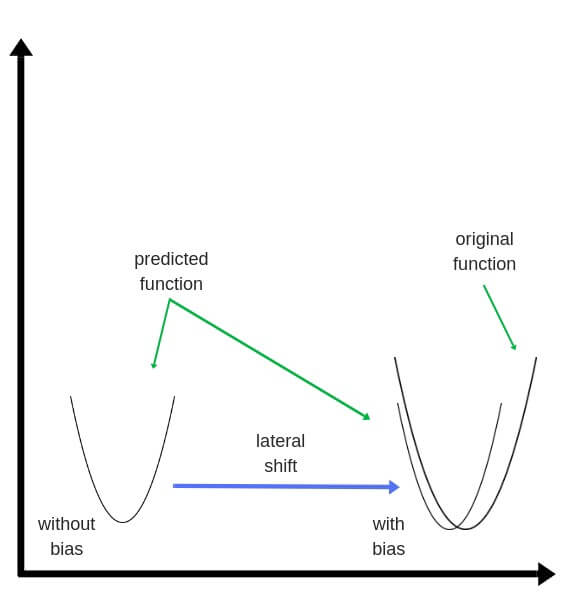
Смещения – это веса, добавленные к скрытым слоям. Они тоже случайным образом инициализируются и обновляются так же, как скрытый слой. Роль скрытого слоя заключается в том, чтобы определить форму базовой функции в данных, в то время как роль смещения – сдвинуть найденную функцию в сторону так, чтобы она частично совпала с исходной функцией.
Частные производные
Частные производные можно вычислить, поэтому известно, какой был вклад в ошибку по каждому весу. Необходимость производных очевидна. Представьте нейронную сеть, пытающуюся найти оптимальную скорость беспилотного автомобиля. Eсли машина обнаружит, что она едет быстрее или медленнее требуемой скорости, нейронная сеть будет менять скорость, ускоряя или замедляя автомобиль. Что при этом ускоряется/замедляется? Производные скорости.
Разберем необходимость частных производных на примере.
Предположим, детей попросили бросить дротик в мишень, целясь в центр. Вот результаты:
Теперь, если мы найдем общую ошибку и просто вычтем ее из всех весов, мы обобщим ошибки, допущенные каждым. Итак, скажем, ребенок попал слишком низко, но мы просим всех детей стремиться попадать в цель, тогда это приведет к следующей картине:
Ошибка нескольких детей может уменьшиться, но общая ошибка все еще увеличивается.
Найдя частные производные, мы узнаем ошибки, соответствующие каждому весу в отдельности. Если выборочно исправить веса, можно получить следующее:
Гиперпараметры
Нейронная сеть используется для автоматизации отбора признаков, но некоторые параметры настраиваются вручную.
Скорость обучения (learning rate)
Скорость обучения является очень важным гиперпараметром. Если скорость обучения слишком мала, то даже после обучения нейронной сети в течение длительного времени она будет далека от оптимальных результатов. Результаты будут выглядеть примерно так:
С другой стороны, если скорость обучения слишком высока, то сеть очень быстро выдаст ответы. Получится следующее:
Функция активации (activation function)
Функция активации — это один из самых мощных инструментов, который влияет на силу, приписываемую нейронным сетям. Отчасти, она определяет, какие нейроны будут активированы, другими словами и какая информация будет передаваться последующим слоям.
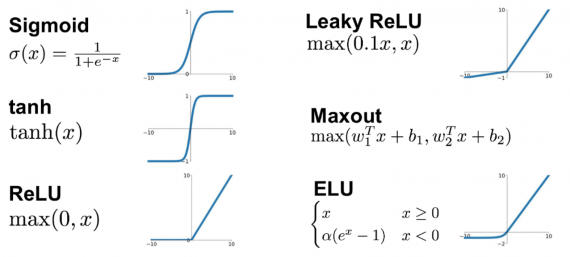
Без функций активации глубокие сети теряют значительную часть своей способности к обучению. Нелинейность этих функций отвечает за повышение степени свободы, что позволяет обобщать проблемы высокой размерности в более низких измерениях. Ниже приведены примеры распространенных функций активации:
Функция потери (loss function)
Функция потерь находится в центре нейронной сети. Она используется для расчета ошибки между реальными и полученными ответами. Наша глобальная цель — минимизировать эту ошибку. Таким образом, функция потерь эффективно приближает обучение нейронной сети к этой цели.
Функция потерь измеряет «насколько хороша» нейронная сеть в отношении данной обучающей выборки и ожидаемых ответов. Она также может зависеть от таких переменных, как веса и смещения.
Функция потерь одномерна и не является вектором, поскольку она оценивает, насколько хорошо нейронная сеть работает в целом.
Некоторые известные функции потерь:
Cреднеквадратичное отклонение – самая простая фукция потерь и наиболее часто используемая. Она задается следующим образом:
Функция потерь в нейронной сети должна удовлетворять двум условиям:
Глубокие нейронные сети
Глубокое обучение (deep learning) – это класс алгоритмов машинного обучения, которые учатся глубже (более абстрактно) понимать данные. Популярные алгоритмы нейронных сетей глубокого обучения представлены на схеме ниже.
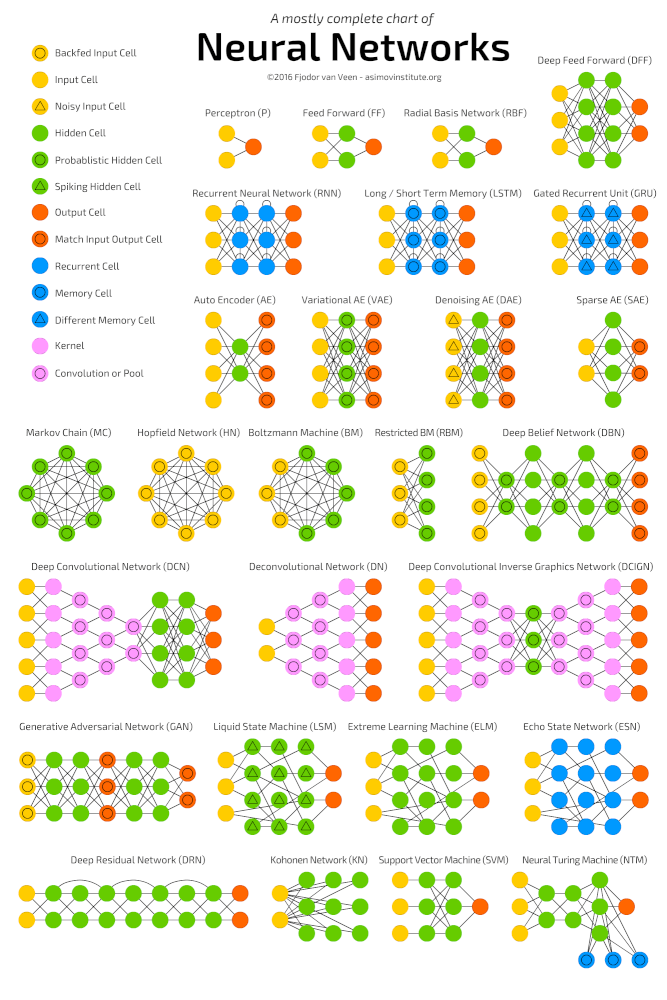
Более формально в deep learning:
Пример
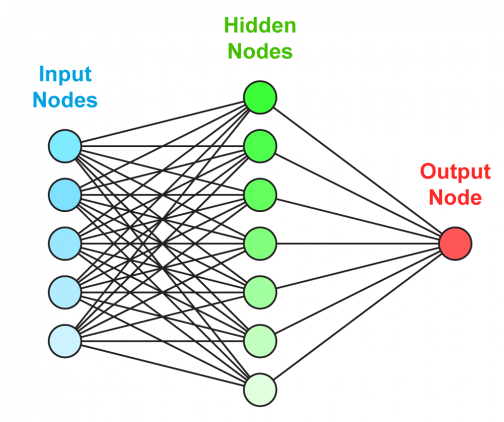
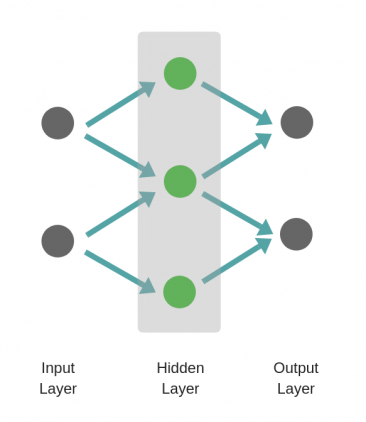
Рассмотрим однослойную нейронную сеть:
Здесь, обучается первый слой (зеленые нейроны), он просто передается на выход.
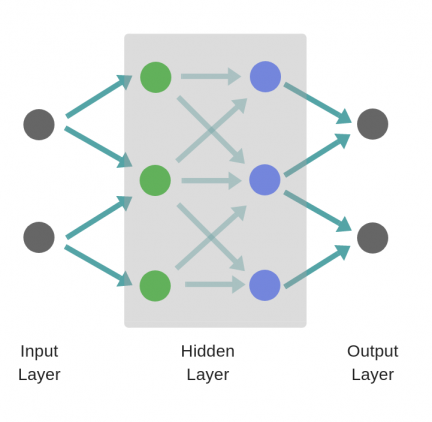
В то время как в случае двухслойной нейронной сети, независимо от того, как обучается зеленый скрытый слой, он затем передается на синий скрытый слой, где продолжает обучаться:
Следовательно, чем больше число скрытых слоев, тем больше возможности обучения сети.
Не следует путать с широкой нейронной сетью.
В этом случае большое число нейронов в одном слое не приводит к глубокому пониманию данных. Но это приводит к изучению большего числа признаков.
Изучая английскую грамматику, требуется знать огромное число понятий. В этом случае однослойная широкая нейронная сеть работает намного лучше, чем глубокая нейронная сеть, которая значительно меньше.
В случае изучения преобразования Фурье, ученик (нейронная сеть) должен быть глубоким, потому что не так много понятий, которые нужно знать, но каждое из них достаточно сложное и требует глубокого понимания.
Главное — баланс
Очень заманчиво использовать глубокие и широкие нейронные сети для каждой задачи. Но это может быть плохой идеей, потому что:
Проклятье размерности
Проклятие размерности относится к различным явлениям, возникающим при анализе и организации данных в многомерных пространствах (часто с сотнями или тысячами измерений), и не встречается в ситуациях с низкой размерностью.
Грамматика английского языка имеет огромное количество аттрибутов, влияющих на нее. В машинном обучении мы должны представить их признаками в виде массива/матрицы конечной и существенно меньшей длины (чем количество существующих признаков). Для этого сети обобщают эти признаки. Это порождает две проблемы:
Компромисс
На ранней стадии обучения смещение велико, потому что выход из сети далек от желаемого. А дисперсия очень мала, поскольку данные имеет пока малое влияние.
В конце обучения смещение невелико, потому что сеть выявила основную функцию в данных. Однако, если обучение слишком продолжительное, сеть также изучит шум, характерный для этого набора данных. Это приводит к большому разбросу результатов при тестировании на разных множествах, поскольку шум меняется от одного набора данных к другому.
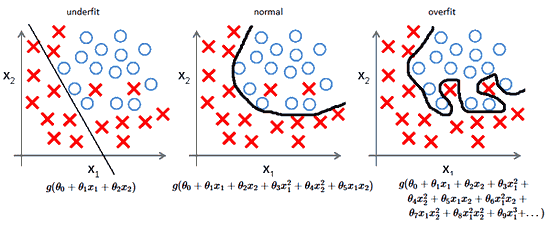
алгоритмы с большим смещением обычно в основе более простых моделей, которые не склонны к переобучению, но могут недообучиться и не выявить важные закономерности или свойства признаков. Модели с маленьким смещением и большой дисперсией обычно более сложны с точки зрения их структуры, что позволяет им более точно представлять обучающий набор. Однако они могут отображать много шума из обучающего набора, что делает их прогнозы менее точными, несмотря на их дополнительную сложность.
Следовательно, как правило, невозможно иметь маленькое смещение и маленькую дисперсию одновременно.
Сейчас есть множество инструментов, с помощью которых можно легко создать сложные модели машинного обучения, переобучение занимает центральное место. Поскольку смещение появляется, когда сеть не получает достаточно информации. Но чем больше примеров, тем больше появляется вариантов зависимостей и изменчивостей в этих корреляциях.
Стэнфордский курс: лекция 6. Обучение нейросетей, часть 1
В прошлый раз мы обсудили историю возникновения свёрточных архитектур, а также узнали об их устройстве и широких возможностях применения. В течение следующих двух лекций мы поговорим об особенностях обучения нейросетей и разберёмся, как правильно настраивать параметры, выбирать функцию активации, подготавливать данные и добиваться успешных результатов.
Обучение нейросети — непредсказуемый и захватывающий процесс, который, однако, требует тщательной подготовки. В целом его можно разделить на три основных этапа:
В этой лекции мы обсудим некоторые детали первых двух пунктов. Если вы уже знакомы со всеми понятиями и имеете опыт работы с нейросетями, рекомендуем нашу статью с полезными советами по обучению моделей.
Обучение нейросети — непредсказуемый и захватывающий процесс, который, однако, требует тщательной подготовки. В целом его можно разделить на три основных этапа:
Сюда входят: выбор функции активации, предварительная обработка данных, инициализация весов, регуляризация, градиентная проверка.
Отслеживание процесса обучения, оптимизация и обновление гиперпараметров.
В этой лекции мы обсудим некоторые детали первых двух пунктов. Если вы уже знакомы со всеми понятиями и имеете опыт работы с нейросетями, рекомендуем нашу статью с полезными советами по обучению моделей.
Функция активации
Ранее мы выяснили, что в каждый слой нейросети поступают входные данные. Они умножаются на веса полносвязного или свёрточного слоя, а результат передаётся в функцию активации или нелинейность. Мы также говорили о сигмоиде и ReLU, которые часто используются в качестве таких функций. Но список возможных вариантов не ограничивается только ими. Какой же следует выбирать?
Рассмотрим наиболее популярные функции активации и обсудим их преимущества и недостатки.
Сигмоида
Функция сигмоиды преобразовывает поступающие в неё значения в вещественный диапазон [0, 1]. То есть, если входные данные окажутся большими положительными значениями, то после преобразования они будут равны примерно единице, а отрицательные числа станут близки к нулю. Это довольно популярная функция, которую можно интерпретировать как частоту возбуждения нейрона.
Но если внимательнее присмотреться к сигмоиде, можно заметить несколько проблем.
1. Насыщенные нейроны могут «убить» градиент. Возьмём сигмоидный узел вычислительного графа и передадим в него входные данные X. Когда мы делаем обратный проход, восходящий градиент равен dL/d𝜎, а локальный — dL/d𝜎 * d𝜎/dx.
Что же произойдёт, если X будет равен −10? Градиент станет нулевым, поскольку все большие отрицательные значения находятся на прямом участке сигмоидной функции. Таким образом, во все последующие узлы будут передаваться нулевые производные — это и «убивает» градиентный поток.
А если X = 0? В этом случае всё будет в порядке, как и для других близких к нулю значений. А вот при X = 10 градиент снова обнулится. Поэтому сигмоида не работает для слишком высоких положительных или отрицательных данных.
2. Выходные значения сигмоиды не центрированы нулем. Пусть исходные данные полностью положительны — что тогда станет с градиентами во время обратного распространения? Они все будут либо положительными, либо отрицательными (в зависимости от градиента f). Это приведёт к тому, что все веса при обновлении также будут либо увеличены, либо уменьшены, и градиентный поток станет зигзагообразным.
Поэтому следует изначально подготавливать данные таким образом, чтобы их средним значением являлся ноль.
3. Функцию exp() достаточно дорого считать. Это не такая существенная проблема, поскольку скалярные произведения во время свёртки тратят гораздо больше вычислительных мощностей, но в сравнении с остальными функциями активации её тоже можно отметить.
Тангенс
Тангенс очень похож на сигмоиду, но обладает двумя существенными отличиями: он преобразует данные в диапазон [-1, 1] и имеет нулевое центрирование, что исключает вторую проблему сигмоиды. Значения градиента при обратном распространении по-прежнему могут обнуляться, тем не менее, использование тангенса обычно более предпочтительно.
ReLU
ReLU или Rectified Linear Unit стала довольно популярной в последние годы. Она вычисляет функцию f(x) = max(0,x), то есть просто выдаёт значения «ноль» и «не ноль». Это решает проблему обнуления градиента для положительных чисел. Кроме того, ReLU очень просто вычисляется: примерно в шесть раз быстрее сигмоиды и тангенса. Однако, в ней снова отсутствует нулевое центрирование.
Другой очевидный недостаток — градиент по-прежнему «умирает» при отрицательных входных данных. Это может привести к тому, что половина нейронов будет неактивна и не сможет обновляться.
Проблему можно попробовать решить, задав более низкую скорость обучения и подобрав другие весовые коэффициенты. Или использовать модификации ReLU.
Leaky ReLU
Отличие этой функции в том, что она имеет небольшой наклон в левой полуплоскости — значит, при отрицательных входных данных градиент не будет нулевым.
При этом функцию по-прежнему легко вычислить. То есть, она решает практически все перечисленные проблемы. Одной из её разновидностей является PReLU, которая выглядит как f(x) = max(𝛼x, x).
ELU
Эта функция похожа на leaky ReLU и обладает всеми её преимуществами, но включает в себя экспоненту, что делает её вычисление дороже. Её стоит использовать в тех случаях, когда вам важна устойчивость к шумовым данным.
Maxout
Maxout выбирает максимальную сумму из двух наборов весов, умноженных на исходные данные с учётом смещения. Тем самым он обобщает ReLU и leaky ReLU, не обнуляя градиент. Но, как можно догадаться по виду функции, maxout требует удвоения параметров и нейронов.
Подводя итог: используйте ReLU, можете попробовать взять leaky ReLU/Maxout/ELU. На тангенс и сигмоиду лучше не рассчитывать.
Подготовка данных
Существует три наиболее распространённых способа предварительной обработки данных. Будем полагать, что данные X — это матрица размером [NxD].
2. Нормализация. Изменение данных таким образом, чтобы они все были приблизительно одного масштаба. Один из вариантов — разделить каждое измерение на его стандартное отклонение: (X /= np.std(X, axis = 0)). Другой вариант — нормализовать каждое значение так, чтобы min и max были равны -1 и 1 соответственно. Нормализацию следует применять только в том случае, если исходные данные имеют разные форматы или единицы измерения. У изображений значения пикселей не выходят за пределы диапазона от 0 до 255, поэтому для них нет необходимости выполнять нормализацию.
Инициализация весов
Итак, мы построили архитектуру нейронной сети и подготовили данные. Прежде чем начать обучение, необходимо инициализировать параметры (веса).
Как не нужно делать: задавать веса нулевыми. Это приведёт к тому, что абсолютно все нейроны будут вести себя одинаково — совсем не то, что мы хотим получить. Нейросеть должна обучаться разным признакам.
Небольшие случайные величины. Более удачный вариант — присвоить весам маленькие значения. Тогда все нейроны будут уникальными и в процессе обучения постепенно интегрируются в различные части сети. Реализация может выглядеть так: W = 0.01* np.random.randn(D,H). Метод randn(n) формирует массив размера n х n, элементами которого являются случайные величины, распределённые по нормальному закону с математическим ожиданием 0 и среднеквадратичным отклонением 1 (распределение Гаусса). Недостаток этого способа в том, что он неплохо работает для небольших архитектур, но гораздо хуже справляется с громоздкими нейросетями.
Калибровка с помощью 1/sqrt(n). Проблема вышеупомянутого метода состоит в том, что дисперсия случайных величин растёт с числом нейронов. Чтобы избежать этого, можно масштабировать веса, поделив их на корень из количества входов: w = np.random.randn(n) / sqrt(n). Это гарантирует, что все нейроны сети изначально будут иметь примерно одинаковое выходное распределение.
Также можно использовать вариант w = np.random.randn(n) * sqrt(2.0/n), который был предложен в одном из исследований. Он приводит к наиболее удачному распределению нейронов, поэтому на практике рекомендуем использовать именно его.
Пакетная нормализация
Метод, известный также как batch normalization, решает множество проблем при инициализации, заставляя все активации (выводы) принимать единичное гауссово распределение в начале обучения.
Как же это работает? Рассмотрим небольшое число выводов нейронов на каком-либо слое. Пусть в функцию активации поступает вектор размерности d: x = (x(1),…,x(d)). Нормализуем его по каждой из размерностей:
Где E(x) — математическое ожидание, D(x) — дисперсия, которые вычисляются по всей обучающей выборке. Таким образом, вместо инициализации весов можно использовать эту простую дифференцируемую функцию и получить нормальное распределение на каждом слое.
Пакетная нормализация обычно применяется между слоями (полносвязными или свёрточными) и функциями активации.
Это очень полезный алгоритм, который часто применяется в современном машинном обучении. Нейросети, использующие batch normalization, значительно более устойчивы к плохой инициализации.
За нейросетью глаз да глаз
Мы выбрали архитектуру сети, подготовили данные, инициализировали веса и нормализовали их. Пришло время начать обучение! Вернее, попытаться начать. Самый простой способ проверить, что нейросеть готова обучаться — взять совсем немного данных и попробовать переобучить её на них, то есть, добиться очень хорошей точности и малых потерь. Для этого мы убираем регуляризацию, устанавливаем необходимое количество эпох обучения и вычисляем потери (они должны уменьшаться).
Напомним, что эпоха — один «проход» данных через нейросеть, после которого обновляются веса с помощью градиентного спуска. Упрощённо это выглядит следующим образом:
Теперь можно запустить настоящий процесс: взять все данные, добавить регуляризацию и установить начальную скорость обучения. К сожалению, просто выполнить код и оставить нейросеть на пару часов пока не получится. Необходимо убедиться, что потери постепенно уменьшаются после каждой эпохи. Если этого не происходит, скорее всего, скорость обучения слишком маленькая. Стремительный рост потерь наоборот говорит о слишком высоком значении learning rate.
Оптимизация гиперпараметров
Как мы могли убедиться, обучение нейронных сетей включает множество этапов настройки гиперпараметров. Наиболее распространенными являются:
— начальная скорость обучения;
— график затухания скорости обучения (например, постоянная затухания);
При желании можно даже модернизировать архитектуру сети, если вам кажется, что она выбрана не слишком удачно.
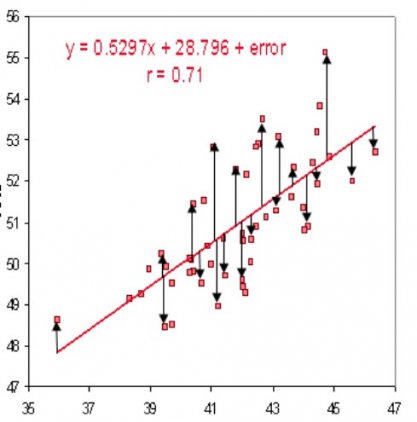
Learning rate — одно из самых важных значений. Попробуйте поэкспериментировать с различными вариантами и построить графики потерь. На рисунке ниже слева показаны эффекты, возникающие при изменении скорости обучения, а справа — типичная функция потерь при обучении небольшой нейросети на наборе данных CIFAR-10.
Вторая важная вещь, которую следует отслеживать — точность сети на обучающих и оценочных данных. Если поместить их на один график, то можно оценить наличие переобучения, о чём свидетельствуют расходящиеся кривые.
Для поиска оптимальных гиперпараметров стоит написать отдельную функцию, которая будет самостоятельно подбирать их и выполнять оптимизацию. При этом лучше использовать не равномерный поиск (известный также как «перебор по сетке»), а случайный — он чаще всего даёт гораздо более удачные результаты.
Итоги
Кратко изложим всё, что мы узнали про обучение нейросетей из сегодняшней лекции:
— используйте функцию активации ReLU;
— выполняйте предварительную обработку данных (для изображений: вычитайте среднее значение);
— масштабируйте веса при инициализации;
— применяйте пакетную нормализацию;
— следите за процессом обучения;
— оптимизируйте гиперпараметры с помощью случайного поиска.
На следующей лекции мы расскажем ещё о нескольких важных шагах обучения, узнаем про ансамблевые методы и разберёмся, как выполнять передачу обучения (transfer learning) и точную настройку (fine tuning). Пробовали ли вы самостоятельно обучать нейросети? Были ли у вас свои хитрости, или вы полагались на установки по умолчанию? Делитесь с нами успехами и не забывайте задавать вопросы, если что-то непонятно.
Следующие лекции (список будет дополняться по мере появления материалов):
С оригинальной лекцией можно ознакомиться на YouTube.