permutation importance машинное обучение
Permutation Importance¶
eli5 provides a way to compute feature importances for any black-box estimator by measuring how score decreases when a feature is not available; the method is also known as “permutation importance” or “Mean Decrease Accuracy (MDA)”.
A similar method is described in Breiman, “Random Forests”, Machine Learning, 45(1), 5-32, 2001 (available online at https://www.stat.berkeley.edu/%7Ebreiman/randomforest2001.pdf).
Algorithm¶
To do that one can remove feature from the dataset, re-train the estimator and check the score. But it requires re-training an estimator for each feature, which can be computationally intensive. Also, it shows what may be important within a dataset, not what is important within a concrete trained model.
The method is most suitable for computing feature importances when a number of columns (features) is not huge; it can be resource-intensive otherwise.
Model Inspection¶
For sklearn-compatible estimators eli5 provides PermutationImportance wrapper. If you want to use this method for other estimators you can either wrap them in sklearn-compatible objects, or use eli5.permutation_importance module which has basic building blocks.
For example, this is how you can check feature importances of sklearn.svm.SVC classifier, which is not supported by eli5 directly when a non-linear kernel is used:
If you don’t have a separate held-out dataset, you can fit PermutationImportance on the same data as used for training; this still allows to inspect the model, but doesn’t show which features are important for generalization.
Feature Selection¶
Note that permutation importance should be used for feature selection with care (like many other feature importance measures). For example, if several features are correlated, and the estimator uses them all equally, permutation importance can be low for all of these features: dropping one of the features may not affect the result, as estimator still has an access to the same information from other features. So if features are dropped based on importance threshold, such correlated features could be dropped all at the same time, regardless of their usefulness. RFE and alike methods (as opposed to single-stage feature selection) can help with this problem to an extent.
Интерпретируемая модель машинного обучения. Часть 1
Всем привет. До старта курса «Machine Learning» остается чуть больше недели. В преддверии начала занятий мы подготовили полезный перевод, который будет интересен как нашим студентам, так и всем читателям блога. Начнем.
Пора избавиться от черных ящиков и укрепить веру в машинное обучение!
В своей книге “Interpretable Machine Learning” Кристоф Мольнар прекрасно выделяет суть интерпретируемости Машинного Обучения с помощью следующего примера: Представьте, что вы эксперт Data Science, и в свободное время пытаетесь спрогнозировать куда ваши друзья отправятся в отпуск летом, основываясь на их данных из facebook и twitter. Итак, если прогноз окажется верным, то ваши друзья будут считать вас волшебником, который может видеть будущее. Если прогнозы будут неверны, то это не принесет вреда ничему, кроме вашей репутации аналитика. Теперь представим, что это был не просто забавный проект, а к нему были привлечены инвестиции. Скажем, вы хотели инвестировать в недвижимость, где ваши друзья, вероятно, будут отдыхать. Что произойдёт, если предсказания модели будут неудачными? Вы потеряете деньги. Пока модель не оказывает существенного влияния, ее интерпретируемость не имеет большого значения, но когда есть финансовые или социальные последствия, связанные с предсказаниями модели, ее интерпретируемость приобретает совершенно другое значение.
Объяснимое машинное обучение
Интерпретировать, значит, объяснить или показать в понятных терминах. В контексте ML-системы, интерпретируемость – это способность объяснить ее действие или показать его в понятном человеку виде.
Модели машинного обучения многие люди окрестили «черными ящиками». Это означает, что несмотря на то, что мы можем получить от них точный прогноз, мы не можем понятно объяснить или понять логику их составления. Но каким образом можно извлечь инсайты из модели? Какие вещи следует иметь в виду и какие инструменты нам понадобятся для этого? Это важные вопросы, которые приходят на ум, когда речь идет об интерпретируемости модели.
Важность интерпретируемости
Вопрос, которым задаются некоторые люди, звучит как, почему бы просто не радоваться тому, что мы получаем конкретный результат работы модели, почему так важно знать, как было принято то или иное решение? Ответ кроется в том, что модель может оказывать определенное влияние на последующие события в реальном мире. Для моделей, которые предназначены для рекомендации фильмов интерпретируемость будет гораздо менее важна, чем для тех моделей, которые используются для прогнозирования результата воздействия медицинского препарата.
«Проблема заключается в том, что всего одна метрика, такая как точность классификации, является недостаточным описанием большинства реальных задач.» (Доши-Велес и Ким 2017)
Вот большая картинка про объяснимое машинное обучение. В каком-то смысле мы захватываем мир (а точнее информацию из него), собирая необработанные данные и используя их для дальнейших прогнозов. По сути, интерпретируемость – это всего лишь еще один слой модели, который помогает людям понять весь процесс.
Некоторые из преимуществ, которые приносит интерпретируемость:
Методы Интерпретации моделей
Теория имеет смысл только до тех пор, пока мы можем применять ее на практике. В случае, если вы действительно хотите разобраться с этой темой, можете попробовать пройти курс Machine Learning Explainability от Kaggle. В нем вы найдете правильное соотношение теории и кода, чтобы понять концепции и уметь применять на практике к реальным кейсам концепции интерпретируемости (объяснимости) моделей.
Нажмите на скриншот ниже, чтобы перейти непосредственно на страницу курса. Если вы хотите сначала получить краткий обзор темы, продолжайте чтение.
Инсайты, которые можно извлечь из моделей
Для понимания модели нам потребуются следующие инсайты:
Давайте обсудим несколько методов, которые помогают извлекать вышеперечисленные инсайты из модели:
Permutation Importance
Какие признаки модель считает важными? Какие признаки оказывают наибольшее влияние? Эта концепция называется важностью признаков (feature importance), а Permutation Importance – это метод, широко используемый для вычисления важности признаков. Он помогает нам увидеть, в какой момент модель выдает неожиданные результаты, он же помогает нам показать другим, что наша модель работает именно так, как нужно.
Permutation Importance работает для многих оценок scikit-learn. Идея проста: Произвольным образом переставить или перетасовать один столбец в наборе датасета валидации, оставив все остальные столбцы нетронутыми. Признак считается «важным», если точность модели падает и его изменение вызывает увеличение ошибок. С другой стороны, признак считается «неважным», если перетасовка его значений не влияет на точность модели.
Как это работает?
Permutation Importance вычисляется с использованием библиотеки ELI5. ELI5 – это библиотека в Python, которая позволяет визуализировать и отлаживать различные модели машинного обучения с помощью унифицированного API. Она имеет встроенную поддержку для нескольких ML-фреймворков и обеспечивает способы интерпретации black-box модели.
Интерпретация
Практика
А теперь, чтобы посмотреть на полный пример и проверить правильно ли вы все поняли, перейдите на страницу Kaggle по ссылке.
Вот и подошла к концу первая часть перевода. Пишите ваши комментарии и дл встречи на курсе!
4.2. Permutation feature importance¶
Features that are deemed of low importance for a bad model (low cross-validation score) could be very important for a good model. Therefore it is always important to evaluate the predictive power of a model using a held-out set (or better with cross-validation) prior to computing importances. Permutation importance does not reflect to the intrinsic predictive value of a feature by itself but how important this feature is for a particular model.
The permutation_importance function calculates the feature importance of estimators for a given dataset. The n_repeats parameter sets the number of times a feature is randomly shuffled and returns a sample of feature importances.
Let’s consider the following trained regression model:
Its validation performance, measured via the \(R^2\) score, is significantly larger than the chance level. This makes it possible to use the permutation_importance function to probe which features are most predictive:
Note that the importance values for the top features represent a large fraction of the reference score of 0.356.
Permutation importances can be computed either on the training set or on a held-out testing or validation set. Using a held-out set makes it possible to highlight which features contribute the most to the generalization power of the inspected model. Features that are important on the training set but not on the held-out set might cause the model to overfit.
The permutation feature importance is the decrease in a model score when a single feature value is randomly shuffled. The score function to be used for the computation of importances can be specified with the scoring argument, which also accepts multiple scorers. Using multiple scorers is more computationally efficient than sequentially calling permutation_importance several times with a different scorer, as it reuses model predictions.
The ranking of the features is approximately the same for different metrics even if the scales of the importance values are very different. However, this is not guaranteed and different metrics might lead to significantly different feature importances, in particular for models trained for imbalanced classification problems, for which the choice of the classification metric can be critical.
4.2.1. Outline of the permutation importance algorithm¶
Compute the reference score \(s\) of the model \(m\) on data \(D\) (for instance the accuracy for a classifier or the \(R^2\) for a regressor).
For each feature \(j\) (column of \(D\) ):
Compute importance \(i_j\) for feature \(f_j\) defined as:
4.2.2. Relation to impurity-based importance in trees¶
Tree-based models provide an alternative measure of feature importances based on the mean decrease in impurity (MDI). Impurity is quantified by the splitting criterion of the decision trees (Gini, Entropy or Mean Squared Error). However, this method can give high importance to features that may not be predictive on unseen data when the model is overfitting. Permutation-based feature importance, on the other hand, avoids this issue, since it can be computed on unseen data.
Furthermore, impurity-based feature importance for trees are strongly biased and favor high cardinality features (typically numerical features) over low cardinality features such as binary features or categorical variables with a small number of possible categories.
Permutation-based feature importances do not exhibit such a bias. Additionally, the permutation feature importance may be computed performance metric on the model predictions predictions and can be used to analyze any model class (not just tree-based models).
4.2.3. Misleading values on strongly correlated features¶
When two features are correlated and one of the features is permuted, the model will still have access to the feature through its correlated feature. This will result in a lower importance value for both features, where they might actually be important.
Permutation importance for feature evaluation [BRE].
Parameters estimator object
X ndarray or DataFrame, shape (n_samples, n_features)
Data on which permutation importance will be computed.
y array-like or None, shape (n_samples, ) or (n_samples, n_classes)
Targets for supervised or None for unsupervised.
scoring str, callable, list, tuple, or dict, default=None
Scorer to use. If scoring represents a single score, one can use:
If scoring represents multiple scores, one can use:
a list or tuple of unique strings;
a callable returning a dictionary where the keys are the metric names and the values are the metric scores;
a dictionary with metric names as keys and callables a values.
Passing multiple scores to scoring is more efficient than calling permutation_importance for each of the scores as it reuses predictions to avoid redundant computation.
If None, the estimator’s default scorer is used.
n_repeats int, default=5
Number of times to permute a feature.
n_jobs int or None, default=None
random_state int, RandomState instance, default=None
sample_weight array-like of shape (n_samples,), default=None
Sample weights used in scoring.
New in version 0.24.
The number of samples to draw from X to compute feature importance in each repeat (without replacement).
If int, then draw max_samples samples.
If float, then draw max_samples * X.shape[0] samples.
Dictionary-like object, with the following attributes.
importances_mean ndarray of shape (n_features, )
importances_std ndarray of shape (n_features, )
importances ndarray of shape (n_features, n_repeats)
Интерпретация результатов машинного обучения
Альберт Эйнштейн: «Если вы не можете объяснить что-то простым языком, вы этого не понимаете».
Зачем нужно объяснимое машинное обучение
Модели машинного обучения считаются «черными ящиками». Это не означает, что мы не можем получить от них точный прогноз, мы не можем понятно объяснить или понять логику их работы.
Четкое математическое определение интерпретируемости в машинном обучении отсутствует. Есть несколько определений:
Модель оказывает определенное влияние на последующие принятия решений, например, в системах поддержки принятия врачебных решений (СППВР). Очевидно, что интерпретируемость для СППВР будет гораздо важнее, чем для тех моделей, которые используются для прогнозирования результата классификации вин.
«Проблема заключается в том, что всего одна метрика, такая как точность классификации, является недостаточным описанием большинства реальных задач.» (Доши-Велес и Ким) 2017.
Для понимания и интерпретация работы модели нам потребуются:
Рассмотрим несколько методов, которые помогают извлекать вышеперечисленные особенности из модели.
Permutation Importance
Какие признаки модель считает важными? Какие признаки оказывают наибольшее влияние? Эта концепция называется важностью признаков (feature importance), а Permutation Importance – это метод, широко используемый для вычисления важности признаков. Он помогает нам увидеть, в какой момент модель выдает неожиданные результаты или работает корректно.
Permutation importance отличается:
Допустим, у нас есть датасет. Мы хотим предсказать рост человека в 18 лет, используя данные, которые о нем имеются в 12 лет. Проведя случайное переупорядочивание одного столбца, получим выходные прогнозы менее точными, так как полученные данные больше не соответствуют чему-либо в нашем датасете.
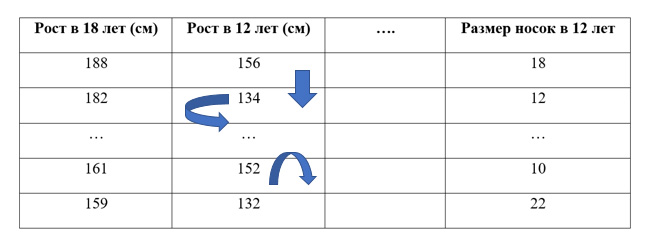
Точность модели особенно страдает, если мы перемешиваем столбец, на который модель сильно опиралась для прогнозов. В этом случае перетасовка «роста в 12 лет» вызвала бы непредсказуемые прогнозы. Если бы вместо этого, мы перетасовали «размер носок», то предсказания не пострадали бы так сильно.
Процесс выявления важности признаков выглядит следующим образом:
Для вычисления permutation importance есть несколько готовых библиотек, рассмотрим примеры работы с ними.
Библиотека SkLearn
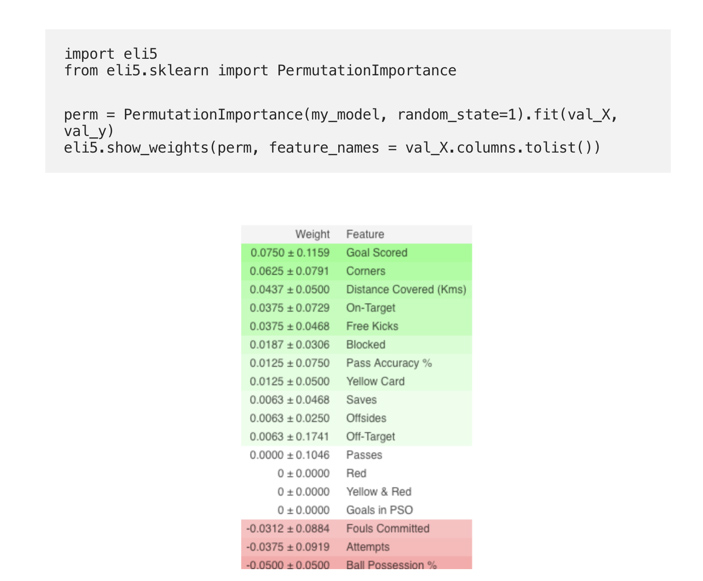
Библиотека ELI5
ELI5 – это библиотека в Python, которая позволяет визуализировать различные модели машинного обучения с помощью унифицированного API (https://github.com/TeamHG-Memex/eli5). Имеет встроенную поддержку для нескольких ML-фреймворков и обеспечивает способы интерпретации модели черного ящика.
Рассмотрим модель, которая предсказывает как играет футбольная команда и сможет ли она пол награду “Man of the Game” или нет, на основе определенных параметров.
(Здесь val_X,val_y обозначают соответственно наборы валидации)
Визуализаторы используются для обнаружения функций или целей, которые могут повлиять на последующую подгонку.
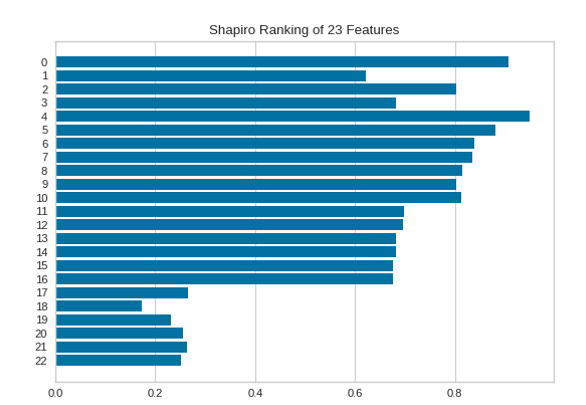
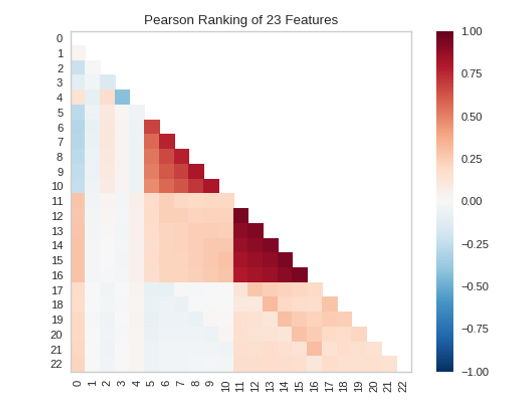
В следующем примере рассматриваются функции Rank1D и Rank2D для оценки отдельных функций и пар функций с помощью различных показателей, которые оценивают функции по шкале [-1, 1] или [0, 1].
При одномерном ранжировании функций [Rank1D] используется алгоритм ранжирования, который учитывает только одну функцию за 1 раз.
Значимость каждого из 23 признаков отображена на следующем рисунке, чем больше значение, тем важнее признак.
При двумерном ранжировании функций [Rank 2D] используется алгоритм ранжирования, который одновременно учитывает пары функций. Для этого удобно использовать корреляцию по Пирсону, которая показывает связь двух признаков между собой. Чем больше число, тем сильнее коррелированы признаки.
Partial Dependence Plots – PDP
График частичной зависимости (PDP или график PD) показывает краевой эффект одного или двух признаков на прогнозируемый результат модели машинного обучения (J. H. Friedman 2001). График частичной зависимости может показать, является ли отношение между целью и признаком линейным, монотонным или более сложным. Например, при применении к модели линейной регрессии графики частичной зависимости всегда показывают линейную зависимость.
Для классификации, где модель машинного обучения выводит вероятности, график частичной зависимости отображает вероятность для определенного класса, заданного различными значениями для признаков. Простым способом для отображения с несколькими классами, является рисование одной линии или графика для каждого класса. График частичной зависимости является глобальным методом: Метод рассматривает все экземпляры и даёт утверждение о глобальной взаимосвязи признака с предсказанным результатом.
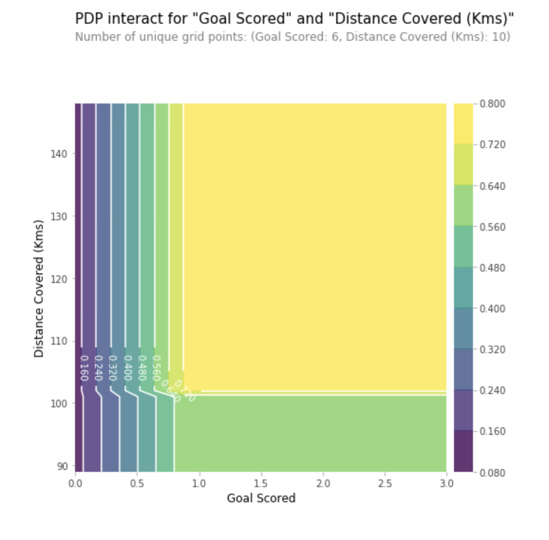
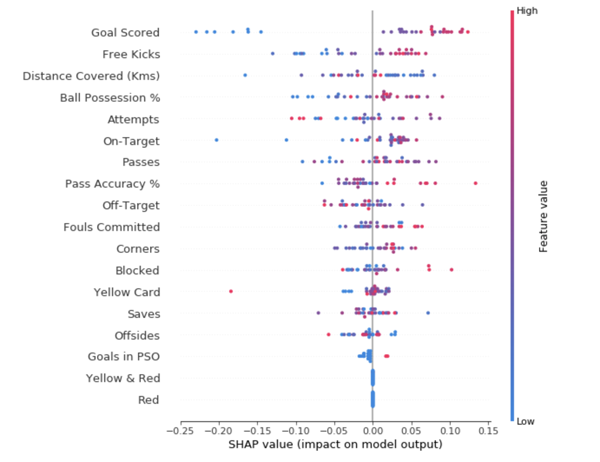
На данном графике Ось Y отражает изменение прогноза вследствие того, что было предсказано в исходном или в крайнем левом значении. Синяя область обозначает интервал доверия. «Goal Scored» мы видим, что забитый гол увеличивает вероятность получения награды ‘Лучший игрок’, но через некоторое время происходит насыщение.
Библиотека SHAP
SHAP – значения показывают, насколько данный конкретный признак изменил предсказание по сравнению при базовом значении этого признака. Допустим, мы хотели узнать, каким был бы прогноз, если бы команда забила 3 гола, вместо фиксированного базового количества.
Признаки, продвигающие прогноз выше, показаны красным цветом, а те, что понижают его точность – ниже.
Агрегирование множества SHAP-значений поможет сформировать более детальное представление о модели. Чтобы получить представление о том, какие признаки наиболее важны для модели, мы можем построить SHAP – значения для каждого признака и для каждой выборки. Сводный график показывает, какие признаки являются наиболее важными, а также их диапазон влияния на датасет.
Для каждой точки цвет показывает, является ли этот объект сильно значимым или слабо значимым для этой строки датасета; Горизонтальное расположение показывает, привело ли влияние значения этого признака к более точному прогнозу или нет.
Значения упорядочены сверху вниз, вверху являются наиболее важными признаками, а значения в направлении к низу имеют наименьшее значение.
Первое число в каждой строке показывает, насколько снизилась производительность модели при случайной перетасовке (в данном случае с использованием «точности» в качестве метрики производительности). Существует некоторая случайность в точном изменении производительности от перетасовки столбца. Мы измеряем количество случайности в нашем вычислении важности перестановки, повторяя процесс с несколькими перестановками. Число после ± измеряет изменение производительности от одной перестановки к следующей. Иногда отображаются отрицательные значения импорта перестановок. В этих случаях прогнозы по перетасованным (или шумным) данным оказались более точными, чем реальные данные. Это происходит, когда функция не имела значения (должна была иметь значение, близкое к 0), но случайный шанс привел к тому, что прогнозы по перетасованным данным были более точными. Это чаще встречается с небольшими наборами данных, как в этом примере, потому что есть больше места для удачи/шанса. Некоторые веса отрицательны. Это связано с тем, что в этих случаях прогнозы по перетасованным данным оказались более точными, чем реальные данные.
Библиотека Yellowbrick
Yellowbrick https://www.scikit-yb.org/en/latest/ предназначена для визуализии признаков и расширяет Scikit-Learn API, чтобы упростить выбор модели и настройку гиперпараметров. Под капотом использует Matplotlib.
Библиотека LIME
Lime поддерживает объяснения для индивидуальных прогнозов широкого круга классификаторов. Встроена поддержка scikit-learn.
Ниже приведен пример одного такого объяснения проблемы классификации текста.
Вывод LIME представляет собой список объяснений, отражающих вклад каждой функции в прогноз выборки данных. Это обеспечивает локальную интерпретируемость, а также позволяет определить, какие изменения характеристик окажут наибольшее влияние на прогноз.
Библиотека MXLtend
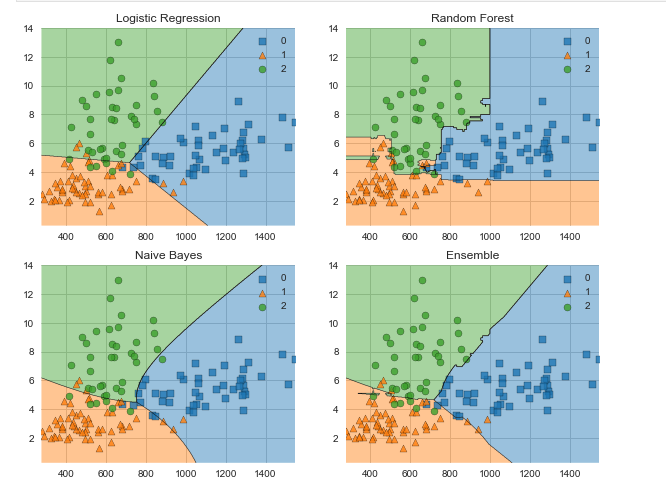
Библиотека MLxtend содержит ряд вспомогательных функций для машинного обучения. Например, для StackingClassifier и VotingClassifier, эволюции модели, извлечения признаков, для разработки и для визуализации данных. С помощью MLxtend и сравним границы решения VotingClassifier и входящих в его состав классификаторов:
Заключение
Интерпретируемость модели важна не меньше, чем качество модели. Для того, чтобы добиться признания, крайне важно, чтобы системы машинного обучения могли предоставить понятные объяснения своих решений. Приведены основные библиотеки под Python для интерпретации модели, которые используют специалисты компании «К-Скай» при создании предиктивных моделей и управления рисками в здравоохранении.