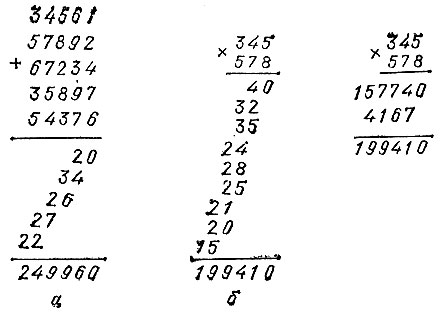три пишем два в уме никольский читать
Три пишем два в уме никольский читать
О книге
Главная редакция физико-математической литературы
доктор физико-математических наук В. Г. Демин
Сергеев И. Н., Олехник С. Н., Гашков С. Б.
С 32 Примени математику.- М.: Наука. Гл. ред. физ.-мат. лит., 1989.- 240 с.
На примере решения большого числа конкретных задач в основном практического содержания показывается, как использовать математические идеи и методы для нахождения выхода из разного рода затруднительных положений, которые могут возникнуть в повседневной жизни. Рассматриваются вопросы построения и измерения ограниченными средствами, поиска оптимального решения в той или иной ситуации, способы быстрого счета, задачи на разрезание, переливание, взвешивание и т. п.
Для школьников и всех любителей математики.
Предисловие
При написании этой книги мы ставили своей целью научить читателя искусству применения математических идей и методов к решению практических и теоретических задач, к нахождению выходов из разного рода затруднительных положений, возникающих в повседневной жизни, и даже к тем вопросам, в которых использование математики поначалу кажется просто невозможным.
Книга представляет собой сборник задач, сгруппированных по темам в отдельные параграфы. В связи с этим принята двойная нумерация задач. Например, задача 14.6 содержится в § 14 и идет там шестой по счету. В начале каждого параграфа приводятся необходимые сведения, соглашения и понятия, используемые в задачах. Решения задач помещены в конце соответствующих параграфов. В пределах одного параграфа задачи расположены в основном по возрастанию трудности. Рекомендуем решать их по порядку и сравнивать полученные решения с приведенными в книге.
Некоторые задачи этого сборника заимствованы из различных занимательных математических книг и журналов. При этом отбирались наиболее интересные и поучительные на наш взгляд задачи, имеющие практическое значение. Многие задачи переработаны нами или придуманы специально для этой книги. Мы старались приводить наиболее простые из известных нам и легко осуществимые на практике решения, доступные по возможности более широкому кругу читателей. Однако вполне допускаем, что какие-то из приведенных решений окажутся не самыми лучшими,
§ 1. Три пишем, два в уме
1.1. Сумма цифр Требуется сложить много однозначных чисел. Как облегчить эту работу и быстрее получить правильный ответ?
Какие приемы позволяют упростить эту работу?
1.3. Необычные записи
На рис. 1 приведены любопытные способы записи операций сложения и умножения многозначных чисел. Разберитесь в этих способах.
1.4. Таблица умножения на пальцах Если вы хорошо знаете таблицу умножения чисел, меньших 5, но почему-то неуверенно себя чувствуете при умножении однозначных чисел, больших 5, то вы можете контролировать себя с помощью пальцев следующим образом. Пусть надо перемножить числа 6 и 7. Загнем на одной руке столько пальцев, на сколько первый сомножитель превышает 5 (в нашем случае 6-5 = 1 палец), а на другой руке столько пальцев, на сколько второй сомножитель превышает 5 (в нашем случае 7-5 = 2 пальца). Если сложить количества загнутых пальцев и перемножить количества незагнутых пальцев, то получится соответственно число десятков 1+2 = 3 и число единиц 4*3 = 12, а сумма 30 + 12 = 42 как раз и будет равна произведению 6*7.
Дайте обоснование предложенному способу умножения;
1.5. Умножение на 9 с помощью пальцев Этот способ настолько прост, что его может освоить любой ребенок, знакомый лишь с элементарным счетом. Пусть нужно умножить 6 на 9. Положив обе руки на стол, приподнимем шестой палец, считая слева направо. Тогда количество пальцев слева от поднятого укажет цифру десятков (в нашем случае
ЛитЛайф
Жанры
Авторы
Книги
Серии
Форум
Сергеев Игорь Николаевич
Книга «Примени математику»
Оглавление
§ 1. Три пишем, два в уме
Решения
Читать
Помогите нам сделать Литлайф лучше
Решения
1.2. Если чисел достаточно много, то среди них с большой вероятностью найдутся пары или тройки чисел, дающие в сумме целое число-десятков. Заменим такие группы чисел их суммами, а затем среди новых слагаемых выделим аналогично группы чисел, дающие в сумме целое число сотен. Действуя таким образом, мы сильно упростим работу по сложению исходных чисел. Например, складывая числа 17, 96, 72, 29, 93, 32, 87, 68, 84, 37, 13, 92, 55, 61, 45, 34, 73, 29, 20, 64, получаем
(17 + 93) + (96 + 84) + (72 + 68) + (29 + 61) + (87 + 13) + (37 + 73) + (55 + 45) + 20 + (32 + 34 + 64) + (92 + 29) = 100 + 180 + 140 + 90 + 100 + 110 + 100 + 20 + 130 + 120 + 1 = (110 + 90) + (180 + 20) + (100 + 100) + (140 + 110 + 130 + 120) + 1 = 200 + 200 + 200 + 500 + 1 = 1101. Попробуйте подсчитать сумму исходных чисел в том порядке, в каком они были записаны вначале, и вы убедитесь, насколько это трудоемкое и нудное занятие.
1.3. Приведенная на рис. 1, а запись есть не что иное, как запись поразрядного сложения многозначных чисел, отличающаяся от обычной тем, что в ней не требуется запоминать никаких цифр при переносе из одного разряда в другой. Так, при сложении цифр единиц всех слагаемых получается 20, что и записано в первой строке под чертой. При сложении цифр десятков всех слагаемых получается 34, что и записано в следующей строке (разумеется, не прямо под предыдущим числом, а со сдвигом на один разряд влево), и т. д.
1.6. Так как 9а = 10а-а, то для умножения числа а на 9 достаточно от увеличенного в 10 раз числа а отнять само число а. Например, при а = 437 имеем
437*9 = 4370-437 = 3933. Аналогично вместо умножения числа а на 99 или на 999 можно умножить его на 100 или на 1000 соответственно, а потом отнять само число а, например,
63 475 = 634*100 + 75 = 634*99 + 634 + 75 = 634*99 + 6*100 + 34 + 75 = 634*99 + 6*99 + 6 + 34 + 75 = 640*99 + 115 = 641*99 + 16, то частное от деления данного числа на 99 равно 641, а остаток 16. Так как
63 475 = 634*98 + 634*2 + 75 = 634*98 + 6*98*2 + 6*2*2 + 34*2 + 75 = 646*98 + 24 + 68 + 75 = 647*98 + 69, то частное от деления на 98 равно 647, а остаток 69. Так как
1.8. Вместо умножения числа а на 5 можно, и это действительно проще, разделить его на 2 и умножить на 10, поскольку 

1275*5 = 637,5*10 = 6375, 1275:5 = 2550:10 = 255. 1.9. Так как 25 = 100 /4, то справедливы формулы 25а = а /4 *100 и а /25 = 4а /100 пользуясь которыми, например, получаем
786*25 = 78 600:4 = 19650, 786:25 = 4*7,86 = 31,44. Что же касается умножения и деления на 125, то здесь аналогично получаем формулы 
786*125 = 786 000:8 = 98 250, 786:125 = 8*0,786 = 6,288. 1.10. Учитывая равенства
(10+а)(10+b) = 100 + 10а + 10b + ab = 10(а+b) + 100 + ab, которые подтверждают правильность предложенного в условии задачи способа.
1.15. Ответ получен из верного равенства
1.16. Пусть нужно перемножить числа 10а+b и 10а+с, удовлетворяющие условию b+с = 10. Тогда имеем
b>(10а+b)(10а+с) = 100а 2 + 10aс + 10bа + bс = 100а 2 + 10а(b+с) + bс = 100а 2 + 100а + bс = 100а(а+1) + bc, что и требовалось доказать.
1.17. Для возведения в квадрат числа, оканчивающегося на 5, достаточно отбросить у него последнюю цифру, а затем перемножить полученное число с числом, большим его на 1, и приписать к результату справа 25. Это правило является следствием равенства, доказанного в решении задачи 1.16, если в нем положить b = с = 5.
1.18. Пусть перемножаются числа 10а+5 и 106+5. Правильность предложенного способа вытекает из следующих равенств:
1.19. Произведение чисел а и b можно найти по формуле
удобной для применения в случае одновременной четности или одновременной нечетности сомножителей (в противном случае их полусумма и полуразность были бы нецелыми) и в случае, когда эти сомножители близки друг к другу.
1.20. Квадраты двух соседних чисел различаются на сумму этих чисел, поскольку имеют место равенства
31 3 = 30 3 + 3*30*31 + 1 = 27 000 + 2790 + 1 = 29 791. 1.22. Вычисление квадратов в разобранных примерах основано на формуле
ЛитЛайф
Жанры
Авторы
Книги
Серии
Форум
Сергеев Игорь Николаевич
Книга «Примени математику»
Оглавление
§ 1. Три пишем, два в уме
Читать
Помогите нам сделать Литлайф лучше
§ 1. Три пишем, два в уме
1.1. Сумма цифр Требуется сложить много однозначных чисел. Как облегчить эту работу и быстрее получить правильный ответ?
Какие приемы позволяют упростить эту работу?
1.3. Необычные записи
На рис. 1 приведены любопытные способы записи операций сложения и умножения многозначных чисел. Разберитесь в этих способах.
1.4. Таблица умножения на пальцах Если вы хорошо знаете таблицу умножения чисел, меньших 5, но почему-то неуверенно себя чувствуете при умножении однозначных чисел, больших 5, то вы можете контролировать себя с помощью пальцев следующим образом. Пусть надо перемножить числа 6 и 7. Загнем на одной руке столько пальцев, на сколько первый сомножитель превышает 5 (в нашем случае 6-5 = 1 палец), а на другой руке столько пальцев, на сколько второй сомножитель превышает 5 (в нашем случае 7-5 = 2 пальца). Если сложить количества загнутых пальцев и перемножить количества незагнутых пальцев, то получится соответственно число десятков 1+2 = 3 и число единиц 4*3 = 12, а сумма 30 + 12 = 42 как раз и будет равна произведению 6*7.
Дайте обоснование предложенному способу умножения;
1.5. Умножение на 9 с помощью пальцев Этот способ настолько прост, что его может освоить любой ребенок, знакомый лишь с элементарным счетом. Пусть нужно умножить 6 на 9. Положив обе руки на стол, приподнимем шестой палец, считая слева направо. Тогда количество пальцев слева от поднятого укажет цифру десятков (в нашем случае 5), а количество пальцев справа от поднятого укажет цифру единиц (равную 4), т, е. искомое произведение будет равно 54.
Объясните, почему предложенный способ дает правильный ответ при умножении любого однозначного числа на 9.
1.6. Вычитание вместо умножения Умножение некоторого числа на 9 можно свести к вычитанию двух чисел. Подумайте, каких. Предложите аналогичный способ умножения чисел на 99, на 999, на числа, близкие к числам 10, 100, 1000 и т. д.
1.7. Быстрое деление Деление числа 63 475 на 999 было произведено следующим образом:
63 475 = 63*1000 + 475 = 63*999 + 63 + 475 = 63*999 + 538, откуда частное равно 63, а остаток 538.
Используя аналогичные преобразования, разделите число 63 475 с остатком на 99, на 98 и на 102.
1.8. Умножение и деление на 5 Трудно не согласиться с тем, что разделить произвольное число на 2 в уме легче, чем умножить его на 5. Нельзя ли воспользоваться этим обстоятельством, чтобы облегчить умножение чисел на 5? Что вы можете предложить вместо деления на 5?
1.9. Умножение и деление на степень пятерки Аналогично умножению или делению на 5 (см. задачу 1.8) можно сравнительно легко в уме умножать или делить числа на 25 и на 125. Как именно?
1.10. С помощью обыкновенных дробей Предложите способы быстрого умножения на 2,5, на 1,25, на 1,5 и на 0,75 (а также на 15 и на 75), использующие представление десятичных дробей в виде обыкновенных.
1.11. Способ удвоения При умножении чисел на степень двойки иногда используется способ, суть которого можно продемонстрировать на следующем примере:
139*32 = 278*16 = 556*8 = 1112*4 = 2224*2 = 4448, Как видоизменить этот способ для умножения на число, близкое к степени, двойки, скажем на 14 или на 35?
1.12. Деление на степень двойки Предложите способ деления чисел на степень двойки, подобный способу удвоения (см. задачу 1.11).
1.13. Умножение чисел второго десятка Для того чтобы перемножить два двузначных числа, меньших 20, достаточно сложить цифры единиц этих чисел и, увеличив сумму в 10 раз, прибавить к ней 100 и произведение тех же цифр.
Дайте обоснование предложенному способу.
1.14. Умножение чисел десятого десятка Для того чтобы перемножить два двузначных числа, близких к 100, достаточно вычесть из одного числа дополнение второго до 100 и, увеличив разность в 100 раз, прибавить к ней произведение дополнений исходных чисел до 100. Например, верны выкладки
93*98 = (93-2)100 + 2*7 = 9114. Дайте обоснование предложенному способу.
1.15. Умножение чисел, близких к 1000 При перемножении чисел 987 и 996 были проделаны вычисления:
987*996 = (987-4)1000 + 4*13 = 983 052. Убедитесь, что в результате найден верный ответ, и объясните способ его получения (сравните с задачей 1.14).
1.16. Устное умножение Докажите, что для перемножения двух чисел, у которых цифры единиц в сумме дают 10, а цифры других разрядов совпадают, достаточно число, получающееся в результате отбрасывания цифры единиц, умножить на следующее за ним натуральное число и, увеличив произведение в 100 раз, прибавить к нему произведение цифр единиц исходных чисел. Например, верны выкладки
62*68 = 6*7*100 + 2*8 = 4216. 1.17. Квадрат числа, оканчивающегося на 5 Сформулируйте общее правило, с помощью которого возведены в квадрат следующие числа:
85 2 = 8*9*100 + 25 = 7225, 115 2 = 11*12*100 + 25= 13225. Откуда вытекает справедливость этого правила?
1.18. Если числа оканчиваются на 5 Докажите, что для перемножения двух чисел, оканчивающихся на 5, достаточно отбросить у каждого числа последнюю цифру, а затем, увеличив большее из полученных чисел на 1, умножить его на меньшее из них и прибавить к результату полуразность тех же чисел, наконец, увеличить ответ в 100 раз и прибавить 25. Например, пользуясь указанным способом, находим произведения
1.19. С помощью квадратов Если вы хорошо помните или умеете быстро восстанавливать в памяти квадраты натуральных чисел, то вы сможете и быстро перемножить, скажем, числа 32 и 36 следующим способом:
1.20. Квадраты близких чисел Пусть вы помните квадрат какого-то числа и хотите по нему быстро восстановить квадрат числа, отличающегося от исходного на 1 или 2. Как это можно сделать, не производя операции возведения в квадрат?
Если вы помните только квадраты чисел, кратных 5, то без особого напряжения сможете восстанавливать квадраты остальных целых чисел. Как именно?
1.21. Следующий куб Пусть вам известен куб некоторого числа. Как с его помощью проще найти куб следующего числа?
1.22. Квадрат числа, близкого к «круглому» Быстрому возведению в квадрат может способствовать умение перемножать в уме любые числа с некоторыми числами специального вида, например
192 2 = 200*184 + 8 2 = 36 864, 412 2 = 400*424 + 12 2 = 169 744. На каком приеме основаны вычисления квадратов в данных примерах?
1.23. Следующие 25 квадратов Если вы знаете квадраты всех чисел от 1 до 25, то вам нет никакой необходимости заучивать квадраты следующих 25 чисел. Для возведения в квадрат любого числа, заключенного между 25 и 50, достаточно отнять от него 25 и, увеличив результат в 100 раз, прибавить к нему квадрат дополнения этого числа до 50. Например, справедливы равенства
37 2 = (37-25)100 + (50-37) 2 = 1200 + 169 = 1369. Дайте обоснование предложенному способу.
1.24. Квадраты чисел, больших 50 Как изменить описанную в задаче 1.23 процедуру возведения в квадрат, чтобы она годилась и для двузначных чисел, больших 50?
1.25. Квадраты чисел, близких к 500 При возведении в квадрат числа 492 были проделаны вычисления
492 2 = (492-250)1000 + (500-492) 2 = 242 064. Убедитесь, что в результате найден верный ответ, и сформулируйте общее правило возведения в квадрат чисел, близких к 500 (сравните с задачами 1.23 и 1.24).
Отец замолчал. Он стоял, по-прежнему повернувшись к окну, я видел только его темную спину, он словно вовсе и не со мной говорил, а просто думал вслух. А может быть, он все-таки ждал, что скажу ему я. Но что я мог сказать. Я молчал.
И снова, будто угадав мои мысли, отец спросил:
— Знаешь, о чем мы говорили сегодня с Галиной Аркадьевной? Может быть, мы не должны, не имеем права публиковать сейчас результаты опытов? Ради памяти Колесова? Только ради его памяти. В конце концов у нас есть еще десятки проблем, которыми мы можем заниматься… и занимаемся…
Я так и не дождался, когда отец ляжет спать. И последнее, что я видел, уже погружаясь в сон, уже чувствуя, как закрываются у меня глаза, была темная фигура отца на фоне окна…
ЧТО Я ТАКОГО СДЕЛАЛ?
И все-таки я придумал. Я решил подарить ей книгу Ремарка «Три товарища». По-моему, это была удачная мысль, мне, во всяком случае, она очень нравилась. Я даже сочинил замысловатую выразительную надпись: «Лиле, от одного из трех». Это было не совсем точно, но
зато красиво. Я имел в виду себя, Эрика и Вадика. Молчаливого Витька и Серегу пришлось не принимать в расчет.
Я старательно отгладил брюки, надел новую рубашку и уже совсем было собрался идти в гости, когда вернулся с работы отец.
Он выпил на кухне чашку бульона, нашего национального кушанья, нашего фирменного блюда, как обычно шутили мы, и прилег на диван. Раньше с ним никогда такого не бывало, он никогда не любил лежать днем.
— Нет, ничего, просто устал немного. Пять часов отсидел на ученом совете.
— Нет, почему же, иди. Иди, конечно.
Я стоял посреди комнаты в нерешительности. В глубине души я чувствовал, что мне лучше не ходить, что я должен остаться с отцом. Но в то же время мне так хотелось пойти! Я ведь собирался весь день, я весь день только и думал об этом, я ведь еще ни разу не был у Лильки дома, в гостях. И потом я же обещал.
Я еще раз посмотрел на отца.
— Пап, ты правда хорошо себя чувствуешь?
— Правда, правда. Иди, а то опоздаешь.
Он оказался прав. Я действительно чуть не опоздал, пришел самым последним, за столом даже не было уже свободного места, пришлось всем потесниться и втиснуть еще один стул. Но зато я оказался рядом с Лилькой, раскрасневшейся, оживленной и веселой.
Я молча пожал плечами: мол, ерунда какая, даже и возражать не стоит.
Сначала за столом все чувствовали себя скованно, не то что во дворе, возле шестой парадной. Хорошо еще хоть Лилькины родичи, выпив по рюмке за новорожденную и выслушав наши вежливые поздравления, удалились не то в другую комнату, не то в кухню и затихли там, словно их и не было вовсе в квартире.
Разговор вяло перебрасывался с одной темы на другую, потом голоса стали звучать громче, веселее, и скоро за столом уже стоял беспорядочный гвалт, все говорили и спорили разом.
— Все великие люди учились плохо. Ты почитай биографии, почитай…
— У «Зенита» никаких шансов…
— По Би-би-си говорили, я же сам слышал…
— Нет, ты ответь, ответь, почему «квас» пишется вместе, а «к вам» отдельно?
— Подумаешь, я однажды три стакана портвейна выпил, и ничего, ни в одном глазу!
— Нет, я лично влюблена в Козакова…
— Девочки, а правда говорят, что Лолита Торрес больше не будет сниматься?
— Ну ты даешь, мотороллер лучше мотоцикла?
Книга Б.Никольский. Три пишем два в уме. 1978 г.
—>
| Доставка: | |
| по городу: | За дополнительную плату: 180.00 р. |
| по стране и миру: | Стоимость доставки по стране 180.00 р По миру 880.00 р |
| Доставка почтой России. Предоплата на карту Сбербанка. Наложенным платежом не отправляю. Оплата покупки 1-3 дня. | |
| Оплата: Банковская карта, PayPal. | |
| Состояние товара: | Б/у. |
| №128955668 |
Подробное описание
| Книга Б.Никольский. Три пишем два в уме. 1978 г. Твёрдый переплёт, 95 страниц. Размер 22 х 14,5 см. Переплёт потерт по краям. Первые два листа надорваны снизу. На страницах немного пятен, чирков карандашом и ручкой. Рисунки Н.Кошелькова. Вопросы по товару и по доставке задавайте до оформления покупки. Просьба не делать необдуманных покупок, так как с продавца автоматически списывается комиссия за сделку. Если сделка не состоялась, то чтобы вернуть эту комиссию, мне придётся оставить негативный отзыв покупателю. Такие правила на сайте Мешок. Обмен и возврат не предусмотрен. Поэтому внимательно смотрите фото и задавайте вопросы до оформления покупки. Оплата покупок на карту банка. ДОСТАВКУ ОПЛАЧИВАЕТ ПОКУПАТЕЛЬ. Цена за доставку указана на странице покупки, ниже описания товара и цены. Эта сумма прибавляется к стоимости товара. Если покупка не оплачена в течение 3-х дней, то сделку отменяю. Если нужно дополнительное время для оплаты, обязательно сообщите. Отправка покупок в течение 3-х дней после полной оплаты лота и пересылки. При покупке нескольких лотов доставка комбинируется. Номер для отслеживания сообщаю покупателю. Также отслеживаю все посылки, сообщаю о прибытии в почтовое отделение покупателя. За работу почты претензии не принимаю ( задержки, потеря, кража, вскрытие, повреждение). Качественную упаковку лотов гарантирую. На встречи с покупателями не езжу. Личных встреч и самовывоза нет. Доставка почтой России. Доставка в Израиль только EMS. Можно отправить СДЭК, но посылки туда забирает и отвозит курьер. Стоимость доставки на Сахалин уточняйте дополнительно, она дороже.
|