уменьшение размерности машинное обучение
Уменьшение размерности
Под уменьшением размерности (англ. dimensionality reduction) в машинном обучении подразумевается уменьшение числа признаков набора данных. Наличие в нем признаков избыточных, неинформативных или слабо информативных может понизить эффективность модели, а после такого преобразования она упрощается, и соответственно уменьшается размер набора данных в памяти и ускоряется работа алгоритмов ML на нем. Уменьшение размерности может быть осуществлено методами выбора признаков (англ. feature selection) или выделения признаков (англ. feature extraction).
Содержание
Выбор признаков [ править ]
Методы выбора признаков оставляют некоторое подмножество исходного набора признаков, избавляясь от признаков избыточных и слабо информативных. Основные преимущества этого класса алгоритмов:
Все методы выбора признаков можно разделить на 5 типов, которые отличаются алгоритмами выбора лишних признаков.
Фильтры [ править ]
Фильтры могут быть:
Преимуществом группы фильтров является простота вычисления релевантности признаков в наборе данных, но недостатком в таком подходе является игнорирование возможных зависимостей между признаками.
Оберточные методы [ править ]
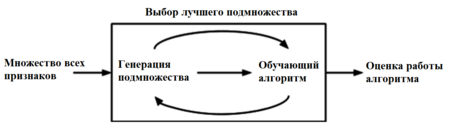
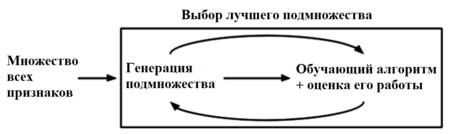
Оберточные методы (англ. wrapper methods) находят подмножество искомых признаков последовательно, используя некоторый классификатор как источник оценки качества выбранных признаков, т.е. этот процесс является циклическим и продолжается до тех пор, пока не будут достигнуты заданные условия останова. Оберточные методы учитывают зависимости между признаками, что является преимуществом по сравнению с фильтрами, к тому же показывают большую точность, но вычисления занимают длительное время, и повышается риск переобучения.
Существует несколько типов оберточных методов: детерминированные, которые изменяют множество признаков по определенному правилу, а также рандомизированные, которые используют генетические алгоритмы для выбора искомого подмножества признаков. Среди детерминированных алгоритмов самыми простыми являются:
Встроенные методы [ править ]
Группа встроенных методов (англ. embedded methods) очень похожа на оберточные методы, но для выбора признаков используется непосредственно структуру некоторого классификатора. В оберточных методах классификатор служит только для оценки работы на данном множестве признаков, тогда как встроенные методы используют какую-то информацию о признаках, которую классификаторы присваивают во время обучения.
Одним из примеров встроенного метода является реализация на случайном лесе: каждому дереву на вход подаются случайное подмножество данных из датасета с каким-то случайным набор признаков, в процессе обучения каждое из деревьев решений производит «голосование» за релевантность его признаков, эти данные агрегируются, и на выходе получаются значения важности каждого признака набора данных. Дальнейший выбор нужных нам признаков уже зависит от выбранного критерия отбора.
Встроенные методы используют преимущества оберточных методов и являются более эффективными, при этом на отбор тратится меньше времени, уменьшается риск переобучения, но т.к. полученный набор признаков был отобран на основе знаний о классификаторе, то есть вероятность, что для другого классификатора это множество признаков уже не будет настолько же релевантным.
Другие методы [ править ]
Есть и другие методы выбора признаков: гибридные (англ. hybrid methods) и ансамблевые (англ. ensemble methods). Гибридные методы комбинируют несколько разных методов выбора признаков, например, некоторое множество фильтров, а потом запускают оберточный или встроенный метод. Таким образом, гибридные методы сочетают в себе преимущества сразу нескольких методов, и на практике повышают эффективность выбора признаков.
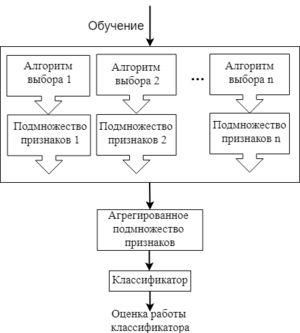
Ансамблевые методы применяются больше для наборов данных с очень большим числом признаков. В данном подходе для начального множества признаков создается несколько подмножеств признаков, и эти группы каким-то образом объединяются, чтобы получить набор самых релевантных признаков. Это довольно гибкая группа методов, т.к. для нее можно применять различные способы выбора признаков и объединения их подмножеств.
Примеры кода scikit-learn [ править ]
Пример кода, реализующего функцию оценки фильтра на основе коэффициента ранговой корреляции:
Пример кода, реализующего SVM-RFE wrapper:
Выделение признаков [ править ]
Другим способом уменьшить размерность входных данных является выделение признаков. Эти методы каким-то образом составляют из уже исходных признаков новые, все также полностью описывающие пространство набора данных, но уменьшая его размерность и теряя в репрезентативности данных, т.к. становится непонятно, за что отвечают новые признаки. Все методы feature extraction можно разделить на линейные и нелинейные.
Одним из самых известных методов линейного выделения признаков является PCA [на 28.01.19 не создан] (Principal Component Analysis, рус. метод главных компонент). Основной идеей этого метода является поиск такой гиперплоскости, на которую при ортогональной проекции всех признаков максимизируется дисперсия. Данное преобразование может быть произведено с помощью сингулярного разложения матриц и создает проекцию только на линейные многомерные плоскости, поэтому и метод находится в категории линейных.
Пример кода scikit-learn [ править ]
Пример выделения признаков с помощью PCA в scikit-learn:
Как уменьшить количество измерений и извлечь из этого пользу

Еще думал написать об автоэнкодерах. В R же, как известно, беда с нейросетевыми библиотеками: либо медленные, либо глючные, либо примитивные. Это и понятно, ведь без полноценной поддержки GPU (и в этом огромный минус R по сравнению с Python) работа со сколь-нибудь сложными нейронными сетями — и в особенности с Deep Learning — практически бессмысленна (хотя есть подающий надежды развивающийся проект MXNet ). Интересен также относительно свежий фреймворк h2o, авторов которого консультирует небезызвестный Trevor Hastie, а Cisco, eBay и PayPal даже используют его для создания своих планов по порабощению человечества. Фреймворк написан на Java (да-да, и очень любит оперативную память). К сожалению, он тоже не поддерживает работу с GPU, т.к. имеет несколько иную целевую аудиторию, но зато отлично масштабируется и предоставляет интерфейс к R и Python (хотя любители мазохизма могут воспользоваться и висящем по дефолту на localhost:54321 web-интерфейсом).
Так вот, если уж возник вопрос о количестве измерений в наборе данных, то это значит, что их, ну, скажем так, довольно много, из-за чего применение алгоритмов машинного обучения становится не совсем удобным. А иногда часть данных — всего лишь информационный шум, бесполезный мусор. Поэтому лишние измерения желательно убрать, вытащив из них по возможности все самое ценное. Кстати, может возникнуть и обратная задача — добавить еще измерений, а попросту — больше интересных и полезных фич. Выделенные компоненты могут быть полезны и для целей визуализации (t-SNE на это, например, и ориентирован). Алгоритмы декомпозиции интересны и сами по себе в качестве машинных методов обучения без учителя, что, согласитесь, иногда может и вовсе привести к решению первичной задачи.
Матричные разложения
В принципе, для сокращения размерности данных с той или иной эффективностью можно приспособить большинство методов машинного обучения — этим, собственно, они и занимаются, отображая одни многомерные пространства в другие. Например, результаты работы PCA и K-means в некотором смысле эквивалентны. Но обычно хочется сокращать размерность данных без особой возни с поиском параметров модели. Самым важным среди таких методов, конечно же, является SVD. «Почему SVD, а не PCA?» — спросите вы. Потому что SVD, во-первых, само по себе является отдельной важной методикой при анализе данных, а полученные в результате разложения матрицы имеют вполне осмысленную интерпретацию с точки зрения машинного обучения; во-вторых, его можно использовать для PCA и с некоторыми оговорками для NMF (как и других методов факторизации матриц); в-третьих, SVD можно приспособить для улучшения результатов работы ICA. Кроме того, у SVD нет таких неудобных свойств, как, например, применимость только к квадратным (разложения LU, Schur) или квадратным симметричным положительно определенным матрицам (Cholesky), или только к матрицам, элементы которых неотрицательны (NMF). Естественно, за универсальность приходится платить — сингулярное разложение довольно медленное; поэтому, когда матрицы слишком большие, применяют рандомизированные алгоритмы.
Что будет, если из исходного изображения вычесть средние значения каждого столбца, разделить полученную матрицу на корень квадратный из количества столбцов в исходной матрице, а потом выполнить сингулярное разложение? Оказывается, что столбцы матрицы V в полученном разложении в точности будут соответствовать главным компонентам, которые получаются при PCA (к слову, в R для PCA можно использовать функцию prcomp() )
Вернемся к вопросу выбора количества главных компонент. Капитанское правило такое: чем больше компонент, тем больше дисперсии они описывают. Andrew Ng, например, советует ориентироваться на >90% дисперсии. Другие исследователи утверждают, что это число может быть и 50%. Даже придуман так называемый параллельный анализ Хорна, который основывается на симуляции Монте-Карло. В R для этого и пакет есть. Совсем простой подход — использовать scree plot: на графике надо искать «локоть» и отбрасывать все компоненты, которые формируют пологую часть этого «локтя». На рисунке ниже, я бы сказал, надо учитывать 6 компонент:
В общем, как вы видите. вопрос неплохо проработан. Также бытует мнение, что PCA применим только для нормально распределенных данных, но Wiki с этим не согласна, и SVD/PCA можно использовать с данными любого распределения, но, конечно, не всегда результативно (что выясняется эмпирически).
Еще одно интересное разложение — это факторизация неотрицательных матриц, которая, как следует из названия, применяется для разложения неотрицательных матриц на неотрицательные матрицы:
X=WH.
В целом, такая задача не имеет точного решения (в отличие от SVD), и для ёё вычисления используют численные алгоритмы. Задачу можно сформулировать в терминах квадратичного программирования — и в этом смысле она будет близка к SVM. В проблеме же сокращения размерности пространства важным является вот что: если матрица Х имеет размерность m x n, то соответственно матрицы W и H имеют размерности m x k и k x n, и, выбирая k намного меньше самих m и n, можно значительно урезать эту самую исходную размерность. NMF любят применят для анализа текстовых данных, там, где неотрицательные матрицы хорошо согласуются с самой природой данных, но в целом спектр применения методики не уступает PCA. Разложение первой картинки в R дает такой результат:
Если требуется что-то более экзотичное
Какое отношение имеет ICA к задаче уменьшения размерности данных? Попробуем представить данные — вне зависимости от их природы — как смесь компонент, тогда можно будет разделить эту смесь на то количество «сигналов», которое нам подходит. Особого критерия, как в случае с PCA, по выбору количества компонент нет — оно подбирается экспериментально.
В самом простом представлении автоэнкодер можно смоделировать как многослойный перцептрон, в котором количество нейронов в выходном слое равно количеству входов. Из рисунка ниже понятно, что, выбирая промежуточный скрытый слой малой размерности, мы тем самым «сжимаем» исходные данные.
Вышеозначенный автоэнкодер несложно превратить в denoising autoencoder. Так как такому автокодировщику на вход надо подавать искаженные образы, перед первым скрытым слоем достаточно разместить dropout слой. Благодаря ему с некоторой вероятностью нейроны будут находиться в «выключенном» состоянии, что а) будет вносить искажения в обрабатываемый образ; б) будет служить своеобразной регуляризацией при обучении.
Еще одно интересное применение автоэнкодера — определение аномалий в данных по ошибке реконструкции образов. В целом, если подавать на вход автоэнкодера данные не из обучающей выборки, то, понятно, ошибка реконструкции каждого образа из новой выборки будет выше таковой из тренировочной выборки, но более-менее одного порядка. При наличии аномалий эта ошибка будет в десятки, а то и сотни раз больше.
Руководство для начинающих по уменьшению размерности в машинном обучении
Дата публикации Mar 11, 2019
Это моя первая статья в среде. Здесь я кратко расскажу о том, что такое уменьшение размерности, зачем оно нам и как это сделать.
Что такое уменьшение размерности?
Это все хорошо, но почему мы должны заботиться? Зачем нам отбрасывать 80 столбцов из нашего набора данных, если мы можем напрямую передать его в наш алгоритм машинного обучения и позволить ему делать все остальное?
Проклятие размерности
Мы заботимся, потому что проклятие размерности требует того, что мы делаем. Проклятие размерности относится ко всем проблемам, возникающим при работе с данными в более высоких измерениях, которых не было в более низких измерениях.
По мере увеличения числа признаков, количество образцов также увеличивается пропорционально. Чем больше функций у нас есть, тем большее количество выборок нам потребуется, чтобы все комбинации значений признаков были хорошо представлены в нашей выборке.
По мере увеличения количества функций модель становится все более сложной. Чем больше функций, тем больше шансов на переоснащение. Модель машинного обучения, которая обучается по большому количеству функций, становится все более зависимой от данных, на которых она обучалась, и, в свою очередь, переоснащается, что приводит к снижению производительности реальных данных, превосходя цель.
Избегание переоснащения является основной мотивацией для уменьшения размерности. Чем меньше возможностей в наших данных обучения, тем меньше допущений делает наша модель и тем проще она будет. Но это еще не все, и уменьшение размерности может предложить гораздо больше преимуществ, таких как
Выбор функций и разработка функций для уменьшения размерности
Уменьшение размерности может быть сделано как методами выбора признаков, так и методами проектирования элементов.
Выбор функции может быть сделан вручную или программно. Например, представьте, что вы пытаетесь построить модель, которая предсказывает вес людей, и вы собрали большой массив данных, который достаточно подробно описывает каждого человека. Если бы у вас была колонка, в которой описывался цвет одежды каждого человека, это сильно помогло бы предсказать его вес? Я думаю, что мы можем с уверенностью согласиться, что этого не произойдет. Это то, что мы можем оставить без дальнейших церемоний. А как насчет столбца, который описал их высоты? Это определенно да. Мы можем сделать эти простые ручные функции выбора и уменьшить размерность, когда актуальность или нерелевантность определенных функций очевидна или общеизвестна. И когда это неочевидно очевидно, есть много инструментов, которые мы могли бы использовать, чтобы помочь нашему выбору функций.
Теперь давайте рассмотрим несколько программных методов для выбора функций из популярного научного комплекта библиотеки машинного обучения, а именно:
Univariate Feature Selection использует статистические тесты для выбора функций. Univariate описывает тип данных, который состоит из наблюдений только по одному признаку или атрибуту. При выборе одномерного объекта каждый объект рассматривается отдельно, чтобы определить степень связи объекта с переменной отклика. Некоторыми примерами статистических тестов, которые можно использовать для оценки релевантности признаков, являются корреляция Пирсона, максимальный информационный коэффициент, корреляция расстояний, ANOVA и хи-квадрат Хи-квадрат используется, чтобы найти связь между категориальными переменными, и Anova предпочтительна, когда переменные непрерывны.
Выбор характеристик является самым простым методом уменьшения размерности. Мы рассмотрим несколько методов проектирования функций для уменьшения размерности позже.
Методы уменьшения линейной размерности
Наиболее распространенными и хорошо известными методами уменьшения размерности являются те, которые применяют линейные преобразования, такие как
Нелинейные методы уменьшения размерности
Методы нелинейного преобразования или методы обучения многообразия используются, когда данные не лежат в линейном подпространстве. Он основан на гипотезе о многообразии, которая гласит, что в многомерной структуре наиболее релевантная информация сосредоточена в небольшом количестве низкоразмерных многообразий. Если линейное подпространство представляет собой плоский лист бумаги, то свернутый лист бумаги является простым примером нелинейного многообразия. Неформально это называется швейцарским креном, канонической задачей в области нелинейного уменьшения размерности. Некоторые популярные методы обучения
Авто-кодеры
Другим популярным методом уменьшения размерности, который дает впечатляющие результаты, являются авто-кодеры, тип искусственной нейронной сети, которая стремится копировать свои входные данные в свои выходные. Они сжимают вход впредставление в скрытом пространстве, а затем восстанавливает вывод из этого представления. Автоэнкодер состоит из двух частей:
В последующих статьях давайте более подробно рассмотрим линейные и нелинейные методы уменьшения размерности.
Уменьшение размерности в Python с помощью Scikit-Learn
Уменьшение размерности выбирает наиболее важные компоненты пространства признаков, сохраняя их, чтобы бороться с переоснащением. В этой статье мы уменьшим размеры нескольких наборов данных, используя широкий спектр методов в Python с помощью Scikit-Learn.
Вступление
В машинном обучении производительность модели только выигрывает от большего количества функций до определенного момента. Чем больше объектов вводится в модель, тем больше увеличивается размерность данных. По мере увеличения размерности становится все более вероятным переоснащение.
Зачем Нужно Уменьшение Размерности?
Существует несколько причин, по которым уменьшение размерности используется в машинном обучении: для борьбы с вычислительными затратами, для контроля переоснащения, а также для визуализации и интерпретации многомерных наборов данных.
Часто в машинном обучении, чем больше функций присутствует в наборе данных, тем лучше классификатор может учиться. Однако большее количество функций также означает более высокие вычислительные затраты. Мало того, что высокая размерность может привести к длительному времени обучения, большее количество функций часто приводит к переоснащению алгоритма, когда он пытается создать модель, объясняющую все функции в данных.
Поскольку уменьшение размерности уменьшает общее количество функций, это может уменьшить вычислительные требования, связанные с обучением модели, но также помогает бороться с переобучением, сохраняя функции, которые будут подаваться в модель, достаточно простыми.
Основными алгоритмами, используемыми для уменьшения размерности при неконтролируемом обучении, являются Анализ главных компонент (PCA) и Сингулярная декомпозиция (SVD).
В случае контролируемого обучения уменьшение размерности может быть использовано для упрощения функций, подаваемых в классификатор машинного обучения. Наиболее распространенными методами, используемыми для уменьшения размерности задач контролируемого обучения, являются линейный дискриминантный анализ (LDA) и PCA, и они могут быть использованы для прогнозирования новых случаев.
Обратите внимание, что случаи использования, описанные выше, являются общими случаями использования, а не единственными условиями, в которых используются эти методы. В конце концов, методы уменьшения размерности являются статистическими методами, и их использование не ограничивается моделями машинного обучения.
Давайте уделим некоторое время объяснению идей, лежащих в основе каждого из наиболее распространенных методов уменьшения размерности.
Анализ основных компонентов
Анализ главных компонент (PCA) – это статистический метод, который создает новые объекты или характеристики данных путем анализа характеристик набора данных. По существу, характеристики данных суммируются или объединяются вместе. Вы также можете представить себе анализ главных компонент как “сдавливание” данных всего в несколько измерений из пространства гораздо более высоких измерений.
Чтобы быть более конкретным, напиток может быть описан многими признаками, но многие из этих признаков будут избыточными и относительно бесполезными для идентификации рассматриваемого напитка. Вместо того, чтобы описывать вино с такими характеристиками, как аэрация, уровень С02 и т. Д., их легче было бы описать цветом, вкусом и возрастом.
Анализ основных компонентов выбирает “основные” или наиболее влиятельные характеристики набора данных и создает на их основе объекты. При выборе только тех объектов, которые оказывают наибольшее влияние на набор данных, размерность уменьшается.
Предполагается, что новые компоненты ортогональны или не связаны друг с другом.
Пример реализации PCA
Теперь мы будем масштабировать объекты с помощью стандартного скаляра. Это необязательно, так как на самом деле мы не запускаем классификатор, но это может повлиять на то, как наши данные анализируются PCA:
Теперь мы будем использовать PCA, чтобы получить список функций и построить график, какие функции имеют наибольшую объяснительную силу или имеют наибольшую дисперсию. Это основные компоненты. Похоже, что около 17 или 18 функций объясняют большинство, почти 95% наших данных:
Давайте преобразуем эти функции в 17 лучших функций. Затем мы построим точечную диаграмму классификации точек данных на основе этих 17 признаков:
Давайте также сделаем это для топ-2 признаков и посмотрим, как изменится классификация:
Сингулярная декомпозиция
Цель сингулярной декомпозиции состоит в том, чтобы упростить матрицу и облегчить выполнение вычислений с ней. Матрица сводится к ее составным частям, подобным цели СПС. Понимание всех тонкостей SVD не является полностью необходимым для реализации его в ваших моделях машинного обучения, но наличие интуиции относительно того, как он работает, даст вам лучшее представление о том, когда его использовать.
SVD может выполняться как на комплексных, так и на вещественных матрицах, но чтобы сделать это объяснение более понятным, мы рассмотрим метод разложения вещественной матрицы.
При выполнении SVD у нас есть матрица, заполненная данными, и мы хотим уменьшить количество столбцов в матрице. Это уменьшает размерность матрицы, сохраняя при этом как можно большую вариабельность данных.
Можно сказать, что матрица A равна транспозиции матрицы V:
Пример реализации SVD
Одним из наиболее распространенных способов использования SVD является сжатие изображений. В конце концов, значения пикселей, которые составляют красный, зеленый и синий каналы в изображении, могут быть просто уменьшены, и в результате получится изображение, которое является менее сложным, но все еще содержит то же самое содержание изображения. Давайте попробуем использовать SVD для сжатия изображения и его рендеринга.
Сначала мы просто напишем функцию для загрузки изображения и превратим ее в массив Numpy. Затем мы хотим выбрать красный, зеленый и синий цветовые каналы из изображения:
Теперь, когда у нас есть цвета, нам нужно сжать цветовые каналы. Мы можем начать с вызова функции SVD Numpy на нужном нам цветовом канале. Затем мы создадим массив нулей, который будем заполнять после завершения умножения матрицы. Затем мы указываем предел сингулярного значения, который мы хотим использовать при выполнении вычислений:
После этого мы делаем матричное умножение по диагонали и пределы значений в U-матрице, как описано выше. Это дает нам левую матрицу, а затем мы умножаем ее на V-матрицу. Это должно привести нас к сжатым значениям, которые мы преобразуем в тип ‘uint8’:
Мы будем использовать это изображение собаки, чтобы проверить наше сжатие SVD на:
Нам также нужно установить предел сингулярного значения, который мы будем использовать, давайте пока начнем с 600:
Наконец, мы можем получить сжатые значения для трех цветовых каналов и преобразовать их из массивов Numpy в компоненты изображения с помощью PIL. Затем мы просто должны соединить три канала вместе и показать изображение. Это изображение должно быть немного меньше и проще, чем исходное изображение:
Действительно, если вы посмотрите на размер изображений, вы заметите, что сжатые изображения меньше, хотя у нас также было немного сжатия с потерями. Вы также можете увидеть некоторый шум на изображении.
Вы можете поиграть с регулировкой предела сингулярного значения. Чем ниже выбранный предел, тем больше будет сжатие, но в определенный момент появится искусственное изображение, и качество изображения ухудшится:
Линейный дискриминантный анализ
Линейный дискриминантный анализ работает путем проецирования данных из многомерного графа на линейный граф. Проще всего представить себе это с помощью графика, заполненного точками данных двух различных классов. Предполагая, что нет линии, которая аккуратно разделит данные на два класса, двумерный граф можно свести к 1D-графу. Затем этот 1D-график можно использовать для достижения наилучшего разделения точек данных.
Когда LDA выполняется, есть две основные цели: минимизация дисперсии двух классов и максимизация расстояния между средними значениями двух классов данных.
Для этого на двумерном графике будет построена новая ось. Эта новая ось должна разделять две точки данных на основе ранее упомянутых критериев. После создания новой оси точки данных в 2D-графике перерисовываются вдоль новой оси.
LDA выполняет три различных шага для перемещения исходного графика на новую ось. Во-первых, должна быть рассчитана разделимость между классами, и это основано на расстоянии между средними классами или дисперсии между классами. На следующем этапе необходимо вычислить дисперсию внутри класса, которая представляет собой расстояние между средним значением и выборкой для различных классов. Наконец, должно быть построено пространство более низкой размерности, которое максимизирует дисперсию между классами.
LDA работает лучше всего, когда средства классов находятся далеко друг от друга. Если средства распределения будут общими, то LDA не сможет разделить классы с помощью новой линейной оси.
Пример реализации LDA
Наконец, давайте посмотрим, как LDA можно использовать для уменьшения размерности. Заметим, что LDA может быть использован в качестве алгоритма классификации в дополнение к проведению редукции размерности.
Давайте начнем с того, что сделаем весь наш необходимый импорт:
Теперь мы загрузим наши обучающие данные, которые разделим на обучающие и проверочные наборы.
Нам нужно масштабировать значения, но инструмент Scaler принимает массивы, поэтому значения, которые мы хотим изменить, сначала должны быть превращены в массивы. После этого мы можем масштабировать данные:
Теперь мы можем выбрать обучающие функции и метки и использовать train_test_split для создания наших обучающих и проверочных данных. Классификацию с помощью LDA сделать легко, вы справляетесь с ней точно так же, как с любым другим классификатором в Scikit-Learn.
Просто установите функцию на обучающие данные и попросите ее предсказать результаты валидации/тестирования. Затем мы можем напечатать метрики для прогнозов относительно фактических значений:
Когда дело доходит до преобразования данных и уменьшения размерности, давайте сначала запустим классификатор логистической регрессии на данных, чтобы мы могли увидеть, какова наша производительность до уменьшения размерности:
Теперь мы преобразуем объекты данных, указав ряд необходимых компонентов для LDA и установив модель на объекты и метки. Затем мы просто преобразуем объекты и сохраняем их в новую переменную. Давайте распечатаем исходное и уменьшенное количество функций:
Вот распечатка для приведенного выше кода:
Теперь нам просто нужно снова сделать разделение train/test с новыми функциями и снова запустить классификатор, чтобы увидеть, как изменилась производительность:
Вывод
Мы рассмотрели основные методы сокращения размерности: Анализ главных компонент, Сингулярное разложение и Линейный дискриминантный анализ. Это статистические методы, которые вы можете использовать, чтобы помочь вашим моделям машинного обучения работать лучше, бороться с переобучением и помогать в анализе данных.
Хотя эти три метода являются наиболее часто используемыми методами уменьшения размерности, существуют и другие. Другие методы размерности включают аппроксимацию ядра и isomap спектральное вложение.