восстановление регрессии машинное обучение
5 алгоритмов регрессии в машинном обучении, о которых вам следует знать

Источник: Vecteezy
Да, линейная регрессия не единственная
Быстренько назовите пять алгоритмов машинного обучения.
Вряд ли вы назовете много алгоритмов регрессии. В конце концов, единственным широко распространенным алгоритмом регрессии является линейная регрессия, главным образом из-за ее простоты. Однако линейная регрессия часто неприменима к реальным данным из-за слишком ограниченных возможностей и ограниченной свободы маневра. Ее часто используют только в качестве базовой модели для оценки и сравнения с новыми подходами в исследованиях.
Команда Mail.ru Cloud Solutions перевела статью, автор которой описывает 5 алгоритмов регрессии. Их стоит иметь в своем наборе инструментов наряду с популярными алгоритмами классификации, такими как SVM, дерево решений и нейронные сети.
1. Нейросетевая регрессия
Теория
Нейронные сети невероятно мощные, но их обычно используют для классификации. Сигналы проходят через слои нейронов и обобщаются в один из нескольких классов. Однако их можно очень быстро адаптировать в регрессионные модели, если изменить последнюю функцию активации.
Каждый нейрон передает значения из предыдущей связи через функцию активации, служащую цели обобщения и нелинейности. Обычно активационная функция — это что-то вроде сигмоиды или функции ReLU (выпрямленный линейный блок).

Источник. Свободное изображение
Но, заменив последнюю функцию активации (выходной нейрон) линейной функцией активации, выходной сигнал можно отобразить на множество значений, выходящих за пределы фиксированных классов. Таким образом, на выходе будет не вероятность отнесения входного сигнала к какому-либо одному классу, а непрерывное значение, на котором фиксирует свои наблюдения нейронная сеть. В этом смысле можно сказать, что нейронная сеть как бы дополняет линейную регрессию.
Нейросетевая регрессия имеет преимущество нелинейности (в дополнение к сложности), которую можно ввести с сигмоидной и другими нелинейными функциями активации ранее в нейронной сети. Однако чрезмерное использование ReLU в качестве функции активации может означать, что модель имеет тенденцию избегать вывода отрицательных значений, поскольку ReLU игнорирует относительные различия между отрицательными значениями.
Это можно решить либо ограничением использования ReLU и добавлением большего количества отрицательных значений соответствующих функций активации, либо нормализацией данных до строго положительного диапазона перед обучением.
Реализация
Используя Keras, построим структуру искусственной нейронной сети, хотя то же самое можно было бы сделать со сверточной нейронной сетью или другой сетью, если последний слой является либо плотным слоем с линейной активацией, либо просто слоем с линейной активацией. (Обратите внимание, что импорты Keras не указаны для экономии места).
model = Sequential()
model.add(Dense(100, input_dim=3, activation=’sigmoid’))
model.add(ReLU(alpha=1.0))
model.add(Dense(50, activation=’sigmoid’))
model.add(ReLU(alpha=1.0))
model.add(Dense(25, activation=’softmax’))
#IMPORTANT PART
model.add(Dense(1, activation=’linear’))
Проблема нейронных сетей всегда заключалась в их высокой дисперсии и склонности к переобучению. В приведенном выше примере кода много источников нелинейности, таких как SoftMax или sigmoid.
Если ваша нейронная сеть хорошо справляется с обучающими данными с чисто линейной структурой, возможно, лучше использовать регрессию с усеченным деревом решений, которая эмулирует линейную и высокодисперсную нейронную сеть, но позволяет дата-сайентисту лучше контролировать глубину, ширину и другие атрибуты для контроля переобучения.
2. Регрессия дерева решений
Теория
Деревья решений в классификации и регрессии очень похожи, поскольку работают путем построения деревьев с узлами «да/нет». Однако в то время как конечные узлы классификации приводят к одному значению класса (например, 1 или 0 для задачи бинарной классификации), деревья регрессии заканчиваются значением в непрерывном режиме (например, 4593,49 или 10,98).

Иллюстрация автора
Из-за специфической и высокодисперсной природы регрессии просто как задачи машинного обучения, регрессоры дерева решений следует тщательно обрезать. Тем не менее, подход к регрессии нерегулярен — вместо того, чтобы вычислять значение в непрерывном масштабе, он приходит к заданным конечным узлам. Если регрессор обрезан слишком сильно, у него слишком мало конечных узлов, чтобы должным образом выполнить свою задачу.
Следовательно, дерево решений должно быть обрезано так, чтобы оно имело наибольшую свободу (возможные выходные значения регрессии — количество конечных узлов), но недостаточно, чтобы оно было слишком глубоким. Если его не обрезать, то и без того высокодисперсный алгоритм станет чрезмерно сложным из-за природы регрессии.
Реализация
Регрессия дерева решений может быть легко создана в sklearn :
Бонус: близкий родственник дерева решений, алгоритм random forest (алгоритм случайного леса), также может быть реализован в качестве регрессора. Регрессор случайного леса может работать лучше или не лучше, чем дерево решений в регрессии (в то время как он обычно работает лучше в классификации) из-за тонкого баланса между избыточным и недостаточным в природе алгоритмов построения дерева.
3. Регрессия LASSO
Метод регрессии лассо (LASSO, Least Absolute Shrinkage and Selection Operator) — это вариация линейной регрессии, специально адаптированная для данных, которые демонстрируют сильную мультиколлинеарность (то есть сильную корреляцию признаков друг с другом).
Она автоматизирует части выбора модели, такие как выбор переменных или исключение параметров. LASSO использует сжатие коэффициентов (shrinkage), то есть процесс, в котором значения данных приближаются к центральной точке (например среднему значению).

Иллюстрация автора. Упрощенная визуализация процесса сжатия
Процесс сжатия добавляет регрессионным моделям несколько преимуществ:
Регрессия лассо использует регуляризацию L1, то есть взвешивает ошибки по их абсолютному значению. Вместо, например, регуляризации L2, которая взвешивает ошибки по их квадрату, чтобы сильнее наказывать за более значительные ошибки.
Такая регуляризация часто приводит к более разреженным моделям с меньшим количеством коэффициентов, так как некоторые коэффициенты могут стать нулевыми и, следовательно, будут исключены из модели. Это позволяет ее интерпретировать.
Реализация
В sklearn регрессия лассо поставляется с моделью перекрестной проверки, которая выбирает наиболее эффективные из многих обученных моделей с различными фундаментальными параметрами и путями обучения, что автоматизирует задачу, которую иначе пришлось бы выполнять вручную.
4. Гребневая регрессия (ридж-регрессия)
Теория
Гребневая регрессия или ридж-регрессия очень похожа на регрессию LASSO в том, что она применяет сжатие. Оба алгоритма хорошо подходят для наборов данных с большим количеством признаков, которые не являются независимыми друг от друга (коллинеарность).
Однако самое большое различие между ними в том, что гребневая регрессия использует регуляризацию L2, то есть ни один из коэффициентов не становится нулевым, как это происходит в регрессии LASSO. Вместо этого коэффициенты всё больше приближаются к нулю, но не имеют большого стимула достичь его из-за природы регуляризации L2.

Сравнение ошибок в регрессии лассо (слева) и гребневой регрессии (справа). Поскольку гребневая регрессия использует регуляризацию L2, ее площадь напоминает круг, тогда как регуляризация лассо L1 рисует прямые линии. Свободное изображение. Источник
В лассо улучшение от ошибки 5 до ошибки 4 взвешивается так же, как улучшение от 4 до 3, а также от 3 до 2, от 2 до 1 и от 1 до 0. Следовательно, больше коэффициентов достигает нуля и устраняется больше признаков.
Однако в гребневой регрессии улучшение от ошибки 5 до ошибки 4 вычисляется как 5² − 4² = 9, тогда как улучшение от 4 до 3 взвешивается только как 7. Постепенно вознаграждение за улучшение уменьшается; следовательно, устраняется меньше признаков.
Гребневая регрессия лучше подходит в ситуации, когда мы хотим сделать приоритетными большое количество переменных, каждая из которых имеет небольшой эффект. Если в модели требуется учитывать несколько переменных, каждая из которых имеет средний или большой эффект, лучшим выбором будет лассо.
Реализация
Гребневую регрессию в sklearn можно реализовать следующим образом (см. ниже). Как и для регрессии лассо, в sklearn есть реализация для перекрестной проверки выбора лучших из многих обученных моделей.
5. Регрессия ElasticNet
Теория
ElasticNet стремится объединить лучшее из гребневой регрессии и регрессии лассо, комбинируя регуляризацию L1 и L2.
Лассо и гребневая регрессия представляют собой два различных метода регуляризации. В обоих случаях λ — это ключевой фактор, который контролирует размер штрафа:
5 алгоритмов регрессии в машинном обучении, о которых вам следует знать

Источник: Vecteezy
Да, линейная регрессия не единственная
Быстренько назовите пять алгоритмов машинного обучения.
Вряд ли вы назовете много алгоритмов регрессии. В конце концов, единственным широко распространенным алгоритмом регрессии является линейная регрессия, главным образом из-за ее простоты. Однако линейная регрессия часто неприменима к реальным данным из-за слишком ограниченных возможностей и ограниченной свободы маневра. Ее часто используют только в качестве базовой модели для оценки и сравнения с новыми подходами в исследованиях.
Команда Mail.ru Cloud Solutions перевела статью, автор которой описывает 5 алгоритмов регрессии. Их стоит иметь в своем наборе инструментов наряду с популярными алгоритмами классификации, такими как SVM, дерево решений и нейронные сети.
1. Нейросетевая регрессия
Теория
Нейронные сети невероятно мощные, но их обычно используют для классификации. Сигналы проходят через слои нейронов и обобщаются в один из нескольких классов. Однако их можно очень быстро адаптировать в регрессионные модели, если изменить последнюю функцию активации.
Каждый нейрон передает значения из предыдущей связи через функцию активации, служащую цели обобщения и нелинейности. Обычно активационная функция — это что-то вроде сигмоиды или функции ReLU (выпрямленный линейный блок).

Источник. Свободное изображение
Но, заменив последнюю функцию активации (выходной нейрон) линейной функцией активации, выходной сигнал можно отобразить на множество значений, выходящих за пределы фиксированных классов. Таким образом, на выходе будет не вероятность отнесения входного сигнала к какому-либо одному классу, а непрерывное значение, на котором фиксирует свои наблюдения нейронная сеть. В этом смысле можно сказать, что нейронная сеть как бы дополняет линейную регрессию.
Нейросетевая регрессия имеет преимущество нелинейности (в дополнение к сложности), которую можно ввести с сигмоидной и другими нелинейными функциями активации ранее в нейронной сети. Однако чрезмерное использование ReLU в качестве функции активации может означать, что модель имеет тенденцию избегать вывода отрицательных значений, поскольку ReLU игнорирует относительные различия между отрицательными значениями.
Это можно решить либо ограничением использования ReLU и добавлением большего количества отрицательных значений соответствующих функций активации, либо нормализацией данных до строго положительного диапазона перед обучением.
Реализация
Используя Keras, построим структуру искусственной нейронной сети, хотя то же самое можно было бы сделать со сверточной нейронной сетью или другой сетью, если последний слой является либо плотным слоем с линейной активацией, либо просто слоем с линейной активацией. (Обратите внимание, что импорты Keras не указаны для экономии места).
model = Sequential()
model.add(Dense(100, input_dim=3, activation=’sigmoid’))
model.add(ReLU(alpha=1.0))
model.add(Dense(50, activation=’sigmoid’))
model.add(ReLU(alpha=1.0))
model.add(Dense(25, activation=’softmax’))
#IMPORTANT PART
model.add(Dense(1, activation=’linear’))
Проблема нейронных сетей всегда заключалась в их высокой дисперсии и склонности к переобучению. В приведенном выше примере кода много источников нелинейности, таких как SoftMax или sigmoid.
Если ваша нейронная сеть хорошо справляется с обучающими данными с чисто линейной структурой, возможно, лучше использовать регрессию с усеченным деревом решений, которая эмулирует линейную и высокодисперсную нейронную сеть, но позволяет дата-сайентисту лучше контролировать глубину, ширину и другие атрибуты для контроля переобучения.
2. Регрессия дерева решений
Теория
Деревья решений в классификации и регрессии очень похожи, поскольку работают путем построения деревьев с узлами «да/нет». Однако в то время как конечные узлы классификации приводят к одному значению класса (например, 1 или 0 для задачи бинарной классификации), деревья регрессии заканчиваются значением в непрерывном режиме (например, 4593,49 или 10,98).

Иллюстрация автора
Из-за специфической и высокодисперсной природы регрессии просто как задачи машинного обучения, регрессоры дерева решений следует тщательно обрезать. Тем не менее, подход к регрессии нерегулярен — вместо того, чтобы вычислять значение в непрерывном масштабе, он приходит к заданным конечным узлам. Если регрессор обрезан слишком сильно, у него слишком мало конечных узлов, чтобы должным образом выполнить свою задачу.
Следовательно, дерево решений должно быть обрезано так, чтобы оно имело наибольшую свободу (возможные выходные значения регрессии — количество конечных узлов), но недостаточно, чтобы оно было слишком глубоким. Если его не обрезать, то и без того высокодисперсный алгоритм станет чрезмерно сложным из-за природы регрессии.
Реализация
Регрессия дерева решений может быть легко создана в sklearn :
Бонус: близкий родственник дерева решений, алгоритм random forest (алгоритм случайного леса), также может быть реализован в качестве регрессора. Регрессор случайного леса может работать лучше или не лучше, чем дерево решений в регрессии (в то время как он обычно работает лучше в классификации) из-за тонкого баланса между избыточным и недостаточным в природе алгоритмов построения дерева.
3. Регрессия LASSO
Метод регрессии лассо (LASSO, Least Absolute Shrinkage and Selection Operator) — это вариация линейной регрессии, специально адаптированная для данных, которые демонстрируют сильную мультиколлинеарность (то есть сильную корреляцию признаков друг с другом).
Она автоматизирует части выбора модели, такие как выбор переменных или исключение параметров. LASSO использует сжатие коэффициентов (shrinkage), то есть процесс, в котором значения данных приближаются к центральной точке (например среднему значению).

Иллюстрация автора. Упрощенная визуализация процесса сжатия
Процесс сжатия добавляет регрессионным моделям несколько преимуществ:
Регрессия лассо использует регуляризацию L1, то есть взвешивает ошибки по их абсолютному значению. Вместо, например, регуляризации L2, которая взвешивает ошибки по их квадрату, чтобы сильнее наказывать за более значительные ошибки.
Такая регуляризация часто приводит к более разреженным моделям с меньшим количеством коэффициентов, так как некоторые коэффициенты могут стать нулевыми и, следовательно, будут исключены из модели. Это позволяет ее интерпретировать.
Реализация
В sklearn регрессия лассо поставляется с моделью перекрестной проверки, которая выбирает наиболее эффективные из многих обученных моделей с различными фундаментальными параметрами и путями обучения, что автоматизирует задачу, которую иначе пришлось бы выполнять вручную.
4. Гребневая регрессия (ридж-регрессия)
Теория
Гребневая регрессия или ридж-регрессия очень похожа на регрессию LASSO в том, что она применяет сжатие. Оба алгоритма хорошо подходят для наборов данных с большим количеством признаков, которые не являются независимыми друг от друга (коллинеарность).
Однако самое большое различие между ними в том, что гребневая регрессия использует регуляризацию L2, то есть ни один из коэффициентов не становится нулевым, как это происходит в регрессии LASSO. Вместо этого коэффициенты всё больше приближаются к нулю, но не имеют большого стимула достичь его из-за природы регуляризации L2.

Сравнение ошибок в регрессии лассо (слева) и гребневой регрессии (справа). Поскольку гребневая регрессия использует регуляризацию L2, ее площадь напоминает круг, тогда как регуляризация лассо L1 рисует прямые линии. Свободное изображение. Источник
В лассо улучшение от ошибки 5 до ошибки 4 взвешивается так же, как улучшение от 4 до 3, а также от 3 до 2, от 2 до 1 и от 1 до 0. Следовательно, больше коэффициентов достигает нуля и устраняется больше признаков.
Однако в гребневой регрессии улучшение от ошибки 5 до ошибки 4 вычисляется как 5² − 4² = 9, тогда как улучшение от 4 до 3 взвешивается только как 7. Постепенно вознаграждение за улучшение уменьшается; следовательно, устраняется меньше признаков.
Гребневая регрессия лучше подходит в ситуации, когда мы хотим сделать приоритетными большое количество переменных, каждая из которых имеет небольшой эффект. Если в модели требуется учитывать несколько переменных, каждая из которых имеет средний или большой эффект, лучшим выбором будет лассо.
Реализация
Гребневую регрессию в sklearn можно реализовать следующим образом (см. ниже). Как и для регрессии лассо, в sklearn есть реализация для перекрестной проверки выбора лучших из многих обученных моделей.
5. Регрессия ElasticNet
Теория
ElasticNet стремится объединить лучшее из гребневой регрессии и регрессии лассо, комбинируя регуляризацию L1 и L2.
Лассо и гребневая регрессия представляют собой два различных метода регуляризации. В обоих случаях λ — это ключевой фактор, который контролирует размер штрафа:
Machine Learning – не только нейронки
Нейронные сети и глубокое обучение (deep learning) у всех на слуху, но нейросети – это лишь подобласть такого обширного предмета, как машинное обучение (machine learning). Существует несколько сотен других алгоритмов, которые способны быстро и эффективно решать задачи искусственного интеллекта и в большинстве случаев являются более интерпретируемыми для человека. В этой статье рассмотрим алгоритмы классического машинного обучения, принцип работы нейросетей, подготовку данных для обучения моделей и задачи, которые решают с помощью искусственного интеллекта (ИИ).
Основные задачи машинного обучения
Восстановление регрессии (прогнозирования) – построение модели, способной предсказывать численную величину на основе набора признаков объекта.
Классификация – определение категории объекта на основе его признаков.
Кластеризация – распределение объектов.
Допустим, есть набор данных со статистикой по приложениям. В нем есть следующие сведения: размер, категория, количество скачиваний, количество отзывов, рейтинг, возрастной рейтинг, жанр и цена. С помощью этого набора данных и машинного обучения можно решить такие задачи:
Прогнозирование рейтинга приложения на основе признаков: размер, категория, возрастной рейтинг, жанр и цена – задача регрессии.
Определение категории приложения на основе набора признаков: размер, возрастной рейтинг, жанр и цена – задача классификации.
Разбиение приложений на группы на основании множества признаков (например, количество отзывов, скачиваний, рейтинга) таким образом, чтобы приложения внутри группы были более похожи друг на друга, чем приложения разных групп.
Нейронные сети (многослойный перцептрон)
Существует мнение, что лучшие идеи для изобретений человек заимствует у природы. Нейронные сети – это именно тот случай, ведь сама концепция нейросетей базируется на функциональных особенностях головного мозга.
Принцип работы
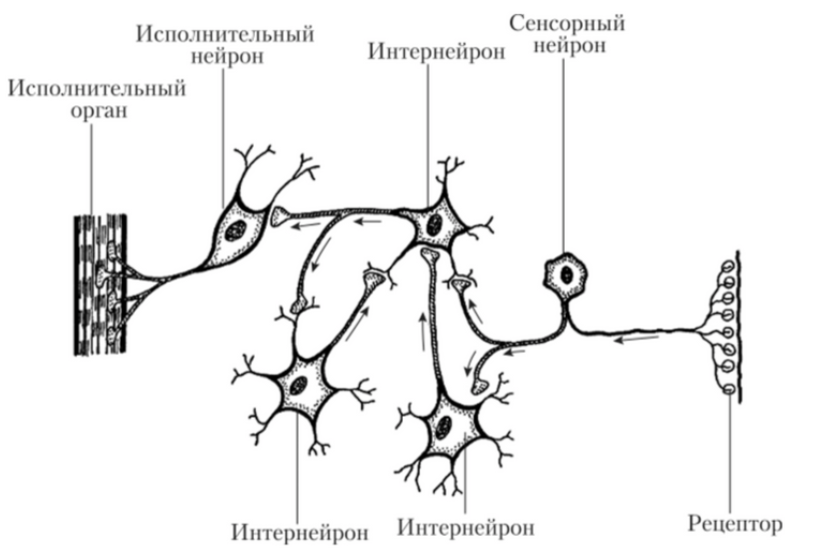
Есть определенное количество нейронов, которые между собой связаны и взаимодействуют друг с другом путем передачи сигналов. Также есть рецепторы, которые получают информацию, поступающую извне, и исполнительный орган, на который приходит итоговый сигнал. По схожему принципу работают искусственные нейросети: есть несколько слоев с нейронами и связи между ними (каждая связь имеет свой весовой коэффициент). По связям передаются сигналы в виде численных значений, первый слой выполняет собой роль рецепторов, то есть получает набор признаков для обучения, и есть выходной слой, который выдает ответ.
Нейронные связи в головном мозге (« Создаем нейронную сеть » , Тарик Рашид)
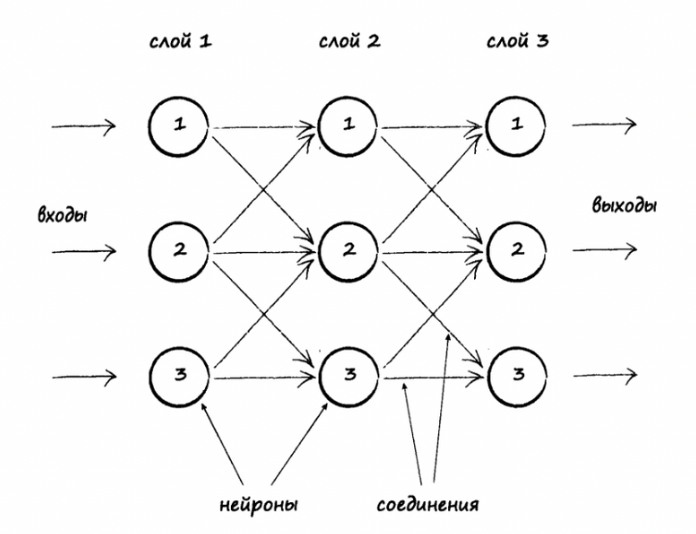
Пример искусственной трехслойной нейросети («Создаем нейронную сеть » , Тарик Рашид)
Каждый слой нейросети оперирует разными представлениями о данных. На рисунке ниже можно увидеть пример использованиям глубокого обучения (нейросети) для распознавания образа на картинке. На входной слой нам поступают пиксели изображений, далее после вычислений между входным и первым скрытым слоем мы получаем границы, на втором скрытом слое – контуры, на третьем – части объектов, на выходном – вероятности принадлежности изображения к каждому типу объектов.
Пример использования нейросети для распознавания образа ( «Глубокое обучение», Ян Гудфеллоу)
Как настраивать
Настраивается путем задания количества узлов, скрытых слоев и выбора функции активации. В искусственных нейронных сетях функция активации нейрона отвечает за выходной сигнал, который определяется входным сигналом или набором входных сигналов.
Какие задачи решают
Нейросети применяют для решения задач классификации, регрессии и кластеризации.
Классические алгоритмы машинного обучения (Machine Learning)
K-ближайших соседей
Метод K-ближайших соседей – простой и эффективный алгоритм, его можно описать известной поговоркой: «Скажи мне, кто твой друг, и я скажу, кто ты».
Принцип работы
Пусть имеется набор данных с заданными классами. Мы можем определить класс неизвестного объекта, если рассмотрим определенное количество ближайших объектов (k) и присвоим тот класс, который имеет большинство «соседей». Посмотрим на рисунок ниже.
Есть набор точек с двумя классами: синие крестики и красные кружки. Мы хотим определить, к какому классу относится неизвестная зеленая точка. Для этого мы берем k ближайших соседей, в данном случае 3, и смотрим, к каким классам они относятся. Из трех ближайших соседей больше оказалось синих крестиков, соответственно, мы можем предположить, что зеленая точка также, скорее всего, относится к этому классу.
Как настраивать
Необходимо подобрать параметр k (количество ближайших соседей) и метрику для измерения расстояний между объектами.
Какие задачи решает
В основном – классификация, но может применяться и для задач регрессии.
Линейная регрессия
Линейная регрессия – простая и эффективная модель машинного обучения, способная решать задачи быстро и недорого.
Принцип работы
Модель линейной регрессии можно описать уравнением y =a0 + a1x1 + a2x2+. +anxn , где x – это значения признаков, y – целевая переменная, a – весовые коэффициенты признаков. При обучении модели весовые коэффициенты подбираются таким образом, чтобы как можно лучше описывалась линейная зависимость признаков от целевой переменной.
Пример: задача предсказания стоимости квартиры в зависимости от площади и удаленности от метро в минутах. Целевой переменной (y) будет являться стоимость, а признаками (x) – площадь и удаленность.
На рисунке ниже также представлен пример построения линейной регрессии. Красная прямая более точно описывает линейную зависимость x от y.
Как настраивать
Для многих моделей Machine Learning, в частности и для линейной регрессии, можно улучшить итоговое качество с помощью регуляризации.
Регуляризация в статистике, машинном обучении, теории обратных задач — метод добавления некоторых дополнительных ограничений к условию с целью решить некорректно поставленную задачу или предотвратить переобучение, то есть ситуацию, когда модель хорошо показывает себя на тренировочный данных, но перестаёт работать на новых.
Распространенные методы регуляризации для повышения качества модели линейной регрессии:
Ridge — один из методов понижения размерности. Применяется для борьбы с переизбыточностью данных, когда независимые переменные коррелируют друг с другом (мультиколлинеарность), вследствие чего проявляется неустойчивость оценок коэффициентов линейной регрессии.
LASSO — также как и Ridge, применяется для борьбы с переизбыточностью данных.
Elastic-Net — модель регрессии с двумя регуляризаторами L1, L2. Частными случаями являются модели LASSO L1 = 0 и Ridge регрессии L2 = 0.
Какие задачи решает
Логистическая регрессия
Логистическая регрессия – также простая и эффективная модель машинного обучения, способная решать задачи быстро и недорого.
Принцип работы
Как настраивать
Как и в случае с линейной регрессией, существуют реализации с коэффициентом регуляризации можно выбрать один из методов регуляризации: Ridge, LASSO, Elastic-Net.
Какие задачи решает
Метод опорных векторов (SVM)
Принцип работы
Чтобы лучше всего понять алгоритм метода опорных векторов, рассмотрим рисунок. На рисунке приведен пример двух линейно разделимых классов в двумерном пространстве. Идея алгоритма заключается в нахождении оптимальной разделяющей прямой (или гиперплоскости для более высоких пространств) для отделения объектов одного класса от другого. Пунктирные линии выделяют разделяющую полосу и проводятся через объекты, которые называют опорными. Чем шире разделяющая полоса, тем качественнее модель SVM. Чтобы определить класс объекта, достаточно определить, с какой стороны гиперплоскости он находится.
Как настраивать
Необходимо подобрать оптимальное ядро (функцию переводящую признаковое пространство в более высокую размерность), если линейная зависимость слабо выражена.
Какие задачи решает
Применяется для решения задач классификации и регрессии.
Сравнение классических алгоритмов с нейросетью
Для примера был взят датасет со статистикой приложений в Play Market. Датасет содержит следующие данные: размер приложения, возрастной рейтинг, количество скачиваний, жанр, категория и др. На данном датасете были обучены модели: линейная регрессия, метод опорных векторов, нейронная сеть (многослойный перцептрон).
В ходе экспериментов были подобраны следующие параметры для моделей машинного обучения:
Линейная регрессия – модели линейной регрессии с регуляризацией не показали результат, превосходящий качество классической линейной регрессии.
Метод опорных векторов – модель метода опорных векторов с RBF-ядром показала лучший результат по сравнению с другими ядрами.
Многослойный перцептрон – оптимальный результат показала модель с 4 слоями, 300 нейронами и функций активацией ReLu. При попытках увеличить количество слоев и нейронов прирост качества не наблюдался.
Была решена задача прогнозирования потенциального рейтинга приложения в зависимости от его признаков.
Результаты ошибки среднего отклонения от истинного значения целевой переменной в процентах для каждой модели:
Линейная регрессия – 6.13 %
Метод опорных векторов – 6.01%
Нейронная сеть – 6.41%
Таким образом, классические алгоритмы машинного обучения и нейросети показали приблизительно одинаковое качество. Это связано с тем, что нейросети хорошо обучаются на датасетах с большим размером и обычно применяются для решения задач, где зависимость в данных очень сложна. Поэтому для решения данной задачи можно обойтись применением классических алгоритмов и не прибегать к использованию нейросетей.
На гистограмме ниже представлены итоговые весовые коэффициенты a, полученные при обучении модели линейной регрессии. Чем больше столбик, тем выше влияние признака на целевую переменную. Если столбик направлен вверх, то он оказывает положительное влияние на рост целевой переменной, если вниз – то отрицательное. Другими словами, если приложение имеет жанр “Other” или “Tools”, то, скорее всего, его рейтинг будет высоким, а если у него категория “FAMILY” или “GAME” – то, вероятно, низким. Данная интерпретация весовых коэффициентов линейной регрессии бывает очень полезной при анализе данных.

Гистограмма значений коэффициентов линейной регрессии
Примеры из нашей практики
Искусственный интеллект и машинное обучение используют для решения бизнес-задач в ритейле, медицине, промышленности и иных отраслях. Мы в своей практике тоже работаем над системами распознавания, компьютерного зрения, предиктивной аналитики. Например, в одном из проектов мы реализовали классификатор, который по фотографии тестера пользователя помогал в диагностике ряда заболеваний.
Познакомьтесь с нашими решениями Machine Learning и другими кейсами в портфолио.