Теория хаоса что это такое простыми словами
Теория хаоса в быту, или Как чашка кофе разрушит вашу жизнь
Согласно теории хаоса, даже небольшие изменения в нашем мире приводят к непредсказуемым последствиям в другом месте и в другое время.
Эдвард Лоренц, основоположник теории хаоса, назвал это явление эффектом бабочки.
Взмах крыла бабочки в Айове вызывает цепочку ошибок и неопределенности, которые нарастают лавинообразно с течением времени и в кульминации приводят к урагану в Индонезии (Эдвард Лоренц). «Эффект бабочки». Композиция в парке скульптур DeCordova (США). Источник фото: Flickr.com
Человеческое поведение — такая же сложная система. Это означает, что одно, само по себе незначительное, действие приводит нас к сложным и непредсказуемым последствиям.
…а вечером обнаруживаете, что времени на важную работу уже не осталось. Это приводит к срыву сроков сдачи или к посредственному качеству работы. Срыв сроков и посредственная работа в свою очередь станут причиной для последующих событий. И так далее.
Как незначительные события приводят к грандиозным последствиям
Каждое наше действие или решение, так же, как и взмах крыла бабочки, имеет множество значительных и непредсказуемых последствий. Некоторые из них позитивные — они помогают структурировать нашу жизнь и достигать целей, а другие, наоборот, негативные — создают хаос и лишают чувства контроля. Поэтому критически важно осознанно выявлять события, обладающие эффектом бабочки и управлять ими.
Вот еще несколько примеров негативных и позитивных «бабочек»:
Негативные:
Позитивные:
Хорошая новость в том, что понимание этого принципа позволяет управлять «бабочками»: предупреждать появление негативных и превращать в привычки позитивные.
Так и создается дисциплина — не благодаря силе воли, а благодаря действиям, обладающим эффектом бабочки, превращенным в привычку.
Почему грандиозные планы обречены на провал
Понимание этого принципа дает нам точку приложения рычага.
Вычислив событие, обладающее эффектом бабочки, мы можем направить фокус внимания на него. И тогда все остальное изменится само собой или станет значительно проще.
Когда я осознал ценность фокуса и понял, как бездарно сливаю время на текучку, не стал устраивать революцию в своей жизни, потому что знал, что в долгосрочной перспективе это не сработает.
Вместо этого я ввел одно правило: начинать день не с новостей и проверки почты, а с 50-минутного фокус-блока изучения английского.
Как только я это сделал, почувствовал себя дисциплинированнее, мои мускулы фокуса стали сильнее, после этого мне было уже легче добавить еще один фокус-блок творческой работы.
Сравните это с традиционным подходом: многие люди хотят сбросить вес или просто стать сильнее. Идея начать с одного маленького действия — ежедневной 5-минутной зарядки или здорового завтрака не вдохновляет их — они презирают такие цели, считая их незначительными.
Вместо этого они «начинают новую жизнь с понедельника»: покупают абонемент в спортзал и спортивную экипировку, нанимают личного тренера, составляют программу тренировки на 6 дней в неделю и садятся на новомодную детокс-диету…
…и все это для того, чтобы через две недели окончательно выгореть и с чувством вины вернуться к привычному комфортному образу жизни.
Подчиняем хаос
Мы не можем постоянно контролировать свои реакции, но можем контролировать события, которые определяют то, что происходит с нами.
Первый шаг к управлению поведением в том, чтобы начать осознанно замечать негативные «бабочки» и заменять их позитивными. Если ваша жизнь структурирована слабо, вы легко найдете в ней десяток таких событий.
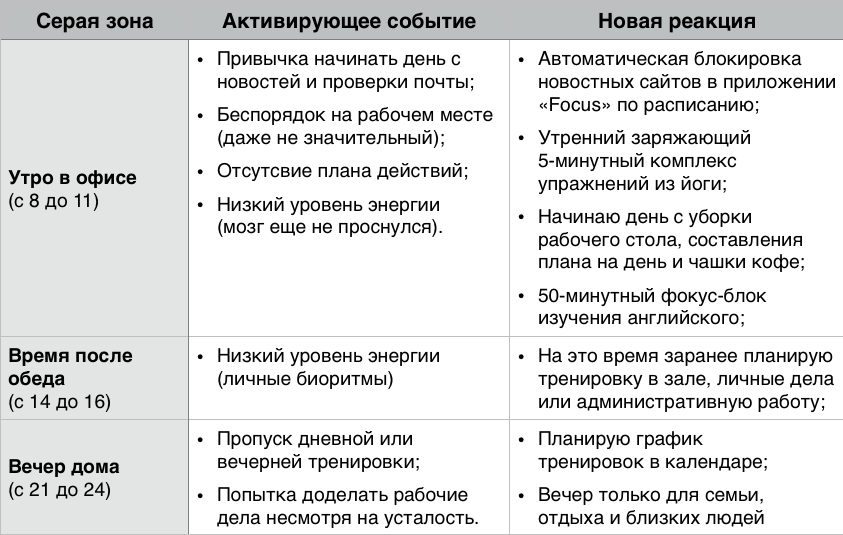
Возьмите лист бумаги и разбейте его на три столбца:
1. В первую колонку выпишите серые зоны — временные блоки, которые проводите вне фокуса: бесцельный интернет-серфинг, непродуктивная поверхностная работа, время с близкими людьми с мыслями о работе.
2. Во второй колонке выявите триггеры, приводящие в серую зону: привычка начинать день с проверки почты, стопка неоплаченных счетов и входящих бумаг в углу рабочего стола, оттягивающая на себя внимание, отсутствие понятного плана действий.
3. В третьей колонке выпишите новые события, которыми вы замените привычные триггеры.
Вот пример одной из моих таблиц:
Таблица помогает выявить события, которые приводят нас в серые зоны, и позволяет осознанно управлять ими.
Так, например, одного осознания факта, что я трачу утреннее время на новости и бесцельный серфинг, для меня оказалось не достаточным. Утром я просто не мог заставить себя взяться за серьезную творческую работу: мой мозг как будто еще не проснулся до конца и все внутри меня сопротивлялось этому. По-настоящему продуктивным я становился только ближе к 11 утра.
Тогда я добавил несколько простых действий, которые позволили переломить ситуацию:
Теперь к 12:00 я успеваю выполнить все самые важные дела, а раньше в это время мог только приступать к работе.
Выводы
1. Человеческое поведение — сложная система. Это означает, что одно, само по себе незначительное, действие приводит нас к сложным и непредсказуемым последствиям.
2. Люди допускают ошибку, думая о поведении, как о линейном процессе, в котором каждое действие или решение не зависит от предыдущих и не влияет на последующие. Из-за этого теряется связь между причиной и следствием.
3. Каждое наше действие или решение имеет множество значительных и непредсказуемых последствий. Некоторые из них позитивные — они помогают структурировать нашу жизнь и достигать целей, а другие, наоборот, негативные — создают хаос и лишают чувства контроля.
4. Понимания этого принципа дает нам точку приложения рычага. Вычислив события, обладающие эффектом бабочки и сфокусировавшись на них, мы делаем все остальное значительно проще.
5. Первый шаг к управлению жизнью в том, чтобы начать осознанно замечать «негативные бабочки» и заменять их «позитивными».
6. Мы можем управлять «бабочками»: предупреждать появление «негативных» и превращать в привычки «позитивные». Так создается дисциплина — не благодаря силе воле, а благодаря действиям, обладающим эффектом бабочки, превращенным в привычку.
Теория хаоса
Однажды зимой 1961 года Эдвард Лоренц, метеоролог из Массачусетского технологического института проводил на громоздком и неуклюжем институтском ламповом компьютере простые симуляции погоды с помощью программы, которую сам написал. Он хотел повторить одну конкретную симуляцию, но не стал начинать с нуля — что всегда занимало много времени, — а взял исходные данные с распечатки предыдущего прогона. Он отошел налить себе чашку кофе, оставив компьютер работать, и вернулся, ожидая, что получит на выходе точное повторение предыдущего результата. К удивлению Лоренца, результат повторного прогона имел мало общего с результатом предыдущего.
Сперва Лоренц подумал, что в компьютере перегорела одна из ламп, но вскоре догадался, что все не так просто. Исходные данные, которые он ввел, компьютер округлял с шести знаков после запятой до трех — на распечатке, но не в памяти. Ученый предполагал, что столь малое отклонение — примерно одна тысячная — едва ли окажет существенное влияние на результат. Но именно это и произошло. Едва заметное различие в начальных условиях привело к огромным различиям в результатах.
Научные модели
Чтоб как-то совладать со сложностью природных явлений — к примеру, климата, — ученые создают модели — упрощенные аналоги реальных явлений, позволяющие обнаружить и математически описать те или иные закономерности. Принято считать, что поведение моделей детерминировано: будущее состояние модели может быть полностью выведено из ее нынешнего состояния на основе математических закономерностей. Этот процесс может проходить через множество итераций — повторений, каждое из которых будет использовать результаты предыдущей итерации как исходные данные, позволяя делать все более и более долгосрочные прогнозы.
Именно таким методом пользовался Лоренц в 1961 году. И всего через несколько итераций программа выдала два совершенно разных результата на основе одних и тех же исходных данных, поставив под сомнение всю методологию. Модель, очевидно, повела себя непредсказуемо и произвела случайный результат: она продемонстрировала — хотя такой терминологии тогда еще не существовало — хаотическое поведение.
Чайки и бабочки
Почему симуляция Лоренца повела себя хаотически? Уравнения, используемые в предсказании погоды, описывают изменение некоторых существенных параметров, таких как температура, влажность, скорость и направление ветра. Важная особенность всех этих параметров в их взаимозависимости: например, уровень влажности зависит от температуры, а температура, в свою очередь, — от влажности.
В математических терминах это означает, что переменные являются функциями самих себя, и отношения между ними описываются нелинейными уравнениями, то есть на графике эти уравнения невозможно представить в виде прямой.
Одно из важнейших свойств системы нелинейных уравнений — чувствительность к начальным условиям, которая так удивила Лоренца в 1961 году. Позже он доказал, что эта чувствительность не зависит от сложности, поскольку проявляется и в более простых моделях (например, конвекции), которые описываются всего тремя нелинейными уравнениями. В 1963 году один из коллег метеоролога заметил, что если идеи Лоренца верны, то «чайка одним взмахом крыла может изменить погоду во всем мире». К 1972 году живое существо, способное нарушить баланс в атмосфере, стало еще меньше — вышедшая в этом году статья Лоренца называлась «Может ли взмах крыла бабочки в Бразилии вызвать торнадо в Техасе?». Так появился «эффект бабочки».
Порядок из беспорядка
«Оказывается, за фасадом порядка может скрываться пугающий хаос, — заметил американский ученый и писатель Дуглас Хофштадтер в 1985 году, — а внутри хаоса все равно скрывается пугающий порядок». Хаотические системы непредсказуемы, но это не значит, что их нельзя описать. Они вовсе не беспорядочны в обыденном, бытовом смысле. Уже в 1963 году простая модель конвекции, предложенная Лоренцом, показала поразительную упорядоченность: ее графическим выражением оказался дивной красоты абстрактный рисунок, напоминающий крылья бабочки, линии которого никогда не повторяются и не пересекаются. «Аттрактор Лоренца», как позже назвали изображение, стал первой из многочисленных топологических моделей хаотических систем, в которых плоскости складывались и растягивались, воспроизводя поведение и траекторию нелинейных систем. В 1970 году Бенуа Мандельброт и его коллеги разработали новую — фрактальную — геометрию, в которой появление порядка из хаоса демонстрируется нерегулярными фигурами, имеющими свойство самоподобия — их нерегулярность повторяется независимо от масштаба.
«Если даже в наших часах больше нет механизма, так с чего ему быть в нашем мире?» Иэн Стюарт, британский математик, 1989
Лоренц заключил, что долгосрочное прогнозирование погоды может быть в принципе невозможно, но этим выводы из теории хаотического поведения систем отнюдь не ограничиваются. Сложная система взаимозависимых факторов, определяющая климат, не уникальна — большинство и физических, и биологических систем имеют такой же характер, они описываются нелинейными уравнениями, и, следовательно, их модели будут неизбежно демонстрировать хаотическое поведение. Теория хаоса распространилась на множество научных дисциплин, связанных лишь присущей предметам их изучения беспорядочностью: турбулентность в динамике жидкостей, флуктуации в динамике популяций, циклы заболеваний в эпидемиологии, фибрилляции сердца в физиологии человека, движение планет и звезд в астрономии, потоки машин в городском трафике. С философской точки зрения способность хаотических с виду систем проявлять почти гипнотическую и завораживающе прекрасную упорядоченность позволяет нам надеяться, что Вселенная все-таки познаваема, и смириться с ее почти неприличной беспорядочностью.
Монтировкой теории хаоса по механизму ньютоновских «часов»
Еще в 1960 году большинство ученых, в том числе и Эдвард Лоренц, посчитали бы, что незначительное отклонение в исходных данных не имеет большого значения. До появления теории хаоса предполагалось, что мир в целом работает согласно механистической, детерминистской модели, которую тремя веками раньше предложил Ньютон (словно безмерно сложный часовой механизм). С такой точки зрения природные явления, в частности погоду, сложно предсказать просто потому, что они сами по себе исключительно сложны; но в принципе такое предсказание возможно, если удастся полностью понять все участвующие в формировании явления физические процессы и получить доступ ко всем необходимым данным. И надежность прогнозов, в том числе и метеорологических, зависит исключительно от качества исходных данных. Теория хаоса полностью опровергла это предположение.
Поиски смысла в беспорядке
Термин «эффект бабочки» быстро приобрел широкую популярность, но его истинное значение часто понимают неправильно. Обычно, говоря об «эффекте бабочки», имеют в виду, что зачастую причиной важных событий становятся мелочи, но на самом деле понятие это несколько шире. Взмах крыла бабочки становится причиной торнадо только в ограниченном смысле: торнадо могло бы и не возникнуть, если бы бабочка не взмахнула крылом, но на его появление так или иначе влияют миллионы, если не миллиарды, других факторов. Благодаря «эффекту бабочки» удалось оценить, насколько пугающе чувствительна система в целом даже к самым незначительным происходящим внутри нее событиям. А из этого следует, что определить все причины того или иного события в системе практически невозможно. Если даже совсем незначительные события, в том числе и те, о которых мы в принципе не можем ничего знать, способны вызвать изменения всей системы, вполне вероятно, что полностью детерминированная система окажется при этом совершенно непредсказуемой.
Теория хаоса
Что такое «странные аттракторы» и как они помогают синоптикам
Можно ли прогнозировать хаотическое движение элементов какой-либо системы? От чего зависит хаотическая динамика? Может ли, наконец, взмах крыла бабочки вызвать торнадо? Некоторые важные ответы на эти и другие вопросы нашел американский метеоролог Эдвард Лоренц, (невольный) автор термина «эффект бабочки» и создатель «странного аттрактора». Рассказываем об этом в первом материале, посвященном самым интересным дифференциальным уравнениям.
В 1972 году профессор метеорологии из Массачусетского технологического института Эдвард Лоренц собирался выступить на конференции, но в пылу работы не успел отправить тему своей лекции. Организатор, спешивший разослать приглашения, выбрал заголовок за него: «Предсказуемость: может ли взмах крыла бабочки в Бразилии вызвать торнадо в Техасе?» Так и появился термин «эффект бабочки», известный сегодня всему миру.
Эдвард Лоренц родился в 1917 году в небольшом городке в штате Коннектикут. Изучать атмосферные явления он решил еще в детстве, испытав потрясение от того, с какой легкостью солнечная погода может смениться бурей с громом и молниями.
Путь к исполнению мечты вышел долгим: магистратура в Гарварде, работа метеорологом в авиационном подразделении Армии США, защита диссертации в послевоенный период, наконец, должность научного сотрудника и, позже, профессора в MIT.
В своем выступлении Лоренц выделил несколько ключевых идей:
⦁ Если взмах крыла бабочки может вызвать торнадо, то точно так же на это способны все предыдущие и будущие взмахи, равно как и взмахи остальных миллионов бабочек, не говоря уже об активности бесчисленного населения нашей планеты.
⦁ Если взмах крыла бабочки способен вызывать торнадо, то в равной степени этот же взмах может его предотвратить.
Взмах крыла бабочки в данном контексте должен восприниматься как маленькое изменение начальных условий исследуемой системы, способное как вызвать торнадо, так и изменить его траекторию или вообще стать причиной его затухания.
В отличие от эффекта домино, где конкретное (обычно незначительное) действие приводит к конкретному (обычно значительному) результату, причем происходит это однозначно, взмах бабочки может не иметь никакого влияния на поведение торнадо.
Система Лоренца
Лоренц изучал конвекцию (теплообмен, возникающий за счет движения молекул жидкости или газа) в атмосфере Земли. Для описания подобных физических процессов часто пользуются моделью, которая включает в себя уравнения Навье-Стокса, описывающие движение вязкой ньютоновской жидкости (за исключением некоторых частных случаев, их решения в общем виде на данный момент неизвестны):
⦁ Уравнение движения в векторном виде:
⦁ Уравнение теплопроводности, описывающее распределение температуры в пространстве с течением времени:
⦁ Уравнение непрерывности, которое, по своей сути, описывает принцип сохранения массы чего-либо:
В оригинале эти три составляющие дают следующую систему:
Мы не будем углубляться в детальное объяснение всего вышеизложенного. Достаточно лишь понимать, что это довольно сложная модель, и Лоренцу в результате многостраничных выкладок удалось построить ее упрощение:
Здесь переменная с точкой сверху означает ее производную по времени. Более подробно:
С помощью этой системы уравнений можно рассчитать, как будет вести себя текучая среда, которую равномерно разогревают снизу и охлаждают сверху. Так, как это происходит с воздушными потоками в атмосфере. В частности, она позволяет понять, к какому результату приведет даже небольшое изменение исходных параметров.
Хаотическое движение
Перед тем как приступить к непосредственному анализу полученной системы, рассмотрим некоторые комбинации траекторий. Для наглядности, воспользуемся теми же значениями параметров, что и сам Лоренц: σ = 10, ρ = 28, β = 8/3.
Изобразим движение двух точек, расстояние между которыми изначально невелико:
Довольно интересный результат! Поначалу траектории почти неразличимы, потом они отклоняются совсем ненамного, после чего разница становится уже значительной.
Попробуем еще раз, однако теперь возьмем точки на значительном отдалении друг от друга:
Даже несмотря на подобную разницу начальных условий, траектории попадают на фигуру, которую впоследствии не покидают. Очень странно, их будто что-то притягивает…
Странный аттрактор Лоренца
Действительно, эта фигура так и называется — странный аттрактор Лоренца (от английского attract — «притягивать»).
Формальное математическое определение звучит так: аттрактор — такое подмножество фазового пространства, что все траектории, стартующие не слишком далеко от него, стремятся к нему с течением времени. (Это одно из возможных определений понятия аттрактора, существуют и другие, не эквивалентные данному.)
Слово же «странный» здесь выступает в таком ключе: аттрактор как множество не представим в виде кривой или поверхности, он имеет более сложную, фрактальную структуру. Траектории аттрактора не замыкаются, а малые отклонения постоянно накапливаются, причем экспоненциально.
Сказанное выше можно проиллюстрировать так: две траектории, выпущенные из близких точек, со временем разбегаются достаточно далеко. Причем, чтобы отдалить момент разбегания, например, на одну секунду, нужно уменьшить расстояние между начальными точками, скажем, вдвое. А чтобы на две секунды — вчетверо. А на три — в восемь раз, и так далее.
Это означает, что, даже используя мощный компьютер, мы не можем просчитать траекторию, проходящую вблизи аттрактора, с разумной точностью на протяжении длительного промежутка времени. На каждом шаге вычислений неизбежно вносятся ошибки (из-за округления чисел и погрешностей численных методов), которые быстро накапливаются и приводят к тому, что найденная траектория сильно отличается от настоящей.
Такое искажение невозможно исправить, просто увеличивая мощность компьютера. Подобное явление называется «динамическим хаосом».
Ниже представлена модель странного аттрактора, с которой можно поэкспериментировать, меняя входящие значения. Для желающих более подробно изучить математическую сторону припасен еще один раздел сразу после модели.
Вы можете покрутить модель или увеличить/уменьшить ее масштаб (с помощью кнопок мыши на десктопе или пальцами на экране смартфона). Значение бегунков сверху вниз:
Немного математики
Система Лоренца обладает несколькими замечательными свойствами:
⦁ Правая часть системы не имеет свободных членов, то есть она однородна.
Теория хаоса
Kласс: Это незавершённая статья по ивентологии и её применениям
Теория хаоса гласит, что сложные системы чрезвычайно зависимы от первоначальных условий и небольшие изменения в окружающей среде ведут к непредсказуемым последствиям.
Пионерами теории считаются французский физик и философ Анри Пуанкаре (доказал теорему о возвратах), русские математики А. Н. Колмогоров и В. И. Арнольд, Мозер, построившие теорию хаоса, называемую КАМ (теория Колмогорова-Арнольда-Мозера). Теория вводит понятие аттракторов (в том числе, странных аттракторов как притягивающих канторовых структур), устойчивых орбит системы (т. н. КАМ-торов).
Содержание
Литература
См. также
Ссылки
В экономике
Теория хаоса в последнее время является одним из самых модных подходов к исследованию рынка. К сожалению, точного математического определения понятия хаос пока не существует. Сейчас зачастую хаос определяют как крайнюю непредсказуемость постоянного нелинейного и нерегулярного сложного движения, возникающую в динамической системе. Согласно теории хаоса, если вы говорите о хаотичном движении цены, то вы должны иметь ввиду не случайное движение цены, а другое, особенно упорядоченное движение. Если динамика рынка хаотична, то она не случайна, хотя и по-прежнему непредсказуема. Непредсказуемость хаоса объясняется в основном существенной зависимостью от начальных условий. Применительно к невозможности делать долгосрочные прогнозы погоды существенную зависимость от начальных условий иногда называют «эффектом бабочки». «Эффект бабочки» указывает на существование вероятности того, что взмах крыла бабочки в Бразилии приведет к появлению торнадо в Техасе. Один из главных выводов теории хаоса, таким образом, заключается в следующем – будущее предсказать невозможно, так как всегда будут ошибки измерения, порожденные в том числе незнанием всех факторов и условий. То же самое по-простому – малые изменения и/или ошибки могут порождать большие последствия.
Еще одним из основных свойств хаоса является экспоненциальное накопление ошибки. Согласно квантовой механике начальные условия всегда неопределенны, а согласно теории хаоса – эти неопределенности будут быстро прирастать и превысят допустимые пределы предсказуемости. Второй вывод теории хаоса – достоверность прогнозов со временем быстро падает. Данный вывод является существенным ограничением для применимости фундаментального анализа, оперирующего, как правило, именно долгосрочными категориями.
Первые элементы теории хаоса появились еще в XIX веке, однако подлинное научное развитие эта теория получила во второй половине XX века, вместе с работами Эдварда Лоренца (Edward Lorenz) из Массачусетского технологического института и франко-американского математика Бенуа Б. Мандельброта (Benoit B. Mandelbrot). Эдвард Лоренц в свое время (начало 60-х годов XX века, работа опубликована в 1963 году) рассматривал, в чем возникает трудность при прогнозировании погоды. До работы Лоренца в мире науки господствовало два мнения относительно возможности точного прогнозирования погоды на бесконечно длительный срок. Первый подход сформулировал еще в 1776 году французский математик Пьер Симон Лаплас. Лаплас заявил, что «…если мы представим себе разум, который в данное мгновение постиг все связи между объектами во Вселенной, то он сможет установить соответствующее положение, движения и общие воздействия всех этих объектов в любое время в прошлом или в будущем». Таким образом, Лаплас и его сторонники говорили, что для точного прогнозирования погоды необходимо только собрать больше информации обо всех частицах во Вселенной, их местоположении, скорости, массе, направлении движения, ускорении и т.п. Второй подход к возможности прогнозирования погоды раньше всех наиболее четко сформулировал другой французский математик, Жюль Анри Пуанкаре. В 1903 году он сказал: «Если бы мы точно знали законы природы и положение Вселенной в начальный момент, мы могли бы точно предсказать положение той же Вселенной в последующий момент. Но даже если бы законы природы открыли нам все свои тайны, мы и тогда могли бы знать начальное положение только приближенно. Если бы это позволило нам предсказать последующее положение с тем же приближением, это было бы все, что нам требуется, и мы могли бы сказать, что явление было предсказано, что оно управляется законами. Но это не всегда так; может случиться, что малые различия в начальных условиях вызовут очень большие различия в конечном явлении. Малая ошибка в первых породит огромную ошибку в последнем. Предсказание становится невозможным, и мы имеем дело с явлением, которое развивается по воле случая».В этих словах Пуанкаре мы находим постулат теории хаоса о зависимости от начальных условий.
Последующее развитие науки, особенно квантовой механики, опровергло детерминизм Лапласа. В 1927 году немецкий физик Вернер Гейзенберг открыл и сформулировал принцип неопределенности. Этот принцип объясняет, почему некоторые случайные явления не подчиняются лапласовому детерминизму. Гейзенберг показал принцип неопределенности на примере радиоактивного распада ядра. Так, из-за очень малых размеров ядра невозможно знать все процессы, происходящие внутри него. Поэтому, сколько бы информации мы не собирали о ядре, точно предсказать, когда это ядро распадется невозможно. Какими же инструментами располагает теория хаоса. В первую очередь это аттракторы и фракталы. Аттрактор (от англ. to attract – притягивать) – геометрическая структура, характеризующая поведение в фазовом пространстве по прошествии длительного времени. Здесь возникает необходимость определить понятие фазового пространства. Итак, фазовое пространство – это абстрактное пространство, координатами которого являются степени свободы системы. Например, у движения маятника две степени свободы. Это движение полностью определено начальной скоростью маятника и положением. Если движению маятника не оказывается сопротивления, то фазовым пространством будет замкнутая кривая. В реальности на движение маятника влияет сила трения. В этом случае фазовым пространством будет спираль. Самым простым типом аттрактора является точка. Такой аттрактор характерен для маятника при наличии трения. Независимо от начальной скорости и положения, такой маятник всегда придет в состояние покоя, т.е. в точку. Следующим типом аттрактора является предельный цикл, который имеет вид замкнутой кривой линии. Примером такого аттрактора является маятник, на который не влияет сила трения. Еще одним примером предельного цикла является биение сердца. Частота биения может снижаться и возрастать, однако она всегда стремится к своему аттрактору, своей замкнутой кривой. Третий тип аттрактора – тор. На рисунке 1. тор показан в верхнем правом углу.
Рисунок 1. Основные типы аттракторов. Вверху показаны три предсказуемых, простых аттрактора. Внизу три хаотических аттрактора
Несмотря на сложность поведения хаотических аттракторов, иногда называемых странными аттракторами, знание фазового пространства позволяет представить поведение системы в геометрической форме и соответственно предсказывать его. И хотя нахождение системы в конкретный момент времени в конкретной точке фазового пространства практически невозможно, область нахождения объекта и его стремление к аттрактору предсказуемы. Первым хаотическим аттрактором стал аттрактора Лоренца. На рисунке 1. он показан в левом нижнем углу.
Рисунок 2. Хаотический аттрактор Лоренца
Рисунок 3. Фрактал «ковер Серпинского»
Хаотический аттрактор является фракталом. Как бы мы не изменяли размер аттрактора, он всегда останется пропорционально одинаковым. В техническом анализе типичным примером фрактала являются волны Эллиота, где также работает принцип самоподобия. Дополнительная идея, заложенная во фрактальности, заключается в нецелых измерениях.
Так, в природе вряд ли найдется идеальный шар или куб, следовательно, 3-мерное измерение этого реального шара или куба невозможно и для описания таких объектов должны существовать другие измерения. Скомкайте, например, лист бумаги в комок. С точки зрения классической евклидовой геометрии новообразованный объект будет являться трехмерным шаром. Однако в действительности это по-прежнему всего лишь двумерный лист бумаги, пусть и скомканный в подобие шара. Отсюда можно предположить, что новый объект будет иметь измерение больше 2-х, но меньше 3-х. Это плохо укладывается в евклидовую геометрию, но хорошо может быть описано с помощью фрактальной геометрии, которая будет утверждать, что новый объект будет находиться во фрактальном измерении, приблизительно равном 2.5, т.е. иметь фрактальную размерность около 2.5. Различают детерминистские фракталы, примером которых является ковер Серпинского, и сложные фракталы. При построении первых не нужны формулы или уравнения. Достаточно взять лист бумаги и провести несколько итераций над какой-нибудь фигурой. Сложным фракталам присуща бесконечная сложность, хотя и генерируются простой формулой. Классическим примером сложного фрактала является множество Мандельброта, получаемое из простой формулы 
, где Z и C – комплексные числа и а – положительное число. На рисунке 4. мы видим фрактал 2-й степени, где а = 2.
Рисунок 4. Множество Мандельброта
Динамические переменные принимают значения, которые сильно зависят от начальных условий. При проведенных на компьютере расчетах даже для очень близких начальных значений С итоговые значения могут резко отличаться. Более того, расчеты становятся некорректными, так как начинают зависеть от случайных процессов в самом компьютере (скачки напряжения и т.п.). Таким образом, состояние системы в момент бифуркации является крайне неустойчивым и бесконечно малое воздействие может привести к выбору дальнейшего пути движения, а это, как мы уже знаем, является главным признаком хаотической системы (существенная зависимость от начальных условий). Фейгенбаум установил универсальные закономерности перехода к динамическому хаосу при удвоении периода, которые были экспериментально подтверждены для широкого класса механических, гидродинамических, химических и других систем. Результатом исследований Фейгенбаум стало т.н. «дерево Фейгенбаума».
Рисунок 5. Дерево Фейгенбаума (расчет на основе немного измененной логистической формулы)
Как мы знаем из определения, бифуркации возникают при переходе системы от состояния видимой стабильности и равновесия к хаосу. Примерами таких переходов являются дым, вода и многие другие самые обычные природные явления. Так, поднимающийся вверх дым сначала выглядит как упорядоченный столб. Однако через некоторое время он начинает претерпевать изменения, которые сначала кажутся упорядоченными, однако затем становятся хаотически непредсказуемыми. Фактически первый переход от стабильности к некоторой форме видимой упорядоченности, но уже изменчивости, происходит в первой точке бифуркации. Далее количество бифуркаций увеличивается, достигая огромных величин. С каждой бифуркацией функция турбулентности дыма приближается к хаосу. С помощью теории бифуркаций можно предсказать характер движения, возникающего при переходе системы в качественно иное состояние, а также область существования системы и оценить ее устойчивость.
К сожалению, само существование теории хаоса трудно совместимо с классической наукой. Обычно научные идеи проверяются на основании предсказаний и их сверки с реальными результатами. Однако, как мы уже знаем, хаос непредсказуем, когда изучаешь хаотическую систему, то можно прогнозировать только модель ее поведения. Поэтому с помощью хаоса не только нельзя построить точный прогноз, но и, соответственно, проверить его. Однако это не должно говорить о неверности теории хаоса, подтвержденной как в математических расчетах, так и в жизни. На сейчас еще не существует математически точного аппарата применения теории хаоса для исследования рыночных цен, поэтому спешить с применением знаний о хаосе нельзя. Вместе с тем, это действительно самое перспективное современное направление математики с точки зрения прикладных исследований финансовых рынков.