Трехмерная реальность что это
Десять измерений
Упрощенное объяснение 10 измерений Теории струн.
Представьте, что вы живете в озере. Вы рыба с глазами по обе стороны головы, и все, что вы знаете, это подводный мир растительности и других рыб, плавающих вокруг вас. Солнечный свет проникает, рассеивается и преломляется через воду. Вы в своей жизни убеждены, что этот подводный мир всё, что есть, потому что это всё, что вы можете видеть и ощуать. Тем не менее, существует совершенно новая среда за пределами вашей видимости — та, где животным не нужна вода, чтобы дышать, а цветы расцветают в гораздо более засушливом мире.
Это физическая ситуация, в которой и мы находимся. Мы такие же рыбы, и эти все измерения более трехмерного,— это новые среды, которые мы не можем воспринимать. На самом деле Теория струн, которая пытается примирить относительность с квантовой механикой (законы очень большого с очень малым), работает только в том случае, если предположить, что существует гораздо больше, чем четыре измерения, к которым мы привыкли. Физики верят, но пока не могут доказать, что в Мультивселенной существует до 11 измерений. Да, Мультивселенная, это где вселенные — пузыри, которые иногда объединяются вместе или расходятся. Это разделение пузырей вселенных — одна из возможностей того, что могло бы вызвать Большой взрыв.
Итак, упрощенное изложение 10 измерений Теории струн.
Первое измерение
Линия, соединяющая две точки. Нет ни глубины, ни высоты, только ширина. Это можно назвать осью X.
Второе измерение
Теперь мы добавили высоту или ось Y. Представьте любую плоскую фигуру, например треугольник.
Третье измерение
Теперь мы добавили глубину или ось Z. Это измерение, в котором мы ощущаем окружающий нас мир. Оно включает в себя объем и способность получать поперечные сечения от объектов. Вы можете думать об этом измерении как о пространстве без времени.
Четвертое измерение
Четвертое измерение не является пространственным, а состоит из времени. Время помогает построить местоположение объекта во Вселенной, а также добавляет способ изменения третьего измерения. Помните, мы назвали третье измерение пространством без времени? Ну, теперь у нас официально появилось космическое время.
«Время относительно, ясно? Оно может растягиваться, и оно может сжиматься, но… оно не может бежать назад. Просто не может. Единственное, что может перемещаться по измерениям, например времени, — это гравитация».
– Кристофер Нолан (Christopher Nolan), режиссер ильма Interstellar
Пятое измерение
С этого момента появляются более высокие измерения. Они незаметны для нас, считают ученые, потому что они существуют на субатомном уровне. Эти размеры скручиваются сами по себе в процессе, известном как компактификация. Размеры здесь на самом деле имеют дело с возможностями.
В пятом измерении будет новый мир, который позволит нам увидеть сходства и различия между нашим миром и этим новым, существующим в том же положении и имеющим то же начало, что и наша планета, т. е. в результате Большого взрыва.
Шестое измерение
Шестое измерение — это целая плоскость новых миров, которая позволит вам увидеть все возможные будущие, настоящие и прошлые события с тем же началом, что и наша Вселенная.
Седьмое измерение
В седьмом измерении вплоть до девятого, у нас теперь появляется возможность новых вселенных с новыми физическими силами природы и различными законами гравитации и света. Седьмое измерение — это начало этого, где мы сталкиваемся с новыми вселенными, которые имеют иное начало, чем наше. То есть они появились не в результате Большого взрыва.
Восьмое измерение
Это измерение — плоскость всех возможных прошлых и будущих времен для каждой Вселенной, простирающаяся бесконечно.
Девятое измерение
Девятое измерение раскрывает все универсальные законы физики и условия каждой отдельной Вселенной.
Десятое или одиннадцатое измерение
Некоторые ученые считают, что мультивселенная имеет только 10 измерений, в то время как другие говорят об 11-ти. Однако Мультивселенная не может иметь более 11 измерений из-за собственной консистенции — они становятся неустойчивыми и сворачиваются обратно в 10 или 11 измерений. На данный момент, всё возможно. Есть всё будущее и всё прошлое, все начала и все концы, бесконечно расширенное, измерение всего, что вы можете себе представить. Всё складывается вместе.
В то время как идея мультивселенной забавна с точки зрения научной фантастики и мечтаний, она также математически обоснована и обеспечит основу для Теории всего, что и является попыткой Теории струн. Это было бы прекрасное сочетание науки, математики и мистики.
Измерения 3-4-5
Мы сейчас с вами живем в уникальное, удивительное время. Ведь мы можем жить не только в третьем измерении, как раньше, но и в четвертом, и даже в пятом. Управляя своим фокусом внимания (читайте Сила фокуса внимания), мы можем значительно повысить свои вибрации и сделать свою жизнь совершенно другой, более лучшей, интересной и приятной.
Мы сами можем выбрать – жить ли нам в страхе от всего происходящего в мире, или же выбрать состояние «Все хорошо» и «Все всегда к лучшему» и этим своим внутренним состоянием притягивать в свою жизнь новые события и возможности.
Измерения 3d, 4d, 5d
Теперь о том, что такое измерения и как они классифицируются.
Третье измерение (трехмерная реальность 3d)
Третье измерение – это физический план. Земля, наша родная планета, находится в 3-м измерении. Это не наш истинный дом, как думают многие люди. Это своего рода школа, которая позволяет ускорить рост души через человеческий опыт. И мы в этой школе живем на протяжении многих лет, и многие из людей подчиняются придуманным кем-то идеалам и пытаются соответствовать стандартам. В трехмерной реальности правят инстинкты выживания.
Равновесия и баланса в этой реальности достигнуть довольно сложно, так как на этом плане игра состоит в том, чтобы мы испытывали как можно больше разнополярных эмоций. Эйфория может быстро перейти в гнев или раздражение, радость – в печаль, нетерпение – в апатию, и так далее…Человечество много тысяч лет играло в эту игру, но на данный момент эта игра завершилась, и Земля уже вышла из трехмерной плотности. Поэтому сейчас жизненно важно быть на высоких вибрациях (читайте Как повысить свои вибрации. И зачем их повышать?).
Четвертое измерение (четырехмерная реальность 4d)
Четвертое измерение – это астральный план. Игровая площадка астральных путешественников. 4-е измерение — это также адрес библиотеки Акаши, где каталогизируются все наши действия и переживания (прошлые, настоящие и будущие). Здесь уже работают однополярные светлые энергии, такие как принятие, любовь, благость, радость, доверие, благодарность. В этом измерении уже не надо быть в вечной гонке за материальными ценностями или же, наоборот, уходить в духовность и брать аскезу. Такие полярности здесь не нужны.
В этой мерности человек может заниматься любимым делом, которое будет приносить ему хороший доход без усилий и напряжения. Физически человек может находиться все еще в третьем измерении, а его сознание уже может начать расширяться дальше. В этом измерении происходят интересные вещи. Во-первых, время начинает ощущаться совершенно по-другому. Человек может начать замечать, что если он суетится, бежит, торопится, то время начинает лететь с бешеной скоростью. А если он успокоится, перестает торопиться и суетиться, время как бы тоже замедляется. Не торопясь, без суеты и напряжения человек делает намного больше, чем если бы начал «подгонять» время и торопиться!
А во-вторых, мысль становится на 100% материальной! Многие люди никак не могут понять, почему после просмотра фильма «Секрет» их желания никак не сбываются, хотя они и прописывают их, и визуализируют. А дело все в том, что сначала надо хотя бы немного подняться по вибрациям, выйти из третьего измерения, прекратить жить в режиме выживания и удовлетворения своих базовых потребностей. Лишь бы поесть, поспать, попить пивка и пообсуждать все негативные новости этого мира.
Для быстрой материализации мыслей надо подняться хоть чуть-чуть выше, выйти из коробочки ума и ограничений и посмотреть на мир шире. А для расширения нужны хорошие эмоции и высокие вибрации! Теперь понимаете, почему нужно на хорошей волне (на эту тему советую почитать статью Как привлечь удачу в свою жизнь. Простой и быстрый способ)? У вас появится возможность управлять своим временем и исполнять желания! Не зря в последние годы пошел бум на «позитивное мышление», это была подготовка сознания для перехода в четвертое измерение. Дополнительно советую прочитать статью Исполнение желаний силой мысли. Как это работает сейчас?
! Важно понимать, что сейчас надо обязательно научиться осознанно управлять своим эмоциональным состоянием. Так как если вы по привычке продолжаете проживать какие-то старые программы, выходить из себя по любому поводу, агрессировать и злиться, буквально «засыпать» в негативных реакциях и эмоциях, то вы будете оставаться в третьем измерении. Если же вы будете практиковать состояние «Все Хорошо» (несмотря ни на что!), будете знать что все к лучшему и обращать внимание на свое внутреннее состояние и свои ощущения, то ваши вибрации начнут повышаться, и вы можете в какой-то момент «очутиться» в четвертом измерении. А уж если поднимитесь до пятого – то это будет высший пилотаж! Поистине великолепная игра! Причем невероятно волшебная и приятная.
Пятое измерение (пятимерная реальность 5d)
Пятое измерение – это Божественное пространство безусловной любви, времени не существует на этом плане. Есть только Здесь и Сейчас. В то время как 4-е измерение — это место для открытия, просеивания через весь беспорядок ваших жизненных уроков, кармических связей и т. д. То в 5-ом измерении вы достигаете внутреннего знания, это место крайнего расслабления. Здесь тело все еще остается быть физическим, но более разряженным и менее плотным. Человек, оставаясь в теле, может соединиться со своим Духом, со своим началом, который знает все ответы на все вопросы. Человек может открыть в себе неожиданные безграничные способности.
В этом измерении очень важно иметь открытое сердце, так как здесь правит ее Величество Любовь. Истинная, чистая, безусловная и очень кайфовая! Нет личности, соответственно, нет Эго, из человека изливается чистая любовь. И человек встает на путь служения, отдавая, отдавая, отдавая эту энергию любви. И через это отдавание ее у него становится все больше и больше. Такая безусловная любовь исцеляет на всех уровнях как самого человека, так и окружающее его пространство. Жизнь в измерении 5d – это жизнь в абсолютной энергии любви, это радость и постоянное пребывание в состоянии «Я – Есмь. Все Хорошо».
Вот такие измерения нам сейчас становятся доступны. В каких хотите – в таких живите, управляя своим фокусом внимания и своими вибрациями.
Есть еще более высокие измерения:
Шестое измерение — это смешение духов, физического тела уже нет. Эволюция бытия единого. Фасад отделенности отпадает в 6-м измерении. Идеология «Я ЕСТЬ БОГ» впервые возникает на этом уровне сознания. Любимые тусовки Вознесенных Мастеров, ангелов и наших Высших «Я».
Седьмое измерение — называйте это как хотите: небо, сознание Христа или пробуждение. 7-е измерение не имеет ограничений. Это чистое состояние бытия.
Обратите внимание, где находится ваш фокус внимания. Если вы фокусируетесь на том, как бы выжить, поесть, поспать, обсуждаете людей и негативные новости, то вы живете в третьем измерении. Если вы фокусируетесь на чем-то хорошем, ищете это хорошее во всем, берете ответственность за свою жизнь на себя и понимаете, что практически все в ней зависит от вас, то вы в 4-ом измерении.
А если вы на пути Любви, вы хотите ее бесконечно всем дарить, окружать ею людей, помогать, то вы, вероятно, уже довольно просветленный человек и находитесь в пятом измерении.
Уходите от страха, ничего не бойтесь, радуйтесь, играйте и ЖИВИТЕ, а не существуйте! И прекратите постоянно чего-то ждать, на эту тему читайте статью Чем меньше ожиданий, тем больше радости и счастья!
Благодарю вас за внимание к моей статье и буду благодарна, если подпишитесь на мой Инстаграм! Там много интересного! Жмите на кнопку ниже и подписывайтесь: 
Если эта статья была полезна для Вас, и Вы хотите рассказать о ней своим друзьям, нажмите на кнопочки. БОЛЬШОЕ Спасибо!
Трехмерный мир, в котором мы не живем
Еще древние греки превратили математику из эмпирической науки в дедуктивную, потребовав вывода доказательств ее утверждений из основных понятий и исключив ссылку на опыт в качестве аргумента.
Чистая математика исследует формы и отношения в отвлечении от материального содержания. Ее непосредственным предметом оказываются, например, не те или иные тела шарообразной формы, а «идеальный шар», не те или иные совокупности предметов и даже не отдельные числа, а целые числа вообще и т. п.
Однако при всей абстрактности этой науки никто из математиков, по-видимому, не сомневался в том, что все их понятия, теоремы и формулы выражают реальные количественные и пространственные отношения. Математическая геометрия была теорией реального пространства, как позже механика явилась теорией движения
Математика — наука, изучающая
количественные и пространственные
формы и отношения действительности
Академик А. Д. Александров
Окружающий нас мир трехмерен. Мы привыкли к этой мысли с рождения — каждый человек знает, что такое высота, длина и ширина, три основных измерения окружающего нас пространства. В зависимости от традиций, принятых в разных странах, размеры предметов измеряют в метрах, футах, ли, лье и других эталонных единицах длины. Для наших дальнейших рассуждений выберем немного необычную единицу длины. Ею будет служить один световой год (1 св. г.), т. е. расстояние, проходимое лучом света за один календарный год. В традиционных мерах длины это составляет невообразимую величину — примерно 9,46•10 12 километров.
Если из окружающего нас пространства мысленно вырезать куб с ребром, равным 1 св. году, то внутри благополучно разместится дом, в котором мы живем, земной шар, Солнечная система… В общем, все, что необходимо для нормальной жизни человека. Для удобства назовем рассмотренный нами куб единичным кубом. А теперь отметим следующий очевидный факт. Несмотря на громадные размеры, наш единичный куб — лишь мельчайшая частица окружающего мира.
Кстати сказать, в этом определении размеры самого куба не задаются — вовсе не обязательно использовать кубы больших размеров. С таким же успехом можно утверждать, что каждая точка содержится в кубе, ребро которого не превосходит по длине, скажем, один микрон (10 —6 см).
Все сказанное выше кратко можно выразить следующими словами: окружающий нас мир является трехмерным евклидовым многообразием. А теперь попробуем ответить на следующий вопрос: как устроен мир за пределами единичного куба, в котором находится наш дом — наша Солнечная система?
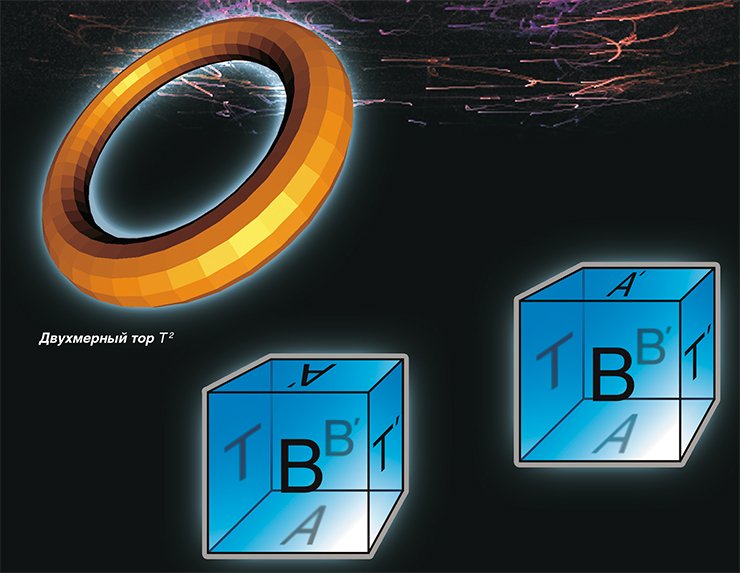
Трехмерный тор и другие
Если на минуту вообразить, что окружающее нас пространство бесконечно по всем направлениям, то ответ на вопрос о строении окружающего нас мира даст следующая теорема Адамара:
«Бесконечно протяженное по всем направлениям трехмерное евклидово многообразие М 3 совпадает с евклидовым пространством E 3 ».
Евклидово пространство Е 3 с прямоугольной системой координат всем хорошо известно, поэтому не будем подробно останавливаться на изучении его свойств.
Для того же, чтобы сделать наши рассуждения более содержательными и интересными, предположим другой вариант: окружающий нас мир замкнут, т. е. имеет конечные размеры и не имеет края. Другими словами, зададимся вопросом, как устроены замкнутые трехмерные евклидовы многообразия, или, другими словами, евклидовы формы. Полный ответ на этот вопрос дает теорема, доказанная Дж. Вольфом (1982):
Существует ровно десять трехмерных евклидовых форм. Причем шесть из них представляют собой ориентируемые, а остальные четыре — неориентируемые многообразия.
Все евклидовые формы строятся схожим образом, единственное — для построения некоторых из них нужно использовать куб, а для других — правильную шестиугольную призму.
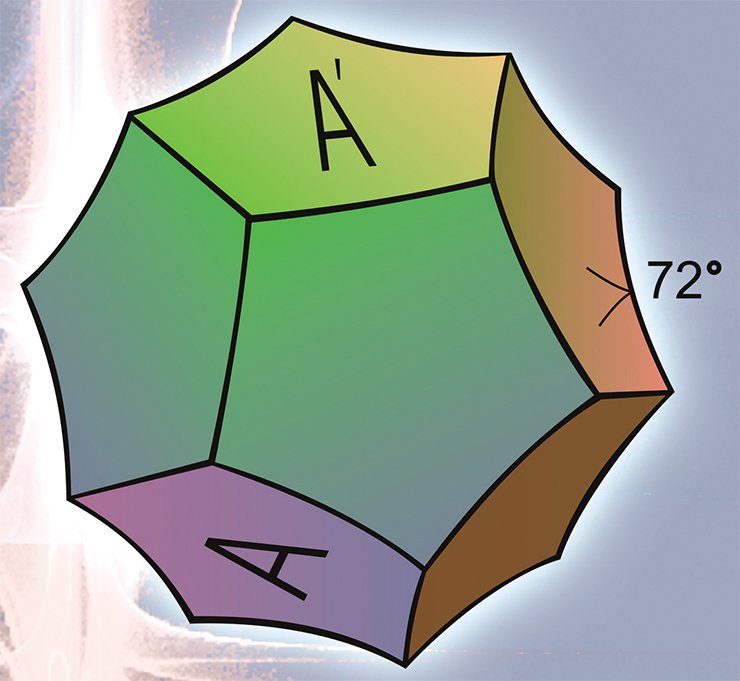
Для этого в центре грани А трехмерного тора поместим космический корабль, летящий со скоростью света, и заставим его стартовать в вертикальном направлении. Ровно через год космический корабль, продолжая двигаться по прямой, вернется в исходную точку. Теперь эта точка будет находиться в центре грани А’, которая, по условию, отождествлена с гранью А. В результате эксперимента обнаружим, что в трехмерном торе Т 3 существует замкнутая прямая линия l длиной в один световой год.
Поставим еще один аналогичный эксперимент. Заставим космический корабль стартовать из точки у, лежащей в грани А на расстоянии 1 км от ее центра. Через год корабль благополучно вернется в точку у. Вывод из второго эксперимента — через точку у проходит замкнутая прямая длиной 1 световой год, параллельная прямой l.
Многообразные многообразия
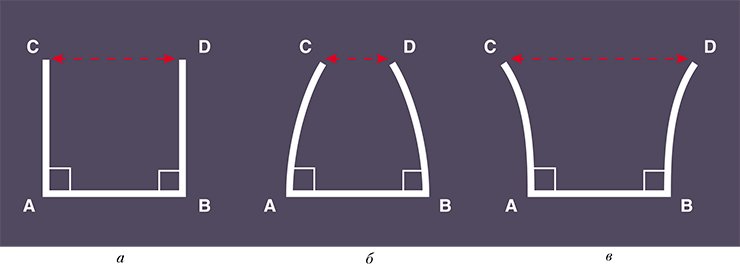
Как уже было замечено, все рассмотренные выше многообразия обладают евклидовой геометрией. Что это означает и какие еще геометрии существуют?
Наиболее известными и употребимыми в общечеловеческой практике являются евклидова, сферическая и гиперболическая геометрии. Напомним, что сферическую геометрию иногда называют геометрией Римана, а гиперболическую — геометрией Лобачевского. В трехмерном пространстве, кроме трех указанных, существует еще пять так называемых синтетических геометрий.
В соответствии с тем, какие геометрические законы действуют на трехмерном многообразии, будем называть его соответственно евклидовым, сферическим, гиперболическим или синтетическим.
Евклидовы многообразия мы уже рассмотрели выше. Что до остальных, то более двадцати лет назад У. Терстон (1978) доказал замечательную теорему: почти все трехмерные многообразия являются гиперболическими, то есть подчиняются законам геометрии Лобачевского. За этот результат в 1983 году он был удостоен Филдсовской премии — самой престижной награды для математиков.
Сферические многообразия бывают как трехмерные, так и многомерные (Вольф, 1982). В пространстве любой размерности существует конечное число типов таких многообразий. Синтетических многообразий очень мало (Thurston, 1978; Dunbar, 1981; Терстон, 2001) в отличие от оставшегося класса гиперболических многообразий. Последний неисчерпаемо широк и классификация его к настоящему времени не завершена.
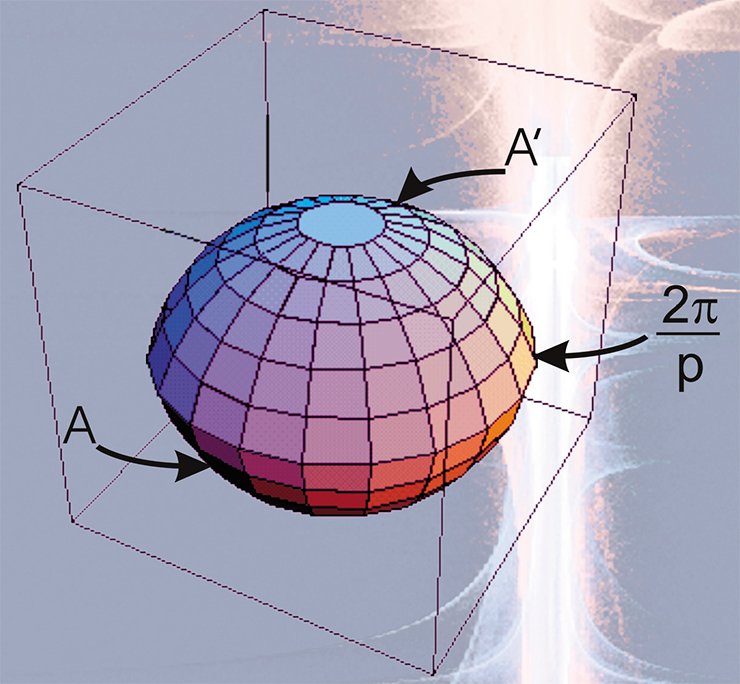
Сферические многообразия
Все трехмерные сферические многообразия — ориентируемы. Это означает, что по какой бы замкнутой траектории не летал космический корабль с непрерывно вращающимся пропеллером, по возвращении в точку старта его пропеллер вращается в ту же сторону, что и в момент старта.
Третий, и пожалуй, самый нетривиальный пример сферического многообразия — сферическое пространство додекаэдра Пуанкаре или, для краткости, сфера Пуанкаре.
Сфера Пуанкаре удивительным образом связана с самыми различными разделами математики — геометрией, топологией, теорией групп, теорией катастроф, теорией узлов и другими (Кирби, Шарлеман, 1982).
Все остальные сферические многообразия, получаемые по единой схеме, представляют собой так называемые линзовые и призматические пространства.
Гиперболические многообразия
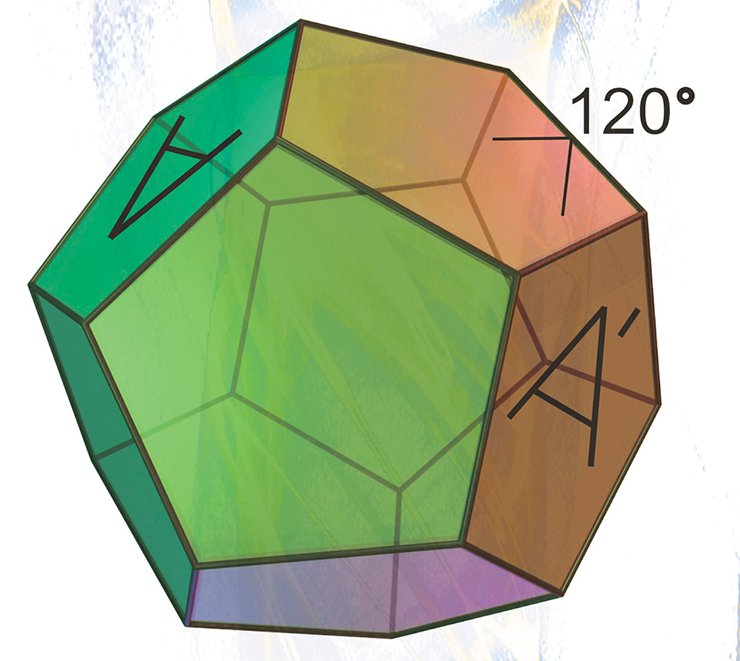
Первое трехмерное замкнутое гиперболическое многообразие было построено немецким математиком Ф. Лебеллем в 1931 г. Однако построение его было достаточно сложным, поэтому двумя годами позже Х. Зейферт и К. Вебер предложили элегантную конструкцию гиперболического пространства додекаэдра.
С точки зрения математики наиболее сложная часть проблемы построения состоит в доказательстве существования этого гиперболического додекаэдра в пространстве Лобачевского. Положительный ответ на этот вопрос дает фундаментальная теорема Е. М. Андреева (1970), в которой сформулированы необходимые и достаточные условия для существования выпуклых гиперболических многогранников. Эта теорема служит одним из краеугольных камней современной теории гиперболических многообразий, созданной У. Терстоном.
Конструируем многообразия из многогранников
Рассмотрим прямоугольный многогранник Р, все двугранные (и плоские) углы которого равны 90°. В евклидовом пространстве в качестве такого многогранника можно взять куб, в сферическом — тетраэдр, а в гиперболическом — шестиугольную призму Лебелля, боковая поверхность которой состоит из 12-ти пятиугольников.
Из теоремы Андреева следует, что любой многогранник, у которого нет треугольных и четырехугольных граней, а в каждой вершине сходится ровно по три ребра, может быть реализован как прямоугольный многогранник в пространстве Лобачевского. Шестиугольная призма Лебелля, очевидно, удовлетворяет этим условиям.
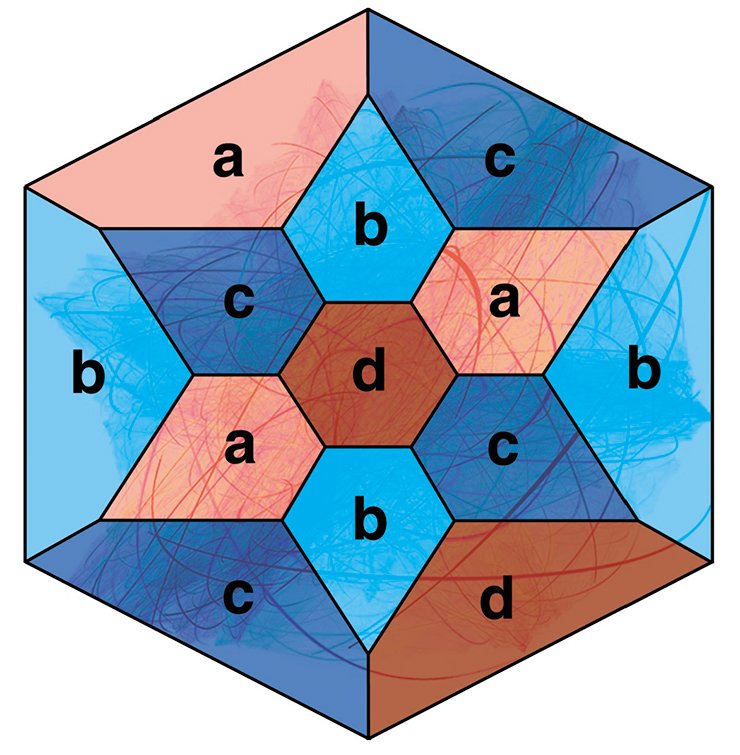
Для построения гиперболических многообразий используется способ, заключающийся в окраске смежных граней многогранника в разные цвета и последующего отождествления соответствующих граней, окрашенных в один цвет, у нескольких одинаковых экземпляров многогранников. Такой способ построения многообразий был впервые реализован Ф. Лебеллем (Loebell, 1931) для шестиугольной призмы, японским математиком М. Такахаши (Takahashi, 1985) — для правильного прямоугольного додекаэдра и А. Ю. Весниным (1987) — для произвольного прямоугольного многогранника Р.
При этом отметим, что все многообразия, построенные по окраске многогранника в четыре цвета, ориентируемы. Однако доказано, что окрашивая грани многогранника Р в пять, шесть или семь цветов, по аналогичной схеме можно построить и неориентируемые многообразия (Mednykh, 1992).
Остановимся еще на одном свойстве прямоугольных многогранников. Пусть D — правильный прямоугольный додекаэдр в пространстве Лобачевского. Испанский математик Х.-М. Монтезинос (Hilden et al., 1987) доказал следующую замечательную теорему:
«Любое замкнутое трехмерное многообразие может быть получено из конечного числа экземпляров многогранника D попарным отождествлением их граней».
Отметим, что в теореме Монтезиноса все грани склеенных многогранников — конгруэнтны, а все ребра имеют одинаковую длину. При этом каждое ребро окружено четырьмя, двумя или одним додекаэдром. Первую ситуацию легко представить: четыре прямоугольных додекаэдра склеены друг за другом вокруг общего ребра и образуют суммарный угол, равный 4•90° = 360°. Во втором случае пара смежных граней одного додекаэдра отождествляется с парой смежных граней другого додекаэдра. Суммарный двугранный угол вокруг ребра, принадлежащего двум додекаэдрам, в этом случае равен 2•90° = 180°. Третий вариант легко создать, отождествляя смежные грани одного додекаэдра поворотом на угол 90°.
Наличие ребер второго и третьего типа превращает многообразие в многообразие с особенностями, или орбифолд. В этом случае указанные ребра образуют сингулярное множество орбифолда. Заметим, что всюду, кроме сингулярных ребер, многообразие обладает геометрией Лобачевского.
Трехмерные орбифолды
Евклидовы орбифолды
Для всякого трехмерного евклидова орбифолда существует фундаментальное множество — криволинейный многогранник, из которого заданный орбифолд можно получить, попарно отождествляя (склеивая) определенные его грани.
Примерами евклидовых орбифолдов могут служить так называемые Борромеевы кольца или трехмерная сфера с сингулярным множеством узел «восьмерка».
Всего существует 230 замкнутых трехмерных евклидовых орбифолдов — по числу кристаллографических групп, открытых в конце прошлого века русским ученым Е. С. Федоровым. Строение евклидовых орбифолдов было полностью описано в докторской диссертации У. Данбара, защищенной в 1981 г. в Принстонском университете — крупнейшем математическом центре мира.
Сферические орбифолды
Сингулярным множеством сферических орбифолдов может служить так называемый рациональный узел или зацепление. Им может оказаться также заузленный граф, из каждой вершины которого выходит по три ребра. В частности, сингулярным множеством сферического орбифолда будет являться скелет тетраэдра (ребра + вершины), расположенный в трехмерной сфере.
q > l. В сферическом пространстве S ³ рассмотрим линзу с углом, равным π/р и поделим ее ребро точками 1,2. 2р на 2р равных частей. Соединим пары точек <р, 2р>и
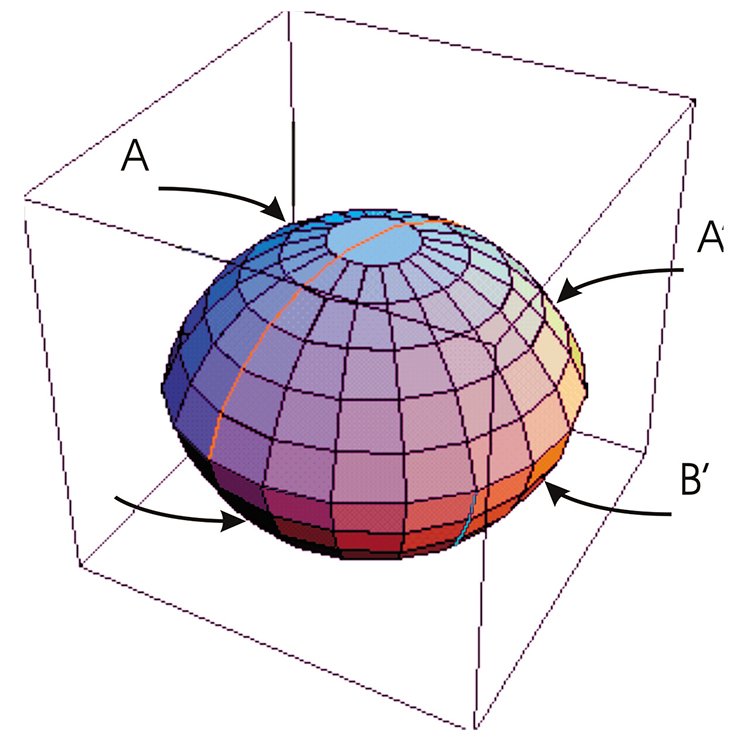
При этом следует иметь ввиду, что сильные заузливания тетраэдра могут испортить сферическую геометрию и заставить орбифолд обладать евклидовой, гиперболической или одной из синтетических геометрий.
Недавно австралийцами профессором К. Ходжсоном и его учеником Д. Хеардом создана компьютерная программа, позволяющая вычислять объемы заузленных графов, вложенных в трехмерную сферу (Hodgson and Heard, 2005). Полная классификация трехмерных орбифолдов во всех геометриях, кроме гиперболической, сделана в работах У. Данбара. Как и в случае многообразий, гиперболическая геометрия является наиболее богатой, и полное описание орбифолдов в ней до сих пор не получено.
Гиперболические орбифолды
Из теоремы Монтезиноса следует, что каждое трехмерное многообразие может быть превращено в гиперболический орбифолд, если внутрь его поместить подходящее сингулярное множество. Поскольку существует бесконечно много различных многообразий, отсюда следует, что существует также бесконечно много гиперболических орбифолдов.
Один из простейших гиперболических орбифолдов — трехмерная сфера с сингулярным множеством Борромеевы кольца с индексом сингулярности 4. Другой пример — сильно заузленный тетраэдр, все ребра которого имеют индекс сингулярности два. Доказательство таких фактов обычно достаточно сложно и может быть проведено с помощью теорем о геометризации, полученных У. Терстоном, его учениками и последователями. Общий принцип доказательства состоит в следующем: если орбифолд не является евклидовым, сферическим или синтетическим и удовлетворяет некоторым простым геометрическим условиям, то он — гиперболический.
Изменения, произошедшие в математике за последние более чем полтора века, не только необозримо расширили ее содержание, но и изменили его принципиально. В предмет математики сейчас входит любая структура, которую можно исследовать путем логического рассуждения с достаточной строгостью и богатством выводов. Найдет ли она применение и прообраз в действительности — это уже вопрос не к математике.
Понятно, что фактически наибольшее развитие получают те теории, которые находят существенные применения в самой математике и тем более за ее пределами. Хотя опыт развития науки уже достаточное число раз показал, как самые отвлеченные теории находили потом чрезвычайно существенные приложения. Но для самой чистой математики это в принципе безразлично. Лучше всего творческое кредо новой математики выразил создатель теории множеств Г. Кантор, гордо зявив: «Сущность математики. в ее свободе».
Винберг Э. Б. О неевлидовой геометрии, Соросовский образовательный журнал, № 3, 1996, С. 104—109.
Тёрстон У. Трехмерная геометрия и топология, М: МЦНМО, 2001 (Перевод с англ. под ред. О. В. Шварцмана).
Hodgson C., Heard D. Computer program “Orb”, August 2005, http://www.ms.unimelb.edu.au/
Работа поддержана грантом РФФИ (№ 06-01-00153) и INTAS (№ 03-01-3663)
Автор и редакция выражает искреннюю благодарность Н. В. Абросимову (вед. инженеру Института математики им. С. Л. Соболева СО РАН, студенту 6-го курса НГУ), оказавшему неоценимую помощь при подготовке публикации