У чего много граней

Основные понятия

Определение многогранника включает в себя такое понятие, как геометрическое тело, созданное из плоских многоугольников. Их число конечное. От формы каждого из них напрямую зависят свойства итоговой фигуры. Их делят на 2 типа:

Поскольку многогранники рассматриваются в трехмерном евклидовом пространстве, они относятся к стереометрии. А их многоугольники лежат в двумерной плоскости, что относится к планиметрии. Поэтому основные свойства и понятия формируются, включая в себя обе эти науки.

Параметры фигуры

Правильные многогранники

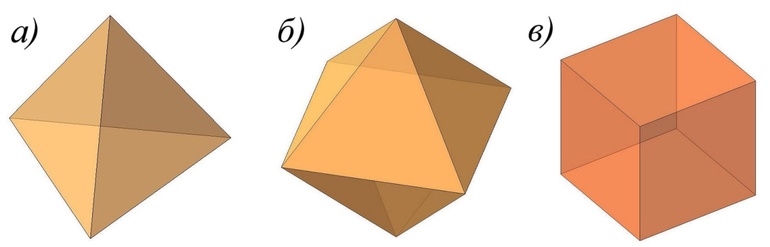
Правильные многогранники — фигуры, грани которых представляют собой многоугольники с равными углами и сторонами. Также они называются Платоновыми телами. Всего существует 5 соответствующих тел, подробные характеристики которых представлены в таблице.

Правильные многогранники изучались древними греками. Однако первые модели в орнаменте и по отдельности появились намного раньше. Например, археологами были найдены вырезанные каменные шары в Шотландии, которые датируются поздним неолитом (соответственно, за 1000 лет до жизни и деятельности Платона).

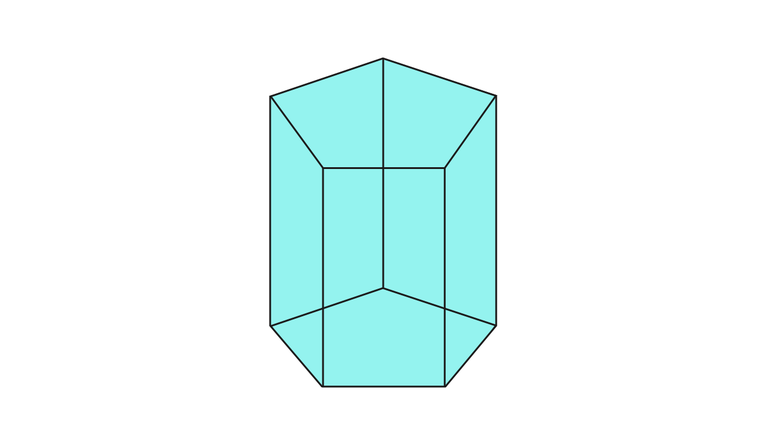
Призма и ее особенности

Геометрическое тело называют прямым, если каждое ребро лежит перпендикулярно основанию. Также они становятся высотами. Когда грани идентичны, многоугольник считается правильным, и его диагональное сечение образует параллелограмм.

Характеристики параллелепипеда

Параллелепипед — многогранник, основанием и гранями которого является параллелограмм. Фигура характеризуется как неправильная. Основные характеристики:

Когда все грани параллелограмма являются прямоугольными, фигура характеризуется, как прямоугольная. Длина каждого ребра считается линейным размером. У такой фигуры есть три измерения. При этом справедлива формула d² = a² + b² + c². При расчетах руководствуются и другими. Для объема : V = abc, для площади многогранника: S=2·(ab+ bc +ac).

Пирамида и ее величины

Пирамида представляет собой многогранник и многоугольник. Особенности фигуры:

Если пирамиду разделяет плоскость, параллельная нижней, она делит ее на две части. Причем верхняя пропорционально равна главной фигуре. Когда основанием является квадрат, геометрическое тело называется правильным. Гранями ее считаются равнобедренные треугольники.

Источник

Правильные многогранники. Часть 1. Трёхмерие

Введение. Постановка вопроса.

В школьной программе, к сожалению, сферическую геометрию и геометрию Лобачевского не изучают. Тем временем, их изучение совместно с Евклидовой геометрией, позволяет глубже понять происходящее с объектами. Например, понять связь правильных многогранников с разбиениями сферы, разбиениями плоскости Евклида и разбиениями плоскости Лобачевского.
Знания геометрии пространств постоянной кривизны помогает подниматься над трёхмерием и выявлять многогранники в пространствах размерности 4 и выше. Вопросы нахождения многогранников, нахождения разбиений пространств постоянной кривизны, вывода формулы двугранного угла правильного многогранника в n-мерном пространстве — так тесно переплетены, что выносить всё это в название статьи оказалось проблематично. Пусть в центре внимания будут, всем понятные, правильные многогранники, хотя они не только результат всех выводов, но и, одновременно, инструмент для постижения пространств высших размерностей и равномерно искривлённых пространств.

Для тех кто не знает (забыл) сообщаю (напоминаю), что в привычном нам трёхмерном Евклидовом пространстве всего пять правильных многогранников:

1. Тетраэдр:	2. Куб:	3. Октаэдр:	4. Додекаэдр:	5. Икосаэдр:

В трёхмерном пространстве правильным многогранником называется выпуклый многогранник, у которого все вершины равны между собой, все рёбра равны между собой, все грани равны между собой и грани являются правильными многоугольниками.

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны.

Вершины равны между собой означает, что количество рёбер и количество граней подходящих к каждой вершине одинаковое и подходят они под одинаковыми углами, в каждой вершине.

Оказывается, правильные многогранники удобно обозначать их символом Шлефли , характеризующим их комбинаторное строение. Который означает, что p1 угольники, сошлись по p2 штук в вершине. Т.е. по определению p1, p2 — целые числа, большие либо равные 3. Для тех кто не знаком с понятием Символ Шлефли написал отдельную статью с картинками Символ Шлефли. Часть 2.6

В такой записи наши многогранники получат обозначения:
1. Тетраэдр <3, 3>,
2. Куб <4, 3>,
3. Октаэдр <3, 4>,
4. Додекаэдр <5, 3>,
5. Икосаэдр <3, 5>
Например, <4, 3>— куб имеет 4 угольные грани, в каждой вершине сходится по 3 таких грани.
У октаэдра <3, 4>наоборот, грани 3 угольные, сходятся по 4 штуки в вершине.
Таким образом символ Шлефли полностью определяет комбинаторное строение многогранника.

Почему правильных многогранников всего 5? Может быть их больше?

Чтобы сполна дать ответ на этот вопрос, нужно сначала получить интуитивное представление о геометрии на сфере и на плоскости Лобачевского. Тем у кого такого представления ещё нет постараюсь дать необходимые объяснения.

Сфера

1. Что такое точка на сфере? Думаю, что всем интуитивно понятно. Мысленно не сложно представить точку на сфере.

2. Что такое отрезок на сфере? Берём две точки и соединяем их кратчайшим расстоянием на сфере, получится дуга, если смотреть на сферу со стороны.

3. Если продолжить этот отрезок в обе стороны, то он замкнётся и получится окружность. При этом плоскость окружности содержит центр сферы, это следует из того, что две исходные точки мы соединили кратчайшим, а не произвольным, расстоянием. Это со стороны она выглядит, как окружность, а в терминах сферической геометрии это прямая, так как была получена из отрезка, продолжением до бесконечности в обе стороны.

4. И, наконец, что такое треугольник на сфере? Берём три точки на сфере и соединяем их отрезками.

По аналогии с треугольником можно нарисовать произвольный многоугольник на сфере. Для нас принципиально важно свойство сферического треугольника, заключающееся в том, что сумма углов у такого треугольника больше 180 градусов, к которым мы привыкли в Евклидовом треугольнике. Более того, сумма углов у двух различных сферических треугольников различна. Чем больше треугольник, тем БОЛЬШЕ у него сумма углов.

Соответственно, появляется 4-й признак равенства треугольников на сфере — по трём углам: два сферических треугольника равны между собой, если у них соответствующие углы равны.

Для простоты саму сферу проще не рисовать, тогда треугольник будет выглядеть немного раздутым:

Сферу ещё называют пространством постоянной положительной кривизны. Кривизна пространства как раз и приводит к тому, что кратчайшим расстоянием является дуга, а не привычный нам прямолинейный отрезок. Отрезок как бы искривляется.

Лобачевский

Теперь, когда мы познакомились с геометрией на сфере, понять геометрию на гиперболической плоскости, открытую великим русским учёным Николаем Ивановичем Лобачевским, будет тоже не сложно, так как тут всё происходит аналогично сфере, только «наизнанку», «наоборот». Если дуги на сфере мы проводили окружностями, с центром внутри сферы, то теперь дуги надо проводить окружностями с центром за пределами сферы.

Приступим. Плоскость Лобачевского будем представлять в интерпретации Пуанкаре II (Жюль Анри́ Пуанкаре́, великий французский учёный), эту интерпретацию геометрии Лобачевского ещё называют диском Пуанкаре.

1. Точка в плоскости Лобачевского. Точка — она и в Африке точка.

2. Отрезок на плоскости Лобачевского. Соединяем две точки линией по кратчайшему расстоянию в смысле плоскости Лобачевского.

Кратчайшее расстояние строится следующим образом:

Надо провести окружность ортогональную диску Пуанкаре, через заданные две точки (Z и V на рисунке). Центр этой окружности будет находиться всегда за пределами диска. Дуга соединяющая исходные две точки будет кратчайшим расстоянием в смысле плоскости Лобачевского.

3. Убрав вспомогательные дуги, получим прямую E1 — H1 в плоскости Лобачевского.

Точки E1, H1 «лежат» на бесконечности плоскости Лобачевского, вообще край диска Пуанкаре — это всё бесконечно удалённые точки плоскости Лобачевского.

4. И наконец, что такое треугольник в плоскости Лобачевского? Берём три точки и соединяем их отрезками.

По аналогии с треугольником, можно нарисовать произвольный многоугольник на плоскости Лобачевского. Для нас принципиально важно свойство гиперболического треугольника, заключающееся в том, что сумма углов у такого треугольника всегда меньше 180 градусов, к которым мы привыкли в Евклидовом треугольнике. Более того, сумма углов у двух различных гиперболических треугольников различна. Чем больше треугольник по площади, тем МЕНЬШЕ у него сумма углов.

Соответственно, тут тоже имеет место 4-й признак равенства гиперболических треугольников — по трём углам: два гиперболических треугольника равны между собой, если у них соответствующие углы равны.

Для простоты сам диск Пуанкаре иногда можно не рисовать, тогда треугольник будет выглядеть немного «усохшим», «сдутым»:

Плоскость Лобачевского (и вообще пространство Лобачевского любой размерности) ещё называют пространством постоянной ОТРИЦАТЕЛЬНОЙ кривизны. Кривизна пространства как раз и приводит к тому, что кратчайшим расстоянием является дуга, а не привычный нам прямолинейный отрезок. Отрезок как бы искривляется.

Правильные разбиения двумерной Сферы и правильные трёхмерные многогранники

Всё сказанное про сферу и плоскость Лобачевского относится к двумерию, т.е. поверхность сферы — двумерна. Какое это имеет отношению к трёхмерию, указанному в заголовке статьи? Оказывается, каждому трёхмерному правильному Евклидову многограннику взаимно однозначно соответствует своё разбиение двумерной сферы. Лучше всего это видно на рисунке:

Чтобы из правильного многогранника получить разбиение сферы, нужно описать вокруг многогранника сферу. Вершины многогранника окажутся на поверхности сферы, соединив эти точки отрезками на сфере (дугами), получим разбиение двумерной сферы на правильные сферические многоугольники. Для примера сделана видео демонстрация как икосаэдр соответствует разбиению сферы на сферические треугольники и обратно, как разбиение сферы на сферические треугольники, сходящиеся по пять штук в вершине, соответствует икосаэдру.

Чтобы по разбиению сферы построить многогранник, соответствующие дугам вершины разбиения нужно соединить обычными, прямолинейными, Евклидовыми отрезками.

Соответственно символ Шлефли икосаэдра <3, 5>— трёхугольники, сходящиеся по пять штук в вершине, задаёт не только структуру этого многогранника, но и структуру разбиения двумерной сферы. Аналогично и с другими многогранниками, их символы Шлефли задают и структуру соответствующих разбиений. Более того, разбиения плоскости Евклида и плоскости Лобачевского на правильные многоугольники, тоже можно задавать символом Шлефли. Например, <4, 4>— четырёхугольники, сходящиеся по четыре — это всем привычная нам тетрадь в клеточку, т.е. это разбиение плоскости Евклида на квадраты. А есть ли другие разбиения плоскости Евклида? Увидим дальше.

Построение разбиений двумерной сферы, плоскости Евклида и плоскости Лобачевского

Для построения разбиений двумерных пространств постоянной кривизны (таково общее название этих трёх пространств) нам потребуется элементарная школьная геометрия и знание того, что сумма углов сферического треугольника больше 180 градусов (больше Пи), что сумма углов гиперболического треугольника меньше 180 градусов (меньше Пи) и что такое символ Шлефли. Обо всём об этом уже сказано выше.

Итак, возьмём произвольный символ Шлефли , он задаёт разбиение одного из трёх пространств постоянной кривизны (для плоскости это верно, для пространств высших размерностей дело обстоит сложнее, но ничто нам не мешает исследовать все комбинации символа).

Рассмотрим правильный p1 угольник, проведём отрезки, соединяющие его центр и вершины. Получим p1 штук равнобедренных треугольника (на рисунке показан только один такой треугольник). Сумму углов каждого из этих треугольников обозначим за t и выразим t через пи и коэффициент лямда.

Тогда если лямда = 1, то треугольник Евклидов, т.е. находится в Евклидовой плоскости, если лямда в интервале (1, 3), то это значит, что сумма углов больше пи и значит этот треугольник сферический (не трудно представить, что при увеличении сферического треугольника в пределе получается окружность с тремя точками на ней, в каждой точке угол треугольника получается равным пи, а в сумме 3*пи. Это объясняет верхнюю границу интервала = 3). Если же лямда в интервале (0, 1), то треугольник гиперболический, так как сумма углов у него меньше пи (т.е. меньше 180 градусов). Коротко это можно записать так:

Не трудно посчитать, что:

С другой стороны, для сходимости в вершине p2 штук (т.е. целого числа) таких же многоугольников нужно, чтобы

Приравнивая выражения для 2*бетта, найденные из условия сходимости и из многоугольника:

Получили уравнение которое показывает какое из трёх пространств разбивает фигура заданная своим символом Шлефли . Для решения этого уравнения надо вспомнить, так же, что p1, p2 — целые числа, большие либо равные 3. Это, так сказать, следует из их физического смысла, так как это p1 угольники (не меньше 3 углов), сходящиеся по p2 штук в вершине (тоже не меньше 3, иначе это не вершина получится).

Решение этого уравнения заключается в переборе всех возможных значений для p1, p2 больших либо равных 3 и вычислении значения лямда. Если оно получится равным 1, то разбивает плоскость Евклида, если больше 1 но меньше 3, то это разбиение Сферы, если от 0 до 1, то это разбиение плоскости Лобачевского. Все эти вычисления удобно свести в таблицу.

Откуда видно, что:
1. Сфере соответствует всего 5 решений, когда лямда больше 1 и меньше 3, они выделены зелёным цветом в таблице. Это: <3, 3>— тетраэдр, <3, 4>— октаэдр, <3, 5>— икосаэдр, <4, 3>— куб, <5, 3>— додекаэдр. Их картинки были представлены в начале статьи.
2. Разбиениям Евклидовой плоскости соответствует всего три решения, когда лямда = 1, они выделены синим цветом в таблице. Вот как выглядят эти разбиения.

3. И наконец, все остальные комбинации соответствуют разбиениям плоскости Лобачевского, соответственно таких разбиений бесконечное (счётное) количество. Осталось только проиллюстрировать некоторые из них, для примера.

Источник

Что такое многогранник? Примеры

Примеры многогранников:

1) каждая сторона одного является одновременно стороной другого (но только одного), называемого смежным с первым (по этой стороне);

Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой его грани.

Из этого определения следует, что все грани выпуклого многогранника являются плоскими многоугольниками. Поверхность выпуклого многогранника состоит из граней, которые лежат в разных плоскостях. При этом ребрами многогранника являются стороны многоугольников, вершинами многогранника – вершины граней, плоскими углами многогранника – углы многоугольников – граней.

Выпуклый многогранник, все вершины которого лежат в двух параллельных плоскостях, называется призматоидом. Призма, пирамида и усеченная пирамида – частные случаи призматоида. Все боковые грани призматоида являются треугольниками или четырехугольниками, причем четырехугольные грани – это трапеции или параллелограммы.

Популярное

Интересный лайфхак, прислала наша читательница из Республики Беларусь.

Ключевым элементом этого проекта является правильная треугольная призма.

Существует концепция, что вершина многогранника отдает энергию, а плоскость энергию принимает. В том случае, если в многограннике вершин больше чем плоскостей, то он обладает.

Для первобытного человека когда-то костер стал новой формой общественной жизни. Ночь перестала быть неотвратимым черным провалом и ценность огня заставила.

Находясь в компании модной одежды и аксессуаров, многогранник чувствует себя вполне уверенно.

Источник

У чего много граней

Кратко охарактеризуем геометрические свойства некоторых многогранников:

а) модель		б) эпюр
Рисунок 67. Пирамида

2. Призма — многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом (рис. 68).

а) модель		б) эпюр
Рисунок 68. Призма

3. Призматоид — многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его основаниями); его боковые грани представляют собой треугольники или трапеции, вершины которых являются и вершинами многоугольников оснований (рис.69).

а) модель		б) эпюр
Рисунок 69. Призматоид

4. Тела Платона. Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными . Углы при вершинах такого многогранника равны между собой.

Существует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим философом Платоном, чем и объясняется их общее название.

Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.

а) модель		б) эпюр
Рисунок 70. Тетраэдр

Гексаэдр — правильный шестигранник (рис. 71). Это куб состоящий из шести равных квадратов.

а) модель		б) эпюр
Рисунок 71. Гексаэдр

Октаэдр — правильный восьмигранник ( рис.72). Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины.

а) модель		б) эпюр
Рисунок 72. Октаэдр

Додекаэдр — правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины (рис. 73).

а) модель		б) эпюр
Рисунок 73. Додекаэдр

Икосаэдр — состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины (рис.74).

а) модель		б) эпюр
Рисунок 74. Икосаэдр

5. Звездчатые формы и соединения тел Платона. Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники.

Источник