Удобные слагаемые это что
Конспект «Разбиение делимого на удобные слагаемые» (3 класс)
Математика, 3 класс
Тема урока: Разбиение делимого на удобные слагаемые.
Тип урока: объяснение нового материала.
1. Научить разбивать делимое на удобные слагаемые.
2. Формировать алгоритм деления на однозначное число, когда делимое представляют в виде суммы удобных слагаемых.
3. Учить отличать удобные слагаемые от разрядных слагаемых.
4. Развивать логическое мышление при изучении нового вычислительного приёма.
5. Отрабатывать вычислительный навык.
— предметные : научить выполнять деление двузначного числа на однозначное (внетабличные случаи деления); отработка вычислительного навыка.
— познавательные: развитие самостоятельного выделения и формулирования познавательной цели, осознанного построения речевого высказывания, выбора наиболее эффективного способа решения, рефлексии способов и условий действия, контроля и оценки процесса и результатов деятельности, анализа объектов, синтеза, постановки и решения проблемы;
— коммуникативные: развитие планирования учебного сотрудничества, умения с достаточной полнотой и точностью выражать свои мысли.
— регулятивные: развитие действия целеполагания, планирования, контроля, коррекции, оценки
— личностные: развитие действия смыслообразования.
Оборудование: интерактивная доска.
Исходный уровень знаний и умений обучающихся для изучения данной темы: знают названия компонентов при делении; знают таблицу умножения и соответствующие случаи деления; умеют представлять многозначное число в виде суммы разрядных слагаемых; знают алгоритм деления суммы на число
Этапы урока и хронометраж:
Математическая разминка. Тест «Пятёрка» – 7 мин.
Подготовка к открытию нового приёма – 7 мин.
А) Создание проблемной ситуации
Б) Формулирование темы и цели урока
Отработка вычислительного навыка по решению примеров вида 68:4 – 10 мин.
Составление и решение задачи с опорой на действие деления – 6 мин.
Деятельность учителя и обучающихся
Учитель: Настроились на серьёзную работу. Сегодня у нас обычный урок, но необычное оценивание вашей работы. У каждого из вас имеется линеечка. Вот по этим ступенькам вы сегодня должны подняться и, чтобы получить хорошую отметку, нужно постараться достигнуть 10-ой ступеньки. А как вы будете подниматься, я буду вам говорить после каждого задания. Ну что же пожелаем друг другу успехов и вперёд за новым знанием.
Линейка для самооценки.
— смыслообразование: новый приём оценивания настраивает на деятельностную работу на уроке
Математическая разминка. Тест «Пятёрка».
Тест «Пятёрка» (вопросы теста написаны на слайде, но задания читает учитель; данный тест детям хорошо знаком) Учитель: Начинаем наш урок с теста «Пятёрка». Напоминаю, что в тесте 5 заданий, у каждого задания 5 вариантов ответа. Вы выбираете один правильный ответ. За данный тест выставляется только отметка «5» тем, кто справится со всеми заданиями, остальные оценку не получают. Итак, слушаем внимательно. 1. Выбери числовое выражение, которое является решением задачи.
В школьный буфет привезли 8кг груш по 13 рублей и столько же яблок по 12 рублей. Сколько стоят все фрукты?
2. Выбери выражение, в котором порядок действий не изменится, если убрать скобки.
4. Выбери верное равенство.
5. Выбери выражение, в котором число представлено в виде суммы разрядных слагаемых.
Учитель: Проверим правильность выполнения данного теста. Напоминаю, что исправлять свои ответы нельзя, а только ставим плюс напротив правильного ответа и минус напротив неверного ответа. (Проверка. Флеш-игра: один ученик выходит к интерактивной доске и в специальной программе выбирает номер правильного ответа, можно вызывать на разные задания разных учащихся).
Учитель: Что сегодня в тесте не получилось. Над чем ещё надо поработать? (Ответы детей) Учитель: Поднимаемся на столько ступенек, сколько у вас правильных ответов.
— нравственно-этическая ориентация: учащиеся учатся объективно проверять и оценивать свою работу.
— умение точно выражать свои мысли в соответствии с задачами.
— контроль: сличение своего результата с заданным эталоном
— оценка: выделение и осознание того, что усвоено и что еще нужно усвоить.
Подготовка к открытию нового приёма.
Учитель: Переходим к следующему заданию. Из чисел 12, 16, 24, 32, 36, 56, 60, 64 выпишите те числа, которые делятся на оба числа, которые записаны в скобках. Внимание: задание выполняется по рядам. Первый ряд выписывает числа, которые одновременно делятся на 4 и 3; второй ряд – на 8 и 2; третий ряд – на 4 и 6. (Задание записано на интерактивной доске).
Учитель: Давайте выберем только внетабличные случаи деления и запишем примеры.
Учитель: Какие из данных примеров мы можем легко вычислить, какие примеры мы уже умеем решать? (Ответы детей: 36:3, 24:2,60:3, 60:6, 64:2)
Учитель: Каким способом мы воспользуемся для вычисления данных примеров? Давайте вычислим их устно. (Дети называют ответы, учитель записывает результат
на интерактивной доске).
— логические универсальные действия: анализ объектов с целью выделения заданных признаков.
— рефлексия способов и условий действия, контроль и оценка процесса и результатов
-контроль: умение сличать свою работу с заданным эталоном;
-коррекция: внесение изменений в случае расхождения.
— логические универсальные действия: действия классификации.
Открытие нового вычислительного приёма вида 45:3:
а) создание проблемной ситуации.
Б) формулирование темы и цели урока.
Учитель: Какие примеры мы не смогли решить? Почему? (Мы такие примеры не решали, не знаем способы вычисления)
Учитель: Я вам предлагаю поработать в группах. Попробуйте совместно найти способ деления оставшихся примеров.
Учитель: На какие числа мы разбивали делимое в примерах, которые решали устно? (Ответы детей: на разрядные слагаемые)
Учитель: Подходит ли данный способ для примеров, которые вы решали в группах? (Ответы детей: нет)
Учитель: У вас получилось найти способ вычисления? (Ответы детей)
Учитель: Сначала заслушаем результаты работы в группах, а потом проверим, у кого совпало решение с моим решением? (На доску прикрепляются варианты решения примеров в группах, учащиеся рассказывают о способах решения).
1 ряд 56:2=(40+16):2=40:2+16:2=20+8=28
2 ряд 60:4=(40+20):4=40:4+20:4=10+5=15
3 ряд 32:2=(20+12):2=20:2+12:2=10+6=16
Учитель: Можно ли числа, на которые разбито делимое назвать разрядными слагаемыми? (Нет) Почему? (Делимое разбито не на разряды: десятки и единицы)
Учитель: А как вы думаете, как принято называть такие числа в математике? (Предположения детей. Если учащиеся не смогут назвать, числа называет учитель)
Учитель: Кто сможет сформулировать тему нашего урока?
Учитель: Какую цель поставим перед собой на сегодняшнем уроке? ( Ответы детей: научиться решать примеры, разбивая их не на разрядные, а на удобные слагаемые)
— постановка и решение проблемы: самостоятельное создание способов решения проблемы;
— общеучебные универсальные действия: выбор наиболее эффективного способа решения заданных примеров;
— самостоятельное создание алгоритма своей деятельности при решении проблемы;
— получают новые знания в процессе работы в группе
— целеполагание: для открытия нового приёма дети вспоминают, что уже им известно и, что на основе известного можно открыть.
— планирование учебного сотрудничества в группе;
— умение с достаточной полнотой и точностью выражать свои мысли
— контроль: умение сличать результат своей деятельности с заданным эталоном;
— коррекция – внесение необходимых дополнений и корректив в способ действия в случае расхождения эталона и его результата.
— формулирование темы урока
— целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися и того, что ещё неизвестно.
(Флеш-игра на интерактивной доске)
Учитель: Мы немного отдохнём, а заодно посмотрим, кто хорошо умеет раскладывать числа на разрядные слагаемые и уже может разбивать делимое и на удобные слагаемые.
(Учащиеся выходят по одному к доске и перетаскивают примеры в нужный сектор. Остальные, если согласны – хлопают, не согласны – топают).
удобные слагаемые разрядные слагаемые
— логические УУД: действия классификации.
— действия контроля и коррекции в случае необходимости
Отработка вычислительного навыка о решению примеров вида 68:4
Учитель: Прочитаем задание. На какие две группы по способу деления можно разбить данные примеры? Выбрать примеры, где делимое будем разбивать на разрядные слагаемые.
Учитель: Решим эти примеры устно.
Учитель: На какие числа будем разбивать делимое в оставшихся примерах? (На удобные слагаемые)
Учитель: Давайте посмотрим, как с данным заданием справились ребята. Кто выбрал самый удобный способ деления и почему? (Ответы детей)
Учитель: Переходим к письменным вычислениям.
а) Решение примеров у доски с подробной записью: 45:3 78:6
б) Самостоятельное решение примеров: 75:5 36:2(для слабых детей заготовлены карточки – помощники: 75:5=(50+…):5, 36:2=(…+16):2)
в) задание под цифрой 5) для тех, кто быстро справится с примерами (с этим заданием справились сильные дети)
Учитель: Кто самостоятельно справился с новыми примерами, поднимается на 2 ступеньки. Если обращались за помощью к учителю или к карточкам-помощникам, поднимаемся на одну ступеньку.
— выбор наиболее эффективного способа решения.
— умение грамотно выражать свои мысли.
— рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности
Составление и решение задач с опорой на действие деления.
Учитель: Составьте простую задачу, используя данные о продолжительности жизни некоторых животных. Задача должна решаться действием делением.
Учитель: Поднимите руку, у кого получилось составить такую задачу, чтобы она решалась действием делением. (Ответы детей).
Учитель: Можно ли составить задачу, чтобы её решением было деление, в котором делимое разбивается на удобные слагаемые? (Ответы детей)
Учитель: Кто составил и решил задачу, поднимается на 1 ступеньку.
— общеучебные УУД: осознанное построение речевого высказывания в устной форме. Задание «Составь задачу»
— логические УУД: синтез – составление целого из частей
Учитель: Какую цель мы ставили на уроке?
Учитель: Поднимите руку,
у кого получилось за один урок научиться разбивать делимое на удобные слагаемые.
Учитель: Кто покорил линеечку и считает, что ему сегодня за урок надо поставить 5?
Учитель: Что было сложно сегодня на уроке?
Учитель: Над чем надо ещё поработать?
— осознание личной самооценки
-осознание качества и уровня усвоения материала по новой теме
— учатся грамотно формулировать свой ответ, правильно делать вывод
И.И. Аргинская, Е.И. Ивановская, С.Н. Кормишина «Математика» 3 класс, часть 2. Самара: Изд. «Учебная литература», 2009
И.И. Аргинская «Сборник заданий по математике». Самара: Изд. «Учебная литература», 2010
Гулюгина М.О. «Формирование тестовой культуры». Волгоград: Изд. «Учитель», 2008
Деменева Н.Н., Тивикова С.К., Яшина Н.Ю. «Требования к современному уроку в начальной школе в соответствии с ФГОС НОО и методические рекомендации по выполнению проекта урока». Н.Новгород: Нижегородский институт развития образования, 2014
Т.А. Лавриненко «Задания развивающего характера по математике». Саратов: Изд. «Лицей», 2003
«Как проектировать универсальные учебные действия в начальной школе» под редакцией А.Г. Асмолова. Москва: Изд. «Просвещение», 2010
«Сборник тестов для оценки качества знаний выпускников начальной школы». Москва: Изд. «Аркти», 2008
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Скоростное чтение
Курс повышения квалификации
Актуальные вопросы теории и методики преподавания в начальной школе в соответствии с ФГОС НОО
Ищем педагогов в команду «Инфоурок»
Номер материала: ДВ-231972
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Совфед отклонил закон о верифицированных онлайн-платформах и учебниках
Время чтения: 2 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
В Москве новогодние каникулы в школах могут начаться с 27 декабря
Время чтения: 1 минута
Росприроднадзор призвал ввести в школах курс по экологии
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.
Представь части домика как слагаемые и сумму.
Как найти неизвестное слагаемое
Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
Нужно из суммы вычесть первое слагаемое.
Неизвестно первое слагаемое.
Как его можно найти?
Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
Перестановка слагаемых
Сделаем запись к рисунку.
3 + 2 = 5
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
2 + 3 = 5
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
Вывод: два соседних слагаемых можно заменить их суммой.
Поделись с друзьями в социальных сетях:
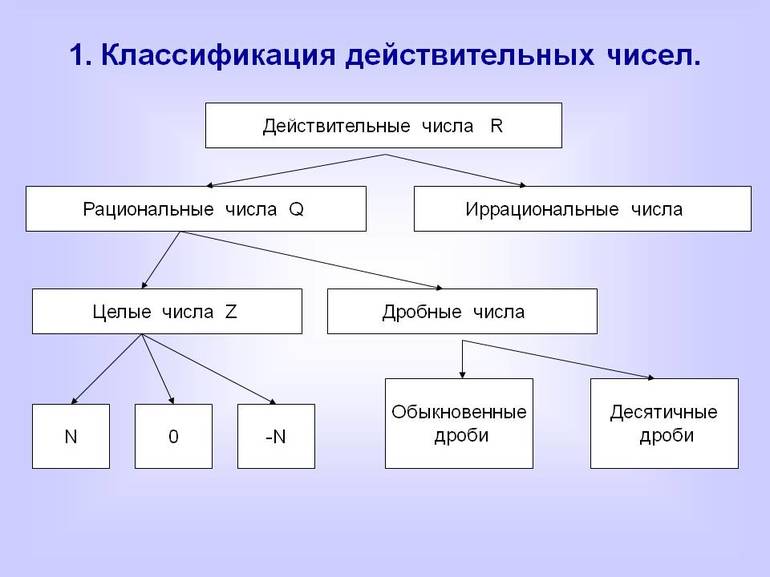
Натуральные числа и их классификация
Натуральными называют естественные величины, которые используются для счета (цифры и их комбинации: 1, 2, 3, 4, 5 и так далее), а также для расстановки по очереди (порядковые числительные: первый, второй, третий, четвертый и так далее). В совокупности они образуют так называемый ряд натуральных чисел. Его обозначением служит латинская буква N.
Главной особенностью этого ряда считается его бесконечность. Она обусловлена тем, что самого большого числа не существует. У любой составляющей ряда есть «старшие товарищи» — величины, которые по своему значению больше.
Распределение по категориям
Составляющие ряда натуральных чисел подразделяются на разряды и классы. Каждая из этих категорий неразрывно связана с другими. Разрядная классификация состоит из следующих групп (в скобках приведены слагаемые, соответствующие каждому разряду):
Разряд числа — это положение, которое оно занимает в цифровой записи. Таким образом, любое числовое значение можно представить посредством разрядных слагаемых по математической формуле следующего вида: nnnn = n000 + n00 + n0 + n, где n означает любую цифру от 0 до 9. Для наглядного примера стоит разбить на составляющие число 4698 = 4000 + 600 + 90 + 8. Получается, что оно состоит из четырех разрядов, отображенных соответствующими составляющими:
Разряд первого слагаемого называют высшим. Цифра, которой он обозначается, всегда больше нуля. Количество разрядов числа, как и количество его разрядных составляющих, всегда соответствует количеству в нем цифр, отличных от 0. Например, число 7052 состоит из трех разрядов, несмотря на свою четырехзначность. Это связано с тем, что в его составе отсутствуют сотни. Его слагаемые — семь тысяч, пять десятков и две простых единицы (7000 + 50 + 2 = 7052).
Разрядные составляющие — это натуральные числа, содержащие только одну цифру, отличную от нуля. Примеры разрядных слагаемых: 7, 30, 200, 4000 и тому подобные. Числа такого вида, как 12, 21, 475, 3500 и так далее, не могут быть отнесены к этой категории. Они подлежат математическому разложению на составляющие.
Название разрядных слагаемых обусловлено принадлежностью каждого из них к определенному разряду. Тысяча считается единицей четвертого разряда, сотня — единицей третьего разряда, десяток — второго, единица — первого. То есть нумерация разрядов начинается от наименьшей составляющей. Единицы первого разряда называются простыми, так как они однозначные. Составляющие прочих разрядов относятся к составным.
Каждый разряд состоит из десяти единиц, но обозначаться он может только девятью, так как десятая единица обеспечивает переход на следующий более высокий разряд. Не может быть разрядной составляющей типа десяти сотен — эта единица обозначается как одна тысяча.
Комплектация разрядов
В целях упрощения записи представления числа через разрядные составляющие единицы разрядов принято группировать в классы. В состав каждого из них входит три разряда:
Для удобства между классами разрешается ставить пробел. Особенно это необходимо для представлений очень больших величин (от миллиона), чтобы они не выглядели бесконечным набором цифр, и в процессе их разложения не возникло путаницы. На классы число разбивается строго по три цифры справа налево.
Первый класс — это единицы. Он включает от одного до трех разрядов. Это значит, что к нему относятся все натуральные числа от 1 до 999. Второй класс — это тысячи. В него входят от четырех до шести разрядов. То есть единицы, принадлежащие к этому классу, есть во всех величинах от 1000 и больше. Дальнейшее распределение по классам:
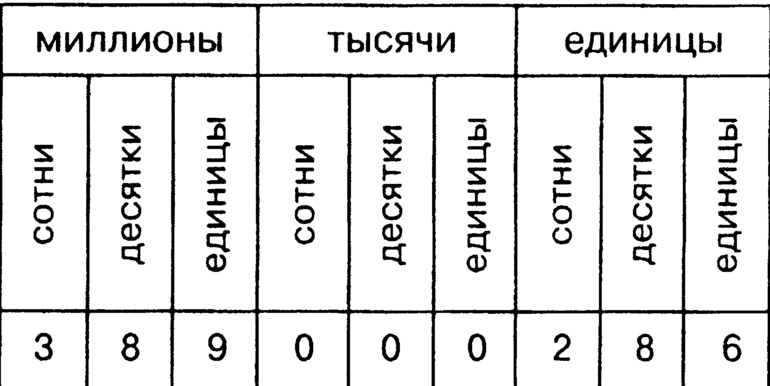
Распределение по классовым и разрядным категориям отображено в таблице:
Особенности разложения
Чтобы лучше понять, что такое разрядные слагаемые в математике и как их использовать, стоит подробно рассмотреть процесс разложения натуральных величин на эти составляющие. В основе большинства задач с разрядными слагаемыми лежит разложение натурального числа, то есть его представление в виде суммы разрядов через сложение количеств всех разрядных единиц.
Преобразить в сумму разрядных слагаемых можно каждую натуральную величину составного типа, то есть многозначную (двузначную, трехзначную и так далее). Чтобы разложить число на разрядные слагаемые корректно, необходимо соблюдать основные правила. Первое — нули не учитываются в разрядном составе числа. Второе — слагаемые записываются в порядке старшинства, то есть от старшего к младшему — вначале тысячи, затем сотни и десятки, последними фиксируются простые единицы.
Разрядный состав можно записать в трех вариантах разбора:
Вне зависимости от выбранного способа разложить число на составляющие по разрядам не составит особого труда. Конечно, чем больше число, тем выше риск запутаться и совершить ошибку. Упражняться лучше сперва на двузначных числах, а затем постепенно повышать разрядность.
Упражнения для тренировки
Для лучшего усвоения материала стоит разобрать несколько тренировочных упражнений. Несколько примеров, какими бывают математические задания по этой теме:
Нередки упражнения с обратным процессом, то есть такие, в которых нужно найти число по его составляющим:
Стоит отметить, что не все задачи с разрядными составляющими решаются путем сложения. Многие упражнения содержат прием их вычитания. Но сложными такие задания кажутся только на первый взгляд. Их суть проста. В скобках приводятся составляющие двух чисел — уменьшаемого и вычитаемого. Требуется найти их разность: (500 + 40 + 1) — (400 + 20) = (100 + 20 + 1) = 121.
Процессы разложения чисел по разрядам и обратного сложения имеют огромное значение для решения различных математических задач и упражнений. Очень важно уметь быстро раскладывать числа любой величины по разрядному составу. Это умение поможет в устном счете и оперировании многозначными числами.
Изучение натуральных чисел и разрядного состава входит в базовую программу по математике. Этот материал проходится учащимися в начальных классах школы.