алгоритмы классификации в машинном обучении

Обзор методов классификации в машинном обучении с помощью Scikit-Learn

Авторизуйтесь

Обзор методов классификации в машинном обучении с помощью Scikit-Learn

Для машинного обучения на Python написано очень много библиотек. Сегодня мы рассмотрим одну из самых популярных — Scikit-Learn.

Scikit-Learn упрощает процесс создания классификатора и помогает более чётко выделить концепции машинного обучения, реализуя их с помощью понятной, хорошо документированной и надёжной библиотекой.

Что такое Scikit-Learn?

Scikit-Learn — это Python-библиотека, впервые разработанная David Cournapeau в 2007 году. В этой библиотеке находится большое количество алгоритмов для задач, связанных с классификацией и машинным обучением в целом.

Scikit-Learn базируется на библиотеке SciPy, которую нужно установить перед началом работы.

Основные термины

В системах машинного обучения или же системах нейросетей существуют входы и выходы. То, что подаётся на входы, принято называть признаками (англ. features).

Признаки по существу являются тем же, что и переменные в научном эксперименте — они характеризуют какой-либо наблюдаемый феномен и их можно как-то количественно измерить.

Когда признаки подаются на входы системы машинного обучения, эта система пытается найти совпадения, заметить закономерность между признаками. На выходе генерируется результат этой работы.

Этот результат принято называть меткой (англ. label), поскольку у выходов есть некая пометка, выданная им системой, т. е. предположение (прогноз) о том, в какую категорию попадает выход после классификации.

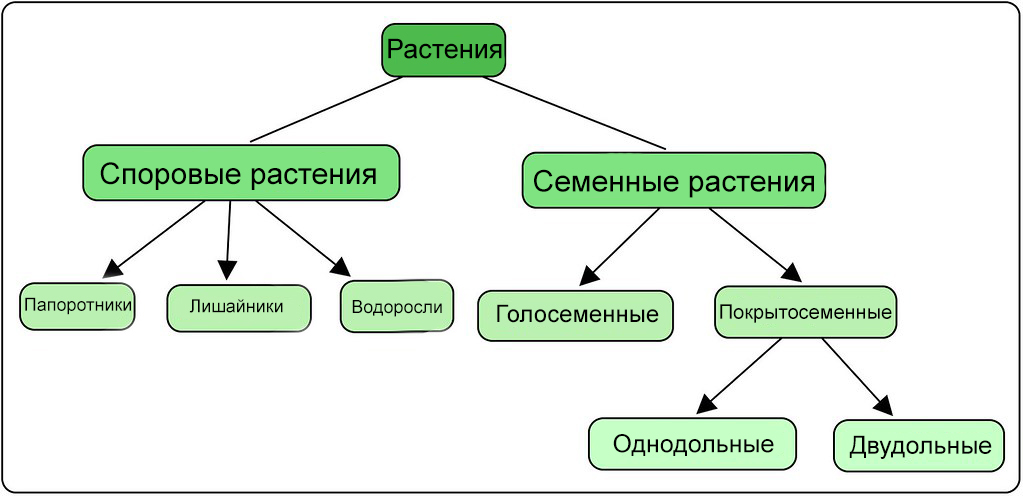
В контексте машинного обучения классификация относится к обучению с учителем. Такой тип обучения подразумевает, что данные, подаваемые на входы системы, уже помечены, а важная часть признаков уже разделена на отдельные категории или классы. Поэтому сеть уже знает, какая часть входов важна, а какую часть можно самостоятельно проверить. Пример классификации — сортировка различных растений на группы, например «папоротники» и «покрытосеменные». Подобная задача может быть выполнена с помощью Дерева Решений — одного из типов классификатора в Scikit-Learn.

При обучении без учителя в систему подаются непомеченные данные, и она должна попытаться сама разделить эти данные на категории. Так как классификация относится к типу обучения с учителем, способ обучения без учителя в этой статье рассматриваться не будет.

Процесс обучения модели — это подача данных для нейросети, которая в результате должна вывести определённые шаблоны для данных. В процессе обучения модели с учителем на вход подаются признаки и метки, а при прогнозировании на вход классификатора подаются только признаки.

Принимаемые сетью данные делятся на две группы: набор данных для обучения и набор для тестирования. Не стоит проверять сеть на том же наборе данных, на которых она обучалась, т. к. модель уже будет «заточена» под этот набор.

Типы классификаторов

Scikit-Learn даёт доступ ко множеству различных алгоритмов классификации. Вот основные из них:

На сайте Scikit-Learn есть много литературы на тему этих алгоритмов с кратким пояснением работы каждого из них.

Метод k-ближайших соседей (K-Nearest Neighbors)

Этот метод работает с помощью поиска кратчайшей дистанции между тестируемым объектом и ближайшими к нему классифицированным объектами из обучающего набора. Классифицируемый объект будет относится к тому классу, к которому принадлежит ближайший объект набора.

Классификатор дерева решений (Decision Tree Classifier)

Этот классификатор разбивает данные на всё меньшие и меньшие подмножества на основе разных критериев, т. е. у каждого подмножества своя сортирующая категория. С каждым разделением количество объектов определённого критерия уменьшается.

Классификация подойдёт к концу, когда сеть дойдёт до подмножества только с одним объектом. Если объединить несколько подобных деревьев решений, то получится так называемый Случайный Лес (англ. Random Forest).

Наивный байесовский классификатор (Naive Bayes)

Такой классификатор вычисляет вероятность принадлежности объекта к какому-то классу. Эта вероятность вычисляется из шанса, что какое-то событие произойдёт, с опорой на уже на произошедшие события.

Каждый параметр классифицируемого объекта считается независимым от других параметров.

Линейный дискриминантный анализ (Linear Discriminant Analysis)

Этот метод работает путём уменьшения размерности набора данных, проецируя все точки данных на линию. Потом он комбинирует эти точки в классы, базируясь на их расстоянии от центральной точки.

Этот метод, как можно уже догадаться, относится к линейным алгоритмам классификации, т. е. он хорошо подходит для данных с линейной зависимостью.

Метод опорных векторов (Support Vector Machines)

Работа метода опорных векторов заключается в рисовании линии между разными кластерами точек, которые нужно сгруппировать в классы. С одной стороны линии будут точки, принадлежащие одному классу, с другой стороны — к другому классу.

Классификатор будет пытаться увеличить расстояние между рисуемыми линиями и точками на разных сторонах, чтобы увеличить свою «уверенность» определения класса. Когда все точки построены, сторона, на которую они падают — это класс, которому эти точки принадлежат.

Логистическая регрессия (Logistic Regression)

У каждого признака есть своя метка, равная только 0 или только 1. Логистическая регрессия является линейным классификатором и поэтому используется, когда в данных прослеживается какая-то линейная зависимость.

Примеры задач классификации

Задача классификации — эта любая задача, где нужно определить тип объекта из двух и более существующих классов. Такие задачи могут быть разными: определение, кошка на изображении или собака, или определение качества вина на основе его кислотности и содержания алкоголя.

В зависимости от задачи классификации вы будете использовать разные типы классификаторов. Например, если классификация содержит какую-то бинарную логику, то к ней лучше всего подойдёт логистическая регрессия.

По мере накопления опыта вам будет проще выбирать подходящий тип классификатора. Однако хорошей практикой является реализация нескольких подходящих классификаторов и выбор наиболее оптимального и производительного.

Реализация классификатора

Первый шаг в реализации классификатора — его импорт в Python. Вот как это выглядит для логистической регрессии:

Вот импорты остальных классификаторов, рассмотренных выше:

Однако, это не все классификаторы, которые есть в Scikit-Learn. Про остальные можно прочитать на соответствующей странице в документации.

После этого нужно создать экземпляр классификатора. Сделать это можно создав переменную и вызвав функцию, связанную с классификатором.

Теперь классификатор нужно обучить. Перед этим нужно «подогнать» его под тренировочные данные.

Обучающие признаки и метки помещаются в классификатор через функцию fit :

Эти этапы (создание экземпляра, обучение и классификация) являются основными при работе с классификаторами в Scikit-Learn. Но эта библиотека может управлять не только классификаторами, но и самими данными. Чтобы разобраться в том, как данные и классификатор работают вместе над задачей классификации, нужно разобраться в процессах машинного обучения в целом.

Процесс машинного обучения

Процесс содержит в себе следующие этапы: подготовка данных, создание обучающих наборов, создание классификатора, обучение классификатора, составление прогнозов, оценка производительности классификатора и настройка параметров.

Во-первых, нужно подготовить набор данных для классификатора — преобразовать данные в корректную для классификации форму и обработать любые аномалии в этих данных. Отсутствие значений в данных либо любые другие отклонения — все их нужно обработать, иначе они могут негативно влиять на производительность классификатора. Этот этап называется предварительной обработкой данных (англ. data preprocessing).

Следующим шагом будет разделение данных на обучающие и тестовые наборы. Для этого в Scikit-Learn существует отличная функция traintestsplit.

Как уже было сказано выше, классификатор должен быть создан и обучен на тренировочном наборе данных. После этих шагов модель уже может делать прогнозы. Сравнивая показания классификатора с фактически известными данными, можно делать вывод о точности классификатора.

Вероятнее всего, вам нужно будет «корректировать» параметры классификатора, пока вы не достигните желаемой точности (т. к. маловероятно, что классификатор будет соответствовать всем вашим требованиям с первого же запуска).

Ниже будет представлен пример работы машинного обучения от обработки данных и до оценки.

Реализация образца классификации

Поскольку набор данных iris достаточно распространён, в Scikit-Learn он уже присутствует, достаточно лишь заложить эту команду:

Тем не менее, тут ещё нужно подгрузить CSV-файл, который можно скачать здесь.

Благодаря тому, что данные уже были подготовлены, долгой предварительной обработки они не требуют. Единственное, что может понадобиться — убрать ненужные столбцы (например ID ) таким образом:

Теперь нужно определить признаки и метки. С библиотекой Pandas можно легко «нарезать» таблицу и выбрать определённые строки/столбцы с помощью функции iloc() :

Код выше выбирает каждую строку и столбец, обрезав при этом последний столбец.

Выбрать признаки интересующего вас набора данных можно также передав в скобках заголовки столбцов:

После того, как вы выбрали нужные признаки и метки, их можно разделить на тренировочные и тестовые наборы, используя функцию train_test_split() :

Чтобы убедиться в правильности обработки данных, используйте:

Теперь можно создавать экземпляр классификатора, например метод опорных векторов и метод k-ближайших соседей:

Теперь нужно обучить эти два классификатора:

Эти команды обучили модели и теперь классификаторы могут делать прогнозы и сохранять результат в какую-либо переменную.

Теперь пришло время оценить точности классификатора. Существует несколько способов это сделать.

Нужно передать показания прогноза относительно фактически верных меток, значения которых были сохранены ранее.

Вот, к примеру, результат полученных метрик:

Поначалу кажется, что KNN работает точнее. Вот матрица неточностей для SVC:

Количество правильных прогнозов идёт с верхнего левого угла в нижний правый. Вот для сравнения метрики классификации для KNN:

Оценка классификатора

Когда дело доходит до оценки точности классификатора, есть несколько вариантов.

Точность классификации

Точность классификации измерять проще всего, и поэтому этот параметр чаще всего используется. Значение точности — это число правильных прогнозов, делённое на число всех прогнозов или, проще говоря, отношение правильных прогнозов ко всем.

Хоть этот показатель и может быстро дать вам явное представление о производительности классификатора, его лучше использовать, когда каждый класс имеет хотя бы примерно одинаковое количество примеров. Так как такое будет случаться редко, рекомендуется использовать другие показатели классификации.

Логарифмические потери

Значение Логарифмических Потерь (англ. Logarithmic Loss) — или просто логлосс — показывает, насколько классификатор «уверен» в своём прогнозе. Логлосс возвращает вероятность принадлежности объекта к тому или иному классу, суммируя их, чтобы дать общее представление об «уверенности» классификатора.

Этот показатель лежит в промежутке от 0 до 1 — «совсем не уверен» и «полностью уверен» соответственно. Логлосс сильно падает, когда классификатор сильно «уверен» в неправильном ответе.

Площадь ROC-кривой (AUC)

Такой показатель используется только при бинарной классификации. Площадь под ROC-кривой представляет способность классификатора различать подходящие и не подходящие какому-либо классу объекты.

Значение 1.0 : вся область, попадающая под кривую, представляет собой идеальный классификатор. Следовательно, 0.5 означает, что точность классификатора соответствует случайности. Кривая рассчитывается с учётом точности и специфичности модели. Подробнее о расчётах можно прочитать здесь.

Матрица неточностей

Матрица неточностей (англ. Confusion Matrix) — это таблица или диаграмма, показывающая точность прогнозирования классификатора в отношении двух и более классов. Прогнозы классификатора находятся на оси X, а результат (точность) — на оси Y.

Ячейки таблицы заполняются количеством прогнозов классификатора. Правильные прогнозы идут по диагонали от верхнего левого угла в нижний правый. Про это можно почитать в данной статье.

Отчёт о классификации

В библиотеке Scikit-Learn уже встроена возможность создавать отчёты о производительности классификатора. Эти отчёты дают интуитивно понятное представление о работе модели.

Заключение

Чтобы лучше вникнуть в работу с Scikit-Learn, неплохо было бы узнать больше о работе различных методов классификации. После этого стоит лучше узнать о замере производительности классификаторов. Однако понимание многих нюансов в классификации приходит только со временем.

Источник

9 ключевых алгоритмов машинного обучения простым языком

Машинное обучение (МО) уже меняет мир. Google использует МО предлагая и показывая ответы на поисковые запросы пользователей. Netflix использует его, чтобы рекомендовать вам фильмы на вечер. А Facebook использует его, чтобы предложить вам новых друзей, которых вы можете знать.

Машинное обучение никогда еще не было настолько важным и, в тоже время, настолько трудным для изучения. Эта область полна жаргонов, а количество разных алгоритмов МО растет с каждым годом.

Эта статья познакомит вас с фундаментальными концепциями в области машинного обучения. А конкретнее, мы обсудим основные концепции 9ти самых важных алгоритмов МО на сегодняшний день.

Система рекомендаций(Recommendation system)

Для построения полноценной системы рекомендаций с 0, требуются глубокие знания в линейной алгебре. Из-за чего, если вы никогда не изучали эту дисциплину, вам может быть сложно понять некоторые концепции этого раздела.

Но не беспокойтесь — scikit-learn библиотека Python позволяет довольно просто построить СР. Так что вам не потребуется таких уж глубоких познаний в линейной алгебре, чтобы построить рабочую СР.

Как работает СР?

Существует 2 основных типа система рекомендаций:

Коллаборативная фильтрация СР предоставляет рекоммендации, основанные на знаниях о том как пользователь взаимодействует с элементами(*примечание: за основу взяты взаимодействия с элементами других пользователей, схожих по поведению с данным пользователем). Другими словами, они используют «мудрость толпы»(отсюда и «коллаборативный» в названии метода).

В реальном мире коллаборативная фильтрация СР куда более распространена, нежели основанная на контенте система. Это обусловлено, преимущественно, потому что они обычно дают результат лучше. Некоторые специалист также находят коллаборативную систему более простой для понимания.

Коллаборативная фильтрация СР также обладает уникальной особенностью, которой нет в основанной на контенте ситстеме. А именно, у них есть способность обучаться фичам самостоятельно.

Это значит, что они могут даже начать определять подобие в элементах, основываясь на свойствах или чертах, которые вы даже не предоставляли для работы этой системе.

Существует 2 подкатегории коллаборативной фильтрации:

Подведем итог

Вот краткое резюме того, что мы узнали о системе рекомендаций в данной статье:

Линейная регрессия (Linear Regression)

Линейная регрессия используется для предсказаний некоторого значения y основываясь на некотором множестве значений x.

История линейной регрессии

Линейная регрессия(ЛР) была изобретена в 1800 году Френсисом Гальтоном. Гальтон был ученым, изучающим связь между родителями и детьми. А конкретнее, Гальтон исследовал связь между ростом отцов и ростом их сыновей. Первым открытием Гальтона стал тот факт, что рост сыновей, как правило, был приблизительно таким же как рост их отцов. Что не удивительно.

Позднее, Гальтон открыл нечто более интересное. Рост сына, как правило, был ближе к средне-общему росту всех людей, чем к росту его собственного отца.

Гальтон даль этому феномену название — регрессия. В частности, он сказал: » Рост сына имеет тенденцию к регрессии(или к смещению в направлении) среднего роста».

Это привело к целой области в статистике и машинном обучении под названием регрессия.

Математика линейной регрессии

В процессе создания регрессионной модели, все что мы пытаемся сделать — это нарисовать линию настолько близко к каждой точке из набора данных, на сколько это возможно.

Типичный пример такого подхода — «метод наименьших квадратов» линейной регрессии, с помощью которого рассчитывают близость линии в направлении верх-низ.

Пример для иллюстрации:

Когда вы создаете регрессионную модель, ваш конечный продукт — это уравнение, с помощью которого вы можете предсказать значения y для значения x без того чтобы знать значение y наперед.

Логистическая регрессия (Logistic Regression)

Логистическая регрессия схожа с линейной, за исключением того факта, что вместо вычисления значения у, она оценивает к какой категории принадлежит данная точка данных.

Что такое логистическая регрессия?

Логистическая регрессия — это модель машинного обучения, использующаяся для решения задач классификации.

Ниже представлено несколько примеров классификационных задач МО:

Логистическая регрессия хорошо подходит для решения задач двоичной классификации — мы просто назначаем разным категориям значения 0 и 1 соответственно.

Зачем нужна логистическая регрессия? Потому что вы не можете использовать линейную регрессию для прогнозов по двоичной классификации. Она просто не будет подходить, так как вы будете пытаться провести прямую линию через набор данных с двумя возможными значениями.

Это изображение может помочь понять почему линейная регрессия плохо подходит для двоичной классификации:

На этом изображении ось у представляет вероятность того, что опухоль является злокачественной. Значения 1-у представляет вероятность, что опухоль доброкачественная. Как вы можете видеть, модель линейной регрессии очень плохо срабатывает для предсказания вероятности для большинства наблюдений в наборе данных.

Вот почему логистическая регрессионная модель полезна. У нее есть изгиб к линии лучшего соответсвия, что делает ее(модель) гораздо более подходящей для предсказаний качественных(категорийных) данных.

Вот пример, который иллюстрирует сравнение линейной и логистической регрессионых моделей на одних и техже данных:

Сигмоида (The Sigmoid Function)

Причина по которой логистическая регрессия имеет изгиб — это тот факт, что для её вычисления не используетя линейное уравнение. Вместо него логистическая регерссионная модель строится на использовании сигмоиды (также называемой логистической функцией, т.к. она используется в логистической регрессии).

Для вас не обязательно досконально запоминать сигмоиду, чтобы преуспеть в МО. Но все-таки иметь некоторое представление об этой функции будет полезно.

Главная характеристика сигмоиды, которая стоит того, чтобы с ней разобраться — не важно какое значение вы передадите этой функции, она всегда вернет значение в промежутке 0-1.

Использование логистической регрессионной модели для предсказаний

Чтобы использовать логистическую регрессию для предсказаний, вам, как правило, нужно точно определить точку отсечения. Эта точка отсечения обычно 0.5.

Давайте использовать наш пример с диагностикой рака с предыдущего графика, чтобы увидеть этот принцип на практике. Если логистическая регрессионная модель выдаст значение ниже 0.5, то эта точка данных будет отнесена к категории доброкачественной опухоли. Подобным образом, если сигмоида выдаст значение выше 0.5, то опухоль отнесут к категории злокачественных.

Использование матрицы ошибок для измерения эффективности логистической регрессии

Матрица ошибок может быть использована в качестве инструмента для сравнения истинно положительных, истинно отрицательных, ложно положительных и ложно отрицательных показателей в МО.

Матрица ошибок, в частности, полезна, когда используется для измерения эффективности логистической регрессионной модели. Вот пример, как мы можем использовать матрицу ошибок:

В этой таблице TN означает «истинно отрицательно», FN — «ложно отрицательно», FP — «ложно положительно», TP — «истинно положительно».

Матрица ошибок полезна для оценки модели, есть ли в ней «слабые» квадранты в матрице ошибок. Как пример, она может иметь ненормально большое количество ложно положительных результатов.

Она также довольно полезна в некоторых случаях, для того чтобы убедиться, что ваша модель работает корректно в особенно опасной зоне матрицы ошибок.

В этом примере диагностики рака, например, вы бы хотели быть точно уверены, что у вашей модели не слишком большое количество ложно положительных результатов, т.к. это будет означать, что чью-то злокачественную опухоль вы диагностировали как доброкачественную.

Подведем итог

В этом разделе у вас было первое знакомство с моделью МО — логистической регрессией.
Вот краткое содержание того, что вы узнали о логистической регрессии:

Алгоритм k-ближайших соседей (K-Nearest Neighbors)

Алгоритм k-ближайших соседей может помочь решить задачу классификации, в случае, когда категорий больше, чем 2.

Что из себя представляет алгоритм k-ближайших соседей?

Это классификационный алгоритм, который базируется на простом принципе. На самом деле, принцип настолько прост, что лучше его продемонстрировать на примере.

Представьте, что у вас есть данные по высоте и весу футболистов и баскетболистов. Алгоритм k-ближайших соседей может быть использован для предсказания является ли новый игрок футболистом или баскетболистом. Чтобы это сделать, алгоритм определяет К точек данных, ближайших к объекту исследования.

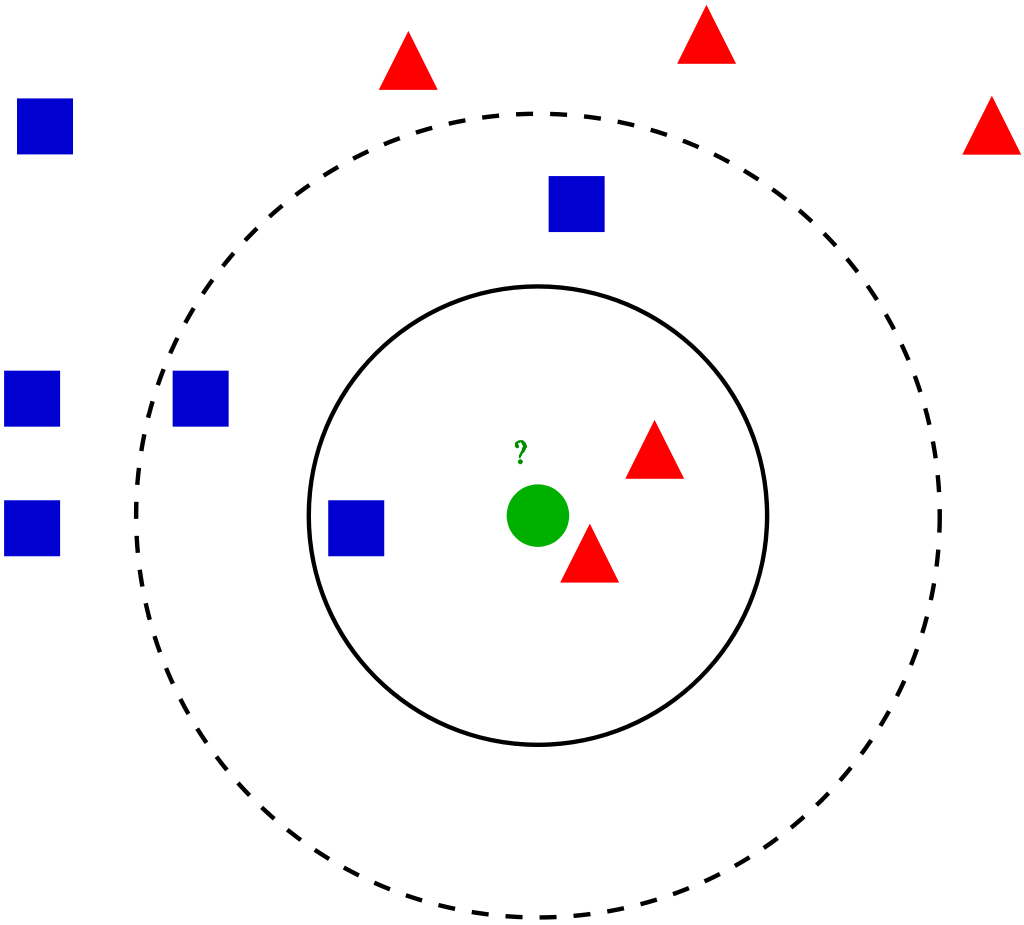
Данное изображение демонстрирует этот принцип с параметром К = 3:

На этом изображении футболисты изображены голубыми отметками, а баскетболисты — оранжевыми. Точка, которую мы пытаемся классифицировать, покрашена в зеленый цвет. Так как большинство (2 из 3) ближайших к зеленой точке отметок окрашены в голубой (футбольные игроки), то значит алгоритм К-ближайших соседей предсказывает, что новый игрок тоже окажется футболистом.

Как построить алгоритм К-ближайших соседей

Основные шаги для построения данного алгоритма:

Важность переменной К в алгоритме К-ближайших соседей

Хотя это может быть не очевидно с самого начала, изменение значения К в данном алгоритме изменит категорию, в которую попадет новая точка данных.

Конкретнее, слишком маленькое значение К приведет к тому, что ваша модель будет точно прогнозировать на обучающем множестве данных, но будет крайне не эффективна для тестовых данных. Также, имея слишком высокий К показатель, вы сделаете модель неоправданно сложной.

Представленная ниже иллюстрация отлично показывает этот эффект:

Плюсы и минусы алгоритма К-ближайших соседей

Чтобы подвести итог знакомства с этим алгоритмом, давайте коротко обсудим достоинства и недостатки его использования.

Подведем итог

Краткое содержание того, что вы только что узнали о алгоритме К-ближайших соседей:

Дерево решений и Случайный лес (Decision Trees and Random Forests)

Дерево решений и случайный лес — это 2 примера древовидного метода. Точнее, деревья решений — это модели МО, используемые для прогнозирования через циклический просмотр каждой функции в наборе данных один за одним. Случайный лес — это ансамбль (комитет) деревьев решения, которые используют случайные порядки объектов в наборе данных.

Что такое древовидный метод?

Перед тем, как мы нырнем в теоретические основы древовидного метода в МО, будет нелишним начать с примера.

Представьте, что вы играете в баскетбол каждый понедельник. Более того, вы всегда приглашаете одного и того же друга пойти поиграть с вами. Иногда друг действительно приходит, иногда нет. Решение приходить или нет зависит от множества факторов: какая погода, температура, ветер и усталость. Вы начинаете замечать эти особенности и отслеживать их вместе с решением вашего друга играть или нет.

Вы можете использовать эти данные для предсказания придет ли ваш друг сегодня или нет. Одна из техник, которой вы можете воспользоваться — это дерево решений. Вот как это выглядит:

У каждого дерева решений есть 2 типа элементов:

Вот еще парочка определений, которые вы должны понимать перед тем, как мы начнем:

Как построить дерево решений с нуля

Построение дерева решений сложнее, чем может показаться. Это происходит потому что решение на какие разветвления (характеристики) делить ваши данные (что является темой из области энтропии и получения данных) — это математически сложная задача.

Чтобы ее разрешить, специалисты МО обычно используют множество деревьев решения, применяя случайные наборы характеристик, выбранных для разделения дерева на них. Другими словами, новые случайные наборы характеристик выбираются для каждого отдельного дерева, на каждом отдельном разделении. Эта техника называется случайные леса.

В общем случае, специалисты обычно выбирают размер случайного набора характеристик (обозначается m) так, чтобы он был квадратным корнем общего количества характеристик в наборе данных (обозначается р). Если коротко, то m — это квадратный корень из р и тогда конкретная характеристика случайным образом выбирается из m.

Выгоды использования случайного леса

Представьте, что вы работаете с множеством данных, у которого есть одна «сильная» характеристика. Иными словами, в этом множестве данных есть характеристика, которая намного более предсказуема в отношении конечного результата, чем остальные характеристики этого множества.

Если вы строите дерево решений вручную, то имеет смысл использовать эту характеристку для самого «верхнего» разделения в вашем дереве. Это значит, что у вас будет несколько деревьев, прогнозы которых сильно коррелируют.

Мы хотим этого избежать, т.к. использование средней от сильно коррелирующих переменных не снижает значительно дисперсию. Используя случайные наборы характеристик для каждого дерева в случайном лесу, мы декоррелируем деревья и дисперсия полученной модели уменьшается. Эта декорреляция — главное преимущество в использовании случайных лесов в сравнении с деревьями решений, построенными вручную.

Подведем итог

Итак, краткое содержание того, что вы только что узнали о деревьях решений и случайных лесах:

Метод опорных векторов(Support Vector Machines)

Метод опорных векторов это алгоритм классификации (хотя, технически говоря, они также могут быть использованы для решения регрессионных задач), который делит множество данных на категории в местах наибольших «разрывов» между категориями. Эта концепция станет более понятной, если разобрать следующий пример.

Что такое метод опорных векторов?

Метод опорных векторов (МОВ) — это модель МО с учителем, с соответствующими алгоритмами обучения, которые анализируют данные и распознают закономерности. МОВ может быть использован как для задач классификации, так и для регрессионного анализа. В этой статье мы посмотрим конкретно на использование метода опорных векторов для решения задач классификации.

Как МОВ работает?

Давайте капнем поглубже в то, как действительно работает МОВ.

Нам дан набор тренировочных примеров, какждый из которого промаркирован как принадлежащий к одной из 2х категорий, и с помощью этого набора МОВ строит модель. Эта модель распределяет новые примеры в одну из двух категорий. Это делает МОВ невероятностным двоичным линейным классификатором.

МОВ использует геометрию для составления прогнозов по категориям. Конкретнее модель метода опорных векторов сопоставляет точки данных как точки в пространстве и разделяет на отдельные категории так, что они разделяются настолько широким разрывом, насколько возможно. Прогноз принадлежности новых точек данных к определенной категории основывается на том, с какой стороны разрыва находится точка.

Вот пример визуализации, который поможет вам понять интуицию МОВ:

Как вы можете наблюдать, если новая точка данных падает на левую от зеленой линии сторону, то она будет отнесена к «красным», а если на правую — то к «синим». Эта зеленая линия называется гиперплоскостью, и является важным термином для работы с МОВ.

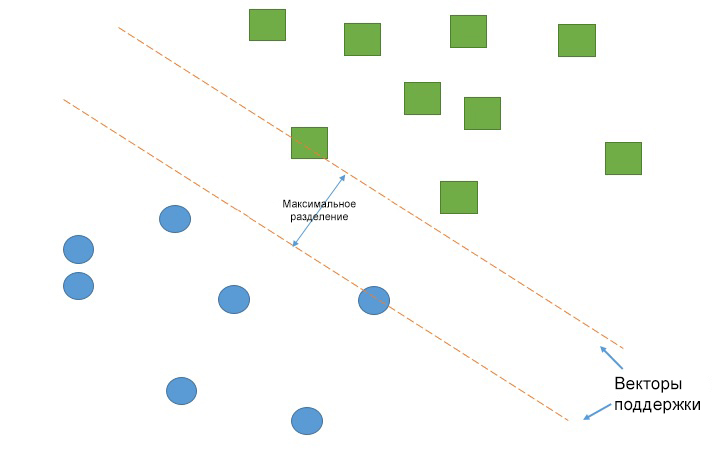
Давайте посмотрим следующее визуальное представление МОВ:

На этой диаграмме гиперплоскость обозначена как «оптимальная гиперплоскость» (optimal hyperplane). Теория метода опорных векторов дает такое определение оптимальной гиперплоскости — это гиперплоскость, которая максимизирует поле между двумя ближайшими точками данных из разных категорий.

Как вы видите, граница поля действительно затрагивает 3 точки данных — 2 из красной категории и 1 из синей. Эти точки, которые соприкасаются с границей поля, и называются опорными векторами — откуда и пошло название.

Подведем итог

Вот краткий очерк того, что вы только что узнали о методе опорных векторов:

Метод К-средних (K-Means Clustering)

Метод К-средних — это алгоритм машинного обучения без учителя. Это значит, что он принимает непомеченные данные и пытается сгруппировать кластеры подобных наблюдений ваших данных. Метод К-средних крайне полезен для решения реальных прикладных задач. Вот примеры нескольких задач, подходящих для этой модели:

Вот визуальное представление того, как это выглядит на практике:

Мы изучим математическую составляющую метода К-средних вследующем разделе этой статьи.

Как работает метод К-средних?

Первый шаг в работе метода К-средних — это выбор количества групп на которое вы хотите разделить ваши данные. Этим количеством и является значение К, отраженное в названии алгоритма. Выбор значения К в методе К-средних очень важен. Чуть позже мы обсудим как выбрать правильное значение К.

Далее, вы должны случайным образом выбрать точку в наборе данных и причислить ее к случайному кластеру. Это даст вам начальное положение данных, на котором вы прогоняете следующую итерацию до тех пор, пока кластеры перестанут изменяться:

Выбор подходящего значения К в методе К-средних

Строго говоря, выбор подходящего значения К — это довольно сложно. Не существует «правильного» ответа в выборе «лучшего» значения К. Один из методов, который специалисты по МО часто используют, называется «методом локтя».

Для использования этого метода, первое, что вам необходимо сделать, это вычислить сумму квадратов отклонений(sum of squared errors) — СКО для вашего алгоритма для группы значений К. СКО в методе К-средних определена как сумма квадратов расстояний между каждой точкой данных в кластере и центром тяжести этого кластера.

В качестве примера этого шага, вы можете вычислить СКО для значений К 2, 4, 6, 8 и 10. Далее вы захотите сгенерировать график СКО и этих значений К. Вы увидите, что отклонение уменьшается с увеличением значения К.

И это имеет смысл: чем больше категорий вы создадите на основе множества данных — тем более вероятно, что каждая точка данных окажется близко к центру кластера этой точки.
С учетом сказанного, основная идея метода локтя — это выбрать значение К при котором СКО резко замедлит темпы снижения. Это резкое снижение образует «локоть» на графике.

Как пример, вот график СКО относительно К. В этом случае, метод локтя предложит использовать значение К примерно равное 6.

Важно, что К=6 просто оценка приемлемого значения К. Не существует «лучшего» значения К в методе К-средних. Как и многие вещи в области МО, это очень зависящее от ситуации решение.

Подведем итог

Вот краткий очерк того, что вы только что узнали в этом разделе:

Метод главных компонент (Principal Component Analysis)

Метод главных компонент используется для преобразования набора данных c множеством параметров в новый набор данных с меньшим количеством параметров и каждый новый параметр этого набора данных — это линейная комбинация раннее существующих параметров. Эти преобразованные данные стремятся обосновать большую часть дисперсии оригинального набора данных с гораздо большей простотой.

Что такое метод главных компонентов?

Метод главных компонент (МГК) — это техника МО, которая используется для изучения взаимосвязей между наборами переменных. Другими словами, МГК изучает наборы переменных для того, чтобы определить базовую структуру этих переменных. МГК еще иногда называют факторным анализом.

На основании этого описания вы можете подумать, что МГК очень схож с линейной регрессией. Но это не так. На самом деле, эти 2 техники имеют несколько важных отличий.

Различия линейной регрессии и МГК

Линейная регрессия определяет линию наилучшего соответствия через набор данных. Метод главных компонентов определяет несколько ортогональных линий наилучшего соответствия для набора данных.

Если вы не знакомы с термином ортогональный, то это просто означает, что линии находятся под прямым углом друг к другу, как север, восток, юг и запад на карте.
Давайте рассмотрим пример, чтобы помочь вам понять это лучше.

Взгляните на метки осей на этом изображении. Главный компонент оси х объясняет 73% дисперсии в этом наборе данных. Главный компонент оси у объясняет около 23% дисперсии набора данных.

Это означает, что 4% дисперсии остается необъясненными. Вы можете уменьшить это число добавляя больше главных компонент в ваш анализ.

Подведем итог

Краткое содержание того, что вы только что узнали о методе главных компонент:

Источник