человек который быстро считает в уме
«Люди-счетчики» – невероятная способность суперсложных вычислений в уме
Совершая простейшие вычисления в уме, современные молодые люди делают ужасающие ошибки. Полагаясь только на калькуляторы и компьютеры, новое поколение катастрофически теряет способность к устному счету. Тем удивительнее, что в мире существуют феноменальные люди-счетчики, которые совершают в уме сложнейшие вычисления без применения каких-либо технических средств.
А вы умеете считать на счетах?
Некоторым современным молодым людям уже трудно представить время, когда не было компьютеров, а ведь, по историческим меркам, современная техника появилась в нашей стране совсем недавно. Я, например, в школе проходил вычисления с помощью арифмометра и логарифмической линейки, помню урок, когда мы даже считали на счетах. Как же в далекие времена люди умудрялись производить довольно сложные вычисления без использования компьютеров и калькуляторов?
Во-первых, те, кто был вынужден много считать, постоянно тренировались в этом и могли бы в устном счете заткнуть за пояс любого современного молодого человека. Во-вторых, в более сложных случаях они могли обратиться к дарованиям в области вычислений, молва о которых распространялась на большой территории. Так называемые люди-счетчики, способные в уме проводить очень сложные вычисления, появились еще в древние времена, однако о них сохранились только отрывочные упоминания. Первым феноменальным вычислителем, о котором существуют дошедшие до нас письменные свидетельства, был Джедедия Бакстон. Он родился в 1707 году в Элмтоне (графство Дербишир, Великобритания) в семье обычного деревенского учителя.
У мальчика оказался природный дар к вычислениям. Увы, уровень интеллекта у него был невысок, он не отличался ни честолюбием, ни склонностью хоть как-то использовать свой дар себе на пользу. Всю жизнь он трудился за гроши в качестве сельскохозяйственного рабочего, изредка получая небольшие суммы за демонстрацию своего дара любопытным приезжим. Стоит отметить, что Бакстон производил вычисления довольно медленно, пожалуй, главным его достижением можно назвать быстрое определение площади поля неправильной формы, для этого ему было достаточно лишь пройти по нему. Джедедия Бакстон скончался в возрасте 65 лет, так и не реализовав свой потенциал.
Как пастушок шокировал французских академиков
В отличие от Бакстона, французскому пастушку Анри Монде повезло гораздо больше. Пока коровы мирно паслись на лугу, Анри собирал маленькие кремни, располагал камешки рядами, представляя ими различные числа, а затем производил с ними вычисления. Со временем он настолько поднаторел в вычислениях, что практически мгновенно мог перевести возраст человека в число часов и даже минут.
Монде повезло, о его способностях узнал некий Якоби, который помог парню получить начальное школьное образование. Осенью 1840 года тот же Якоби представил молодое дарование ученым Французской академии наук. Когда Анри на заседании академии мгновенно вычислил квадрат 756 и правильно ответил на вопрос, сколько минут в 52 годах, ученые испытали одновременно и шок, и восторг. Монде назвали замечательным явлением и назначили для изучения феномена особую комиссию из пяти именитых академиков. Она дала очень положительное заключение о способностях юноши. Хотя сведения о дальнейшей судьбе Анри отсутствуют, скорее всего, она была более счастливой, чем у Бакстона.
Одним из уникальных людей-счетчиков был и англичанин Джордж Паркер Биддер, родившийся в 1806 году. Способности к счету и математике проявились у него еще в раннем возрасте, однако отец не хотел давать ему образование. К счастью, нашелся человек, по имени Джон Хершелл, оценивший способности мальчика, благодаря его помощи Биддер окончил начальную школу. Отец Джорджа, движимый жаждой наживы, пожелал забрать парнишку из школы и отдать его в цирк, чтобы зарабатывать на даре сына деньги. Однако у Бидцера появились защитники и покровители, давшие мальчику возможность закончить колледж.
За 6 минут Джордж Биддер мог умножить числа 257 689 435 на 356 875 649. Он обладал феноменальной памятью, например, мог запомнить сразу 43 числа, произнесенные всего раз. В 1834 году Биддер стал инженером-железнодорожником, выдающиеся способности Джорджа помогли Великобритании быстро обзавестись своей сетью железнодорожных путей. Биддер сыграл роль компьютера, которого тогда не было: с его помощью быстро и качественно было просчитано множество проектов. Когда 28 сентября 1878 года Биддер скончался, его уже посмертно признали одним из величайших людей-калькуляторов за историю человечества.
Вспомним еще об одном уникальном человеке-счетчике — уроженце Дании Виллеме Клейне (1912-1986). Он был занесен в Книгу рекордов Гиннесса благодаря своей способности извлечь корень 73-й степени из 500-значного числа. На этот процесс у него ушло всего 2 минуты и 43 секунды. В период 20—30-х годов прошлого века Клейн зарабатывал деньги, демонстрируя свои уникальные способности в цирке. В 1958 году он начал применять свой дар в Европейской организации по ядерным исследованиям, где проработал 19 лет. Потом, сославшись на усталость, Клейн покинул эту работу и перебрался в Амстердам. В отличие от Биддера, который умер своей смертью, Клейна 1 августа 1986 года в собственном доме зарезал неизвестный убийца.
Самые настоящие уникумы
Можете ли вы за 28 секунд в уме умножить два числа – 7 686 369 774 870 и 2 465 099 745 779 — и получить правильный ответ? Сомневаетесь? И правильно делаете. На такое способен лишь гениальный человек-счетчик. Если вдруг вы им являетесь, то вот вам правильный ответ — 18 947 668 177 995 426 462 773 730. Кстати, перемножила эти цифры за 28 секунд в 1980 году индианка Шакунтала Деви. Как видите, среди доминирующих в области суперсложных вычислений в уме мужчин иногда встречаются и женщины. В 38 лет Шакунтала могла, не пользуясь записями, извлечь корень 21-й степени из 210-значного числа. Проявился у нее и дар писателя, она опубликовала несколько книг.
На данный момент самым быстродействующим человеком-счетчиком на Земле считают Альберто Кото Гарсию. Он родился 20 мая 1970 года. Знаменитый «человек-компьютер», как его нередко называют, уже несколько лет подряд завоевывает первое место в мире в умножении и сложении в уме. Ему ничего не стоит умножить два восьмизначных числа, на это у него уходит 8 минут и 25 секунд. А вот сложить два стозначных числа Альберто может за 19,23 секунды.
Можно ли наладить «производство» супервычислителей?
Несомненно, выдающиеся люди-счетчики всегда представляли интерес для ученых, которые пытались узнать секрет их способностей. Еще в XIX веке в лаборатории физиологической психологии в Париже этим занимался Альфред Бине. Он не раскрыл сути феномена, но сделал ряд обобщений, касающихся людей-счетчиков. Бине установил отсутствие наследственности данного феномена, проявление способности к счету еще в детстве, ее развитие при постоянных упражнениях и угасание при отсутствии ее применения.
Люди-счетчики не делают секрета из того,как им удается справиться со сложнейшими вычислениями, однако их признания только еще больше озадачивают ученых. Урания Диамонди, например, рассказывала, что у каждой цифры есть свой цвет, а вычисления для нее — это игра бесконечных симфоний цвета. Одни люди-счетчики говорили, что кто-то словно выстраивает перед их глазами ряды цифр, другие рассказывали о каком-то постороннем вычислителе, проделывающем за них всю работу.
Пока ясно одно: в ближайшее время поставить на поток «производство» людей-счетчиков никому не удастся. Путем упорных тренировок можно достичь в устном счете немалых успехов, однако стать уникумом это не поможет.
Можно ли считать в уме и запоминать, как Дэниел Таммет
В статье «Интеллекутальные суперспособности» мы рассказывали о человеке с выдающимися умственными показателями – Дэниеле Таммете. Так вот в данной статье мы попробуем разобраться, можно ли запоминать и считать в уме так же, как он, не прибегая к помощи калькуляторов и другой вычислительной техники.
Кто такой Дэниел Таммет
Для начала немного о самом герое нашей статьи. Дэниел Таммет – это американский савант-вундеркинд, который может складывать, делить и умножать в уме числа, имеющие в своём составе до 100 знаков. Это даже не триллионы, а, наверное, те самые «гуголы» (числа с сотней нулей), о которых так любят говорить.
Родился Дэниел 31 января 1979 года в Лондоне. Свои способности проявил в возрасте 4 лет после сильнейшего приступа эпилепсии. В 2004 году побил мировой рекорд и воспроизвёл 22 514 знаков числа Пи после запятой.
Также этот человек знает 11 языков, включая родной для него английский. Изобрёл собственный язык (манти), грамматика которого напоминает финский и эстонский. Однако больше всего впечатляют, конечно, его математические способности.
Можно ли научиться быстро считать в уме большие числа
Если говорить коротко, то да, можно. Естественно, не точно так же, как это делает Дэниел, но всё равно достаточно хорошо. Для этого нужны лишь регулярные тренировки и руководство к действию.
Подобное руководство вы можете получить в нашем бесплатном курсе «Устный счёт». А здесь мы лишь кратко пройдёмся по основным его положениям.
Чтобы быстро считать в уме, нужно:
Ключевым является именно четвёртый пункт. Как говорится, теория без практики – это рюкзак с учебниками по плаванию за спиной тонущего.
Начать свои тренировки по развитию концентрации можно так:
Немного разобравшись с этим, можно переходить к математике. Вот десятка наиболее простых приемов, позволяющих быстро считать в уме сложные числа:
Таким образом, у вас уже есть несколько хороших приемов, чтобы лучше считать (узнать больше можно на нашем курсе «Устный счёт»). Но не будем ограничиваться счетом, а поговорим немного о запоминании.
Можно ли научиться запоминать большие числа
Как и на предыдущий вопрос, ответ на этот вопрос положительный. И учиться запоминать большие числа можно с нижеследующих простых приемов:
Однако чтобы информация прочно закреплялась в памяти, нужно не только правильно ее запоминать, но и грамотно повторять. Делать это нужно в соответствии с определённым графиком или режимом. Одним из самых эффективных режимов повторения является режим, предложенный доктором педагогических наук В. Ю. Васильевым.
Также очень эффективную схему повторения предложили американские учёные Хью Томпсон и Боб Салливан:
Считать в уме и запоминать огромные числа – это вполне достижимая цель. А чтобы узнать еще больше классных приемов запоминания, предлагаем познакомиться с нашей онлайн-программой «Мнемотехники». Всего за 5 недель с помощью специальных методик и онлайн-тренажёров вы научитесь быстро и надолго запоминать имена и лица, числа, даты, дни рождения, иностранные слова и многое другое.
Как быстро считать в уме: приемы устного счета больших чисел
Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.
Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.
После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).
Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.
Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.
Гаусс и устный счет

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.
По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.
В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.
Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.
Сложение чисел в уме
Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.
Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.
Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14
Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.
Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:
356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084
Вычитание чисел в уме
Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.
Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.
Теперь считаем: 528-300-20-1=228-20-1=208-1=207
Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.
Умножение чисел в уме
Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.
Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.
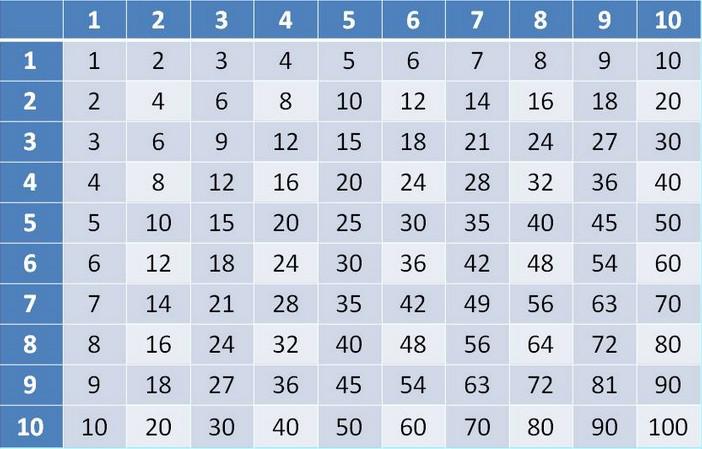
Умножение многозначных чисел на однозначные
Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.
528=500+20+8
528*6=500*6+20*6+8*6=3000+120+48=3168
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Умножение двузначных чисел
Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.
Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2
28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896
Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.
Умножение на 11
Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.
Проверим и умножим 54 на 11.
Возведение в квадрат
С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.
Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.
Проверим! Возведем в квадрат число 75.

Деление чисел в уме
Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.
Деление на однозначное число
При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.
Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:
6144:8=(5600+544):8=700+544:8
Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:
544:8=(480+64):8=60+64:8
Осталось разделить 64 на 8 и получить результат, сложив все результаты деления
6144:8=700+60+8=768
Деление на двузначное число
При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.
При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.
Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.
Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.
Сколько будет 4424:56?
Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.
56*80=4480
Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:
79*56=4424
Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Полезные советы
В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:
Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Эффективные способы быстрого счета в уме
Многие спрашивают, как научиться быстро считать в уме, чтобы это выглядело незаметно и неглупо. Ведь современные технологии позволяют меньше пользоваться своей памятью и умственными способностями. Но иногда нет под рукой данных технологий и порой легче и быстрее посчитать что-то в уме. Многие люди начали считать на калькуляторе или телефоне даже элементарные вещи, что также не очень хорошо. Умение считать в уме остается полезным навыком и для современного человека, несмотря на то, что он владеет всевозможными устройствами, способными считать за него. Возможность обходиться без специальных девайсов и в нужный момент оперативно решить поставленную арифметическую задачу – это не единственное применение данного навыка. Помимо утилитарного назначения, приемы устного счета позволят научиться организовывать себя в различных жизненных ситуациях. Кроме того, умение считать в уме, несомненно, положительно скажется на имидже ваших интеллектуальных способностей и выделит вас среди окружающих «гуманитариев».
Способы быстрого счета
Существует определенный набор простейших арифметических правил и закономерностей, которые не только нужно знать для устного счета, но и постоянно держать в голове, чтобы в нужный момент оперативно применить самый эффективный алгоритм. Для этого необходимо довести их использование до автоматизма, закрепить в машинальной памяти, чтобы от решения самых простых примеров успешно перейти к более сложным арифметическим действиям. Вот основные алгоритмы, которые нужно знать, помнить и применять мгновенно, автоматически:
Вычитание 7, 8, 9
Чтобы вычесть 9 из любого числа, нужно вычесть из него 10 и прибавить 1. Чтобы вычесть 8 из любого числа, нужно вычесть из него 10 и прибавить 2. Чтобы вычесть 7 из любого числа, нужно вычесть из него 10 и прибавить 3. Если обычно вы считаете по-другому, то для лучшего результата вам нужно привыкнуть к этому новому способу.
Умножение на 9
Быстро умножить любое число на 9 можно при помощи пальцев рук.
Деление и умножение на 4 и 8
Деление (или умножение) на 4 и на 8 являются двукратным или трехкратным делением (или умножением) на 2. Производить эти операции удобно последовательно.
Например, 46*4=46*2*2 =92*2= 184.
Умножение на 5
Умножать на 5 очень просто. Умножение на 5, и деление на 2 – это практически одно и то же. Так 88*5=440, а 88/2=44, поэтому всегда умножайте на 5, поделив число на 2 и умножив его на 10.
Умножение на 25
Умножение на 25 соответствует делению на 4 (с последующим умножением на 100). Так 120*25 = 120/4*100=30*100=3000.
Умножение на однозначные числа
Чтобы быстро считать в уме, полезно уметь умножать двузначные и трехзначные числа на однозначные. Для этого нужно умножать двух- или трехзначное число поразрядно.
Например, умножим 83*7.
Для этого сначала умножим 8 на 7 (и допишем ноль, так как 8 — разряд десятков), и прибавим к этому числу произведение 3 и 7. Таким образом, 83*7=80*7 +3*7= 560+21=581.
Возьмем более сложный пример: 236*3.
Итак, умножаем сложное число на 3 по разрядно: 200*3+30*3+6*3=600+90+18=708.
Определение диапазонов
Чтобы не запутаться в алгоритмах и по ошибке не выдать совсем неверный ответ, важно уметь строить примерный диапазон ответов. Так умножение однозначных чисел друг на друга может дать результат не более 90 (9*9=81), двузначных — не более 10 000 (99*99=9801), трехзначных не более — 1 000 000 (999*999=998001).
Раскладка на десятки и единицы
Способ заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.
63*85 = (60+3)*(80+5) = 60*80 + 60*5 +3*80 +3*5=4800+300+240+15=5355
Проще такие примеры решаются в 3 действия:
1. Сначала умножаются десятки друг на друга.
2. Потом складываются 2 произведения единиц на десятки.
3. Затем прибавляется произведение единиц.
Схематично это можно описать так:
— Первое действие: 60*80 = 4800 — запоминаем
— Второе действие: 60*5+3*80 = 540 – запоминаем
— Третье действие: (4800+540)+3*5= 5355 – ответ
Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.
Мысленная визуализация умножения в столбик
56*67 – посчитаем в столбик. Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа.
Но его можно упростить:
Первое действие: 56*7 = 350+42=392
Второе действие: 56*6=300+36=336 (ну или 392-56)
Третье действие: 336*10+392=3360+392=3 752
Частные методики умножения двузначных чисел до 30
Преимуществом трех способов умножения двузначных для устного счета состоит в том, что они универсальны для любых чисел и при хорошем навыке устного счета, они могут позволить вам достаточно быстро прийти к правильному ответу. Однако эффективность умножения некоторых двузначных чисел в уме может быть выше за счет меньшего количества действий при использовании специальных алгоритмов.
Умножение на 11
Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры.
Например: 23*11, пишем 2 и 3, а между ними ставим сумму (2+3). Или короче, что 23*11= 2 (2+3) 3 = 253.
Если сумма чисел в центре дает результат больше 10, тогда добавляем единицу к первой цифре, а вместо второй цифры пишем сумму цифр умножаемого числа минус 10.
Например: 29*11 = 2 (2+9) 9 = 2 (11) 9 = 319.
Быстро умножать на 11 устно можно не только двузначные числа, но и любые другие числа.
Например: 324 * 11=3(3+2)(2+4)4=3564
Квадрат суммы, квадрат разности
Для того чтобы возвести в квадрат двузначное число, можно воспользоваться формулами квадрата суммы или квадрата разности. Например:
23²= (20+3)2 = 202 + 2*3*20 + 32 = 400+120+9 = 529
69² = (70-1)2 = 702 – 70*2*1 + 12 = 4 900-140+1 = 4 761
Возведение в квадрат чисел, заканчивающихся на 5.Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу дописываем 25.
25² = (2*(2+1)) 25 = 625
85² = (8*(8+1)) 25 = 7 225
Это верно и для более сложных примеров:
155² = (15*(15+1)) 25 = (15*16)25 = 24 025
Методика умножения чисел до 20 очень проста:
16*18 = (16+8)*10+6*8 = 288
Опорное число
Посмотрите на суть этого метода на примере умножения 15 и 18. Здесь удобно использовать опорное число 10. 15 больше десяти на 5, а 18 больше десяти на 8.
Для того, чтобы узнать их произведение, нужно совершить следующие операции:
15*18
1. К любому из множителей прибавить число, на которое второй множитель больше опорного. То есть прибавить 8 к 15, или 5 к 18. В первом и втором случае получается одно и то же: 23.
2. Затем 23 умножаем на опорное число, то есть на 10. Ответ: 230
3. К 230 прибавляем произведение 5*8. Ответ: 270.
Опорное число при умножении чисел до 100.Наиболее популярной методикой умножения больших чисел в уме является прием использования, так называемого, опорного числа
Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. При умножении чисел до 100 опорными числами удобно использовать все числа кратные 10, а особенно 10, 20, 50 и 100.
Методика использования опорного числа зависит от того, являются ли множители больше или меньше опорного числа. Тут возможны три случая. Покажем, все 3 методики на примерах.
Оба числа меньше опорного (под опорным). Допустим, мы хотим умножить 48 на 47.
Эти числа находятся достаточно близко к числу 50, а следовательно удобно использовать 50 в качестве опорного числа.
Чтобы умножить 48 на 47, используя опорное число 50, нужно:
47*48
1. Из 47 вычесть столько, сколько не хватает 48 до 50, то есть 2. Получается 45 (или
из 48 вычесть 3 – это всегда одно и то же)
2. Дальше 45 умножаем на 50 = 2250
3. Затем прибавляем 2*3 к этому результату – 2 256
Одно число под опорным, а другое над.Третий случай использования опорного числа – когда одно число больше опорного, а другое меньше. Такие примеры решаются не сложнее, чем предыдущие. Меньший множитель увеличиваем на разность между вторым множителем и опорным числом, результат умножаем на опорное число и вычитаем произведение разностей опорного числа и множителей. Или больший множитель уменьшаем на разность между вторым множителем и опорным числом, результат умножаем на опорное число и вычитаем произведение разностей опорного числа и множителей.
(52-5)*50-5*2=47*50-10=2340 или (45+2)*50-5*2=47*50-10=2340
27*89
Таким образом, с помощью использования одного опорного числа можно умножать большую комбинацию двузначных чисел. Описанные выше методики можно разделить на универсальные (подходящие для любых чисел) и частные (удобные для конкретных случаев).
В крайнем случае, можно воспользоваться «крестьянским» счетом. Чтобы умножить одно число на другое, допустим 21*75, нам нужно записать числа в две колонки. Первое число левой колонки 21, первое число правого столбика 75. Затем числа стоящие в левой колонке делить на 2 и отбрасывать остаток, пока не получим единицу, а числа в правой колонке умножаем на 2. Все строчки, имеющие четные числа в левой колонке вычеркиваем, а оставшиеся числа в правой колонке складываем, у нас получается точный результат.
21*75
Чтобы научиться быстро считать в уме, нужна практика, нет волшебных методик, чтобы с первого раза начать быстро считать в голове, необходимо постоянно тренировать свой мозг и заставлять его быстро работать и считать.
Заключение
Как и все способы вычислений, данные методы быстрого счета имеют свои достоинства и недостатки:
ПЛЮСЫ:
1.С помощью различных методов быстрых вычислений даже самый малообразованный человек может считать.
2. Способы быстрого счета могут помочь избавиться от сложного действия, путем замены его на несколько более простых.
3.Способы быстрого счета полезны в ситуациях, когда нельзя воспользоваться умножением в столбик.
4.Способы быстрого счета позволяют сократить время вычислений.
5.Устный счет развивает умственную деятельность, что помогает быстрее ориентироваться в сложных жизненных ситуациях.
6. Техника устного счета делает процесс вычислений более увлекательным и интересным.
МИНУСЫ:
Несомненно, практика играет важнейшую роль в развитии любых способностей. Но навык устного счета не опирается на один лишь опыт. Это доказывают люди, которые способны считать в уме сложные примеры. Например, такие люди могут умножать и делить трехзначные числа, совершать арифметические операции, которые не каждый человек и в столбик сможет посчитать. Что же необходимо знать и уметь обычному человеку, чтобы овладеть такой феноменальной способностью? На сегодняшний день существуют различные методики, помогающие научиться быстро считать в уме.
Изучив многие подходы к обучению навыку считать устно, можно выделить 3 основных составляющих данного навыка:
1. Способности. Способность концентрировать внимание и умение удерживать в краткосрочной памяти несколько вещей одновременно. Предрасположенность к математике и логическому мышлению.
2. Алгоритмы. Знание специальных алгоритмов и умение оперативно подобрать нужный, максимально эффективный алгоритм в каждой конкретной ситуации.
3. Тренировка и опыт, значение которых для любого навыка никто не отменял. Постоянные тренировки и постепенное усложнение решаемых задач и упражнения позволят вам улучшить скорость и качество устного счета. Нужно отметить, что третий фактор имеет ключевое значение. Не обладая необходимым опытом, вы не сможете удивить окружающих быстрым счетом, даже если вы знаете самый удобный алгоритм. Однако не стоит недооценивать важность первых двух составляющих, поскольку имея в своем арсенале способности и набор нужных алгоритмов, вы сможете удивить даже самого опытного «счетовода», при условии, что вы тренировались одинаковое время.


