k means машинное обучение
Кластеризация: алгоритмы k-means и c-means
Как и обещал, продолжаю серию публикаций о технологии Data Mining. Сегодня хочу рассказать о двух алгоритмах кластеризации (k-means и c-means), описать преимущества и недостатки, дать некоторые рекомендации по их использованию. Итак, поехали…
Кластеризация — это разделение множества входных векторов на группы (кластеры) по степени «схожести» друг на друга.
Кластеризация в Data Mining приобретает ценность тогда, когда она выступает одним из этапов анализа данных, построения законченного аналитического решения. Аналитику часто легче выделить группы схожих объектов, изучить их особенности и построить для каждой группы отдельную модель, чем создавать одну общую модель для всех данных. Таким приемом постоянно пользуются в маркетинге, выделяя группы клиентов, покупателей, товаров и разрабатывая для каждой из них отдельную стратегию (Википедия).
Меры расстояний
Для того, чтобы сравнивать два объекта, необходимо иметь критерий, на основании которого будет происходить сравнение. Как правило, таким критерием является расстояние между объектами.
Есть множество мер расстояния, рассмотрим несколько из них:
Евклидово расстояние — наиболее распространенное расстояние. Оно является геометрическим расстоянием в многомерном пространстве.
Квадрат евклидова расстояния. Иногда может возникнуть желание возвести в квадрат стандартное евклидово расстояние, чтобы придать большие веса более отдаленным друг от друга объектам.
Расстояние городских кварталов (манхэттенское расстояние). Это расстояние является просто средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако отметим, что для этой меры влияние отдельных больших разностей (выбросов) уменьшается (так как они не возводятся в квадрат).
Расстояние Чебышева. Это расстояние может оказаться полезным, когда желают определить два объекта как «различные», если они различаются по какой-либо одной координате (каким-либо одним измерением).
Степенное расстояние. Иногда желают прогрессивно увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Это может быть достигнуто с использованием степенного расстояния.
Выбор расстояния (критерия схожести) лежит полностью на исследователе. При выборе различных мер результаты кластеризации могут существенно отличаться.
Алгоритм k-means (k-средних)
Наиболее простой, но в то же время достаточно неточный метод кластеризации в классической реализации. Он разбивает множество элементов векторного пространства на заранее известное число кластеров k. Действие алгоритма таково, что он стремится минимизировать среднеквадратичное отклонение на точках каждого кластера. Основная идея заключается в том, что на каждой итерации перевычисляется центр масс для каждого кластера, полученного на предыдущем шаге, затем векторы разбиваются на кластеры вновь в соответствии с тем, какой из новых центров оказался ближе по выбранной метрике. Алгоритм завершается, когда на какой-то итерации не происходит изменения кластеров.
Проблемы алгоритма k-means:
* необходимо заранее знать количество кластеров. Мной было предложено метод определения количества кластеров, который основывался на нахождении кластеров, распределенных по некоему закону (в моем случае все сводилось к нормальному закону). После этого выполнялся классический алгоритм k-means, который давал более точные результаты.
* алгоритм очень чувствителен к выбору начальных центров кластеров. Классический вариант подразумевает случайный выбор класторов, что очень часто являлось источником погрешности. Как вариант решения, необходимо проводить исследования объекта для более точного определения центров начальных кластеров. В моем случае на начальном этапе предлагается принимать в качестве центов самые отдаленные точки кластеров.
* не справляется с задачей, когда объект принадлежит к разным кластерам в равной степени или не принадлежит ни одному.
Нечеткий алгоритм кластеризации с-means
С последней проблемой k-means успешно справляется алгоритм с-means. Вместо однозначного ответа на вопрос к какому кластеру относится объект, он определяет вероятность того, что объект принадлежит к тому или иному кластеру. Таким образом, утверждение «объект А принадлежит к кластеру 1 с вероятностью 90%, к кластеру 2 — 10% » верно и более удобно.
Классический пример с-means — т.н. «бабочка» (butterfly):
Как видно, точка с координатами (3,2) в равной степени принадлежит как первому так и второму кластеру.
Остальные проблемы у с-means такие же, как у k-means, но они нивелируются благодаря нечеткости разбиения.
Модуль: кластеризация методом k-средних
В этой статье описывается, как использовать модуль кластеризации методом k-средних в конструкторе Машинного обучения Azure для создания необученной модели кластеризации методом k-средних.
K-средние — это один из самых простых и известных неконтролируемых алгоритмов обучения. Его можно использовать для различных задач машинного обучения, таких как:
Чтобы создать модель кластеризации, выполните следующие действия.
После настройки гиперпараметров модуля необученная модель подключается к обучающей модели кластеризации. Поскольку алгоритм k-средних является неконтролируемым методом обучения, столбец меток необязателен.
Если данные содержат метку, значения меток можно использовать как ориентир при выборе кластеров и оптимизации модели.
Если данные не имеют меток, алгоритм создает кластеры, представляющие возможные категории, основываясь исключительно на данных.
Общие сведения о кластеризации методом k-средних
Как правило, при кластеризации используются приемы итерации, позволяющие сгруппировать варианты из набора данных в кластеры со схожими характеристиками. Такие группировки полезно использовать для изучения данных, выявления в них аномалий и создания прогнозов. Модели кластеризации также могут помочь выявить связи в наборе данных, которые нельзя вывести логически путем просмотра или простого наблюдения. По этим причинам кластеризация часто используется на ранних этапах задач машинного обучения для изучения данных и выявления необычных корреляций.
При настройке модели кластеризации с помощью метода k-средних необходимо указать целевое число k, которое указывает количество центроидов в модели. Центроид — это репрезентативная точка в каждом кластере. Алгоритм k-средних назначает каждую входящую точку данных одному из кластеров за счет уменьшения суммы квадратов в кластере.
При обработке обучающих данных алгоритм k-средних начинает работу с начального набора случайно выбранных центроидов. Центроиды служат отправными точками для кластеров и применяют алгоритм Ллойда для итеративного уточнения своих расположений. Алгоритм k-средних прекращает построение и уточнение кластеров, когда выполняется одно из указанных ниже условий.
Центроиды стабилизируются. Это означает, что назначение кластеров отдельным точкам больше не меняется, то есть алгоритм пришел к решению.
Алгоритм выполнил указанное число итераций.
После завершения обучения используйте модуль назначения данных в кластеры, чтобы назначить новые варианты одному из кластеров, найденных с помощью алгоритма k-средних. Кластер назначается путем вычисления расстояния между новым вариантом и центроидом каждого кластера. Каждый новый вариант назначается кластеру с ближайшим центроидом.
Настройка модуля кластеризации методом k-средних
Добавьте модуль кластеризации методом k-средних в конвейер.
Чтобы указать, как обучать модель, выберите команду Создать режим преподавателя.
В поле Число центроидов укажите число кластеров, с которых алгоритм должен начинать свою работу.
Нет гарантий, что в модели будет ровно столько кластеров. Алгоритм начинается с этого количества точек данных и выполняет итерации для поиска оптимальной конфигурации. Можно обратиться к исходному коду sklearn.
Инициализация свойств позволяет указать алгоритм для определения первоначальной конфигурации кластера.
Первые N. Из набора данных выбирается некоторое начальное количество точек данных, которые используются в качестве исходных средних.
Этот метод также называется методом Форджи.
Случайный выбор. Этот алгоритм случайным образом помещает точку данных в кластер, а затем вычисляет исходное среднее для определения центроида случайно назначенных кластеру точек.
Этот метод также называется методом случайного разбиения.
K-средние++. Это метод по умолчанию для инициализации кластеров.
Алгоритм k-средних++ был предложен в 2007 году Дэвидом Артуром и Сергеем Васильвицким как решение проблемы неэффективной кластеризации при использовании стандартного метода k-средних. Метод k-средних++ — это улучшенный вариант стандартного метода k-средних, использующий другой метод для выбора исходных центров кластеров.
В поле случайного начального значения при необходимости введите значение, которое будет использоваться как начальное для инициализации кластера. Это значение может существенно повлиять на выбор кластера.
В поле Метрика выберите функцию, используемую для измерения расстояния между векторами кластера или между новыми точками данных и случайным образом выбранным центроидом. Машинное обучение Azure поддерживает следующие метрики расстояний кластера:
Для итераций укажите, сколько раз алгоритм должен пройти по обучающим данным перед тем, как завершит выбор центроидов.
Этот параметр можно настроить, чтобы сбалансировать точность и время обучения.
В качестве режима назначения метки выберите параметр, указывающий, как должен обрабатываться столбец меток, если он есть в наборе данных.
Поскольку кластеризация методом k-средних — это неконтролируемый метод машинного обучения, метки необязательны. Но если в наборе данных уже есть столбец меток, эти значения можно использовать для выбора кластеров, или можно указать, что значения следует игнорировать.
Пропустить столбец меток. Значения в столбце меток игнорируются и не используются при построении модели.
Заполнение отсутствующих значений. Значения столбца меток используются в качестве компонентов для создания кластеров. Если в строках отсутствует метка, значение определяется с помощью других компонентов.
Перезаписывать данные из ближайшей к центру. Значения столбца меток заменяются прогнозируемыми значениями меток, причем для этого используется метка точки, ближайшей к текущему центроиду.
Выберите параметр Нормализация компонентов, если требуется нормализовать компоненты перед обучением.
При использовании нормализации до начала обучения точки данных нормализуются в [0,1] с помощью MinMaxNormalizer.
Результаты
После завершения настройки и обучения вы получите модель, которую можно использовать для создания оценок. Однако существует несколько способов обучения модели, а также несколько способов просмотра и использования результатов.
Запись моментального снимка модели в рабочей области
Если вы использовали модуль обучающей модели кластеризации, выполните следующие действия.
Выберите модуль обучающей модели кластеризации и откройте панель справа.
Перейдите на вкладку Выходные данные. Щелкните значок Регистрация набора данных, чтобы сохранить копию обученной модели.
Сохраненная модель представляет обучающие данные на момент ее сохранения. Если впоследствии вы обновите обучающие данные, используемые в конвейере, сохраненная модель не обновится.
Просмотр результирующего набора данных кластеризации
Если вы использовали модуль обучающей модели кластеризации, выполните следующие действия.
Щелкните правой кнопкой мыши модуль обучающей модели кластеризации.
Выберите Визуализировать.
Советы по созданию лучшей модели кластеризации
Известно, что процесс присвоения начальных значений, используемый во время кластеризации, может значительно повлиять на модель. Присвоение начальных значений — это начальное размещение точек в потенциальных центроидах.
Например, если набор данных содержит много выбросов и для начального заполнения кластеров выбираются выбросы, другие точки данных будут плохо подходить этому кластеру, и кластер может быть одноэлементным. То есть у него может быть только одна точка.
Эту проблему можно решить двумя способами:
Изменить количество центроидов и попробовать несколько начальных значений.
Создать несколько моделей, изменяя метрику или выполняя больше итераций.
Как правило, при использовании моделей кластеризации возможна ситуация, когда любая заданная конфигурация приведет к созданию локально оптимизированного набора кластеров. Иными словами, набор кластеров, возвращаемых моделью, подходит только к текущим точкам данных и не является обобщенным для других данных. При использовании другой исходной конфигурации метод k-средних может дать более оптимальный результат.
Дальнейшие действия
Ознакомьтесь с набором доступных модулей в службе Машинного обучения Azure.
Дата публикации Jun 9, 2018
K-средства псевдокод
Моделирование ниже обеспечит лучшее понимание алгоритма K-средних.
Из приведенного выше графика можно сделать вывод, что при k = 4 график достигает оптимального минимального значения. Даже если расстояние внутри кластера уменьшается после 4, мы будем делать больше вычислений. Что просто аналогично закону убывающей отдачи. Поэтому мы выбираем значение 4 в качестве оптимального количества кластеров. Причина, по которой он назван методом локтя, заключается в том, что оптимальное количество кластеров будет представлять локтевой сустав!
Применение алгоритма кластеризации K-средних
Есть только несколько примеров, где применяется алгоритм кластеризации, такой как K-means.
Давайте напишем некоторый код
Мы будем использоватьНабор данных Irisпостроить наш алгоритм. Хотя в наборе данных Iris есть метки, мы будем отбрасывать их и будем использовать только характерные точки для кластеризации данных. Мы знаем, что существует 3 кластера («Iris-virginica», «Iris-setosa», «Iris-versicolor»). Следовательно, k = 3 в нашем случае.
Мы загружаем набор данных и сбрасываем целевые значения. Мы конвертируем характерные точки в простой массив и разбиваем его на данные обучения и тестирования.
Мы реализуем псевдокод, показанный выше, и мы можем обнаружить, что наш алгоритм сходится после 6 итераций. Теперь мы можем ввести тестовую точку данных и найти центроид, к которому она ближе всего, и назначить эту точку соответствующему кластеру.
Библиотека Scikit-learn снова избавляет нас от написания столь большого количества строк кода, предоставляя объект абстрактного уровня, который мы можем просто использовать для реализации алгоритма.
Вывод
Алгоритм k средних (k-means)
| Алгоритм [math]k[/math] средних (k-means) | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(ikdn)[/math] |
| Объём входных данных | [math] dn [/math] |
| Объём выходных данных | [math] n [/math] |
Содержание
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Цель алгоритма заключается в разделении [math]n[/math] наблюдений на [math]k[/math] кластеров таким образом, чтобы каждое наблюдение принадлежало ровно одному кластеру, расположенному на наименьшем расстоянии от наблюдения.
1.2 Математическое описание алгоритма
| [math]\arg\min_ | [math](1)[/math] |
где [math]\mathbf<\mu>_i[/math] – центры кластеров, [math]i=1. k, \quad \rho(\mathbf
Выбирается произвольное множество точек [math]\mu_i, \ i=1. k,[/math] рассматриваемых как начальные центры кластеров: [math]\mu_i^ <(0)>= \mu_i, \quad i=1. k[/math]
Шаг [math]t: \forall \mathbf
Шаг [math]t: \forall i=1. k: \mu_i^ <(t)>= \cfrac<1><|S_i|>\sum_<\mathbf
1.3 Вычислительное ядро алгоритма
Вычислительным ядром являются шаги 2 и 3 приведенного выше алгоритма: распределение векторов по кластерам и пересчет центров кластеров.
Пересчет центров кластеров предполагает [math]k[/math] вычислений центров масс [math]\mathbf<\mu>_i[/math] множеств [math]S_i, \ i=1. k,[/math] представленных выражением в шаге 3 представленного выше алгоритма.
1.4 Макроструктура алгоритма
Наиболее распространенными являются следующие стратегии:
Распределение векторов по кластерам
Для этого шага алгоритма между векторами [math]\mathbf
| [math] \mathbf | [math](2)[/math] |
Пересчет центров кластеров
Для этого шага алгоритма производится пересчет центров кластера по формуле вычисления центра масс:
| [math] \mu = \cfrac<1><|S|>\sum_<\mathbf | [math](3)[/math] |
1.5 Схема реализации последовательного алгоритма
1. Инициализировать центры кластеров [math]\mathbf<\mu>_i^<(1)>, \ i=1. k[/math]
2. [math]t \leftarrow 1[/math]
3. Распределение по кластерам
[math]\quad S_i^<(t)>=\<\mathbf
[math]\quad[/math] где каждый вектор [math]\mathbf
4. Обновление центров кластеров
[math]\quad \mathbf<\mu>_i^ <(t+1)>= \frac<1><|S^<(t)>_i|> \sum_<\mathbf
5. if [math]\exists i \in \overline<1,k>: \mathbf<\mu>_i^ <(t+1)>\ne \mathbf<\mu>_i^<(t)>[/math] then
[math]\quad t = t + 1[/math] ;
[math]\quad[/math] goto 3;
[math]
1.6 Последовательная сложность алгоритма
Аналогично [math]\Theta_<\rm distance>^d[/math] – временная сложность вычисления расстояния между двумя d-мерными векторами.
Сложность шага инициализации [math]k[/math] кластеров мощности [math]m[/math] в d-мерном пространстве – [math]\Theta_<\rm init>^
Cложность шага распределения d мерных векторов по [math]k[/math] кластерам – [math]\Theta_<\rm distribute>^
Сложность шага пересчета центров [math]k[/math] кластеров размера [math]m[/math] в d-мерном пространстве – [math]\Theta_<\rm recenter>^
Рассчитаем [math]\Theta_<\rm centroid>^
[math]\Theta_<\rm centroid>^
Рассчитаем [math]\Theta_<\rm distance>^d[/math] в соответствие с формулой [math](2)[/math]
[math]\Theta_<\rm distance>^d[/math] = [math]d[/math] вычитаний + [math]d[/math] умножений + [math](d-1)[/math] сложение
Предположим, что алгоритм сошелся за [math]i[/math] итераций, тогда временная сложность алгоритма [math]\Theta_<\rm k-means>^
[math]\Theta_<\rm k-means>^
[math]\Theta_<\rm k-means>^
Получаем, что временная сложность алгоритма k-means кластеризации [math]n[/math] d-мерных векторов на [math]k[/math] кластеров за [math]i[/math] итераций:
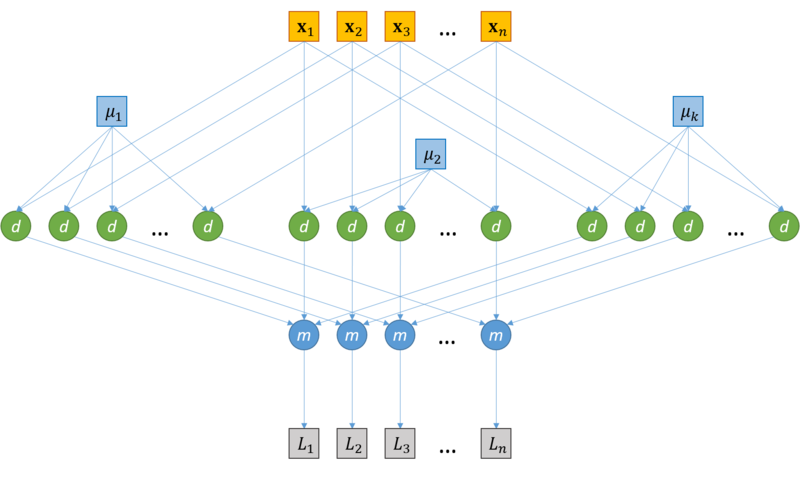
1.7 Информационный граф
Рассмотрим информационный граф алгоритма. Алгоритм k-means начинается с этапа инициализации, после которого следуют итерации, на каждой из которых выполняется два последовательных шага (см. «Схема реализации последовательного алгоритма»):
Поскольку основная часть вычислений приходится на шаги итераций, распишем информационные графы данных шагов.
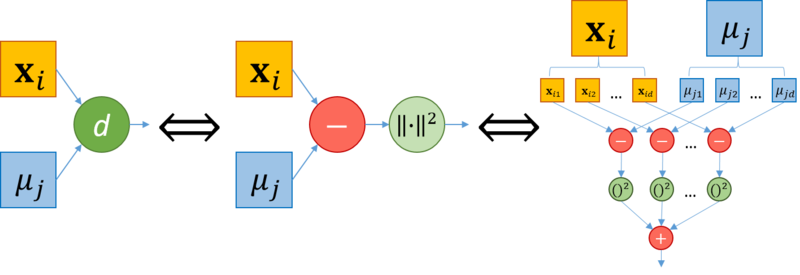
Распределение векторов по кластерам
Вычисление расстояния между векторами
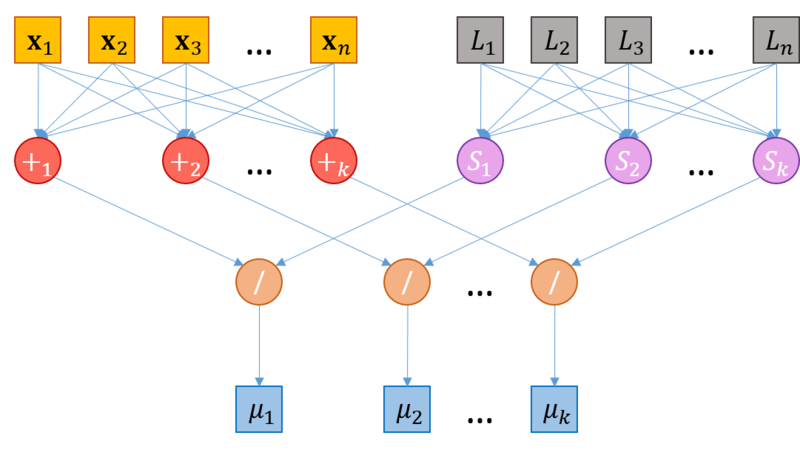
Пересчет центров кластеров
1.8 Ресурс параллелизма алгоритма
Пересчет центров кластеров в d-мерном пространстве
Общая параллельная сложность алгоритма
1.9 Входные и выходные данные алгоритма
Объем входных данных
[math]1[/math] целое число + [math]n \cdot d[/math] вещественных чисел (при условии, что координаты – вещественные числа).
Объем выходных данных
[math]n[/math] целых положительных чисел.
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности алгоритма
Сильные стороны алгоритма:
Чувствительность к начальным условиям
Инициализация центров кластеров в значительной степени влияет на результат кластеризации.
Чувствительность к выбросам и шумам
Выбросы, далекие от центров настоящих кластеров, все равно учитываются при вычислении их центров.
Возможность сходимости к локальному оптимуму
Итеративный подход не дает гарантии сходимости к оптимальному решению.
Использование понятия «среднего»
Алгоритм неприменим к данным, для которых не определено понятие «среднего», например, категориальным данным.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.1.1 Структура обращений в память и качественная оценка локальности
2.2.1.2 Количественная оценка локальности
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
В настоящем разделе проведено исследование масштабируемости различных параллельных реализации алгоритма [math]k[/math] средних согласно методике AlgoWiki.
2.4.1 Реализация 1
Параметры запусков для экспериментальной оценки:
Для проведения экспериментов были сгенерированы нормально распределенные псевдослучайные данные (с использованием Python библиотеки scikit-learn):
Для заданной конфигурации эксперимента ( [math]n, d, p, k[/math] ) и полученных результатов ( [math]t, i[/math] ) производительность и эффективность реализации расчитывались по формулам:
где [math]N_<\rm k-means>^
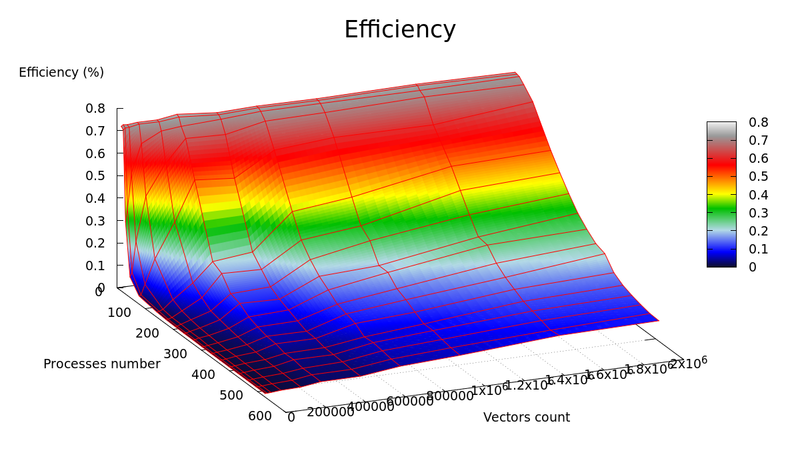
Графики зависимости производительности и эффективности параллельной реализации k-means от числа векторов для кластеризации ( [math]n[/math] ) и числа процессоров ( [math]p[/math] ) представлены на рисунках 4 и 5, соответственно.
В результате экспериментальной оценки были получены следующие оценки эффективности реализации:
Оценки масштабируемости реализации алгоритма k-means:
2.4.2 Реализация 2
Исследование также проводилось на суперкомпьютере «Ломоносов».
Набор данных для тестирования состоял из 946000 векторов размерности 2 (координаты на сфере)
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:
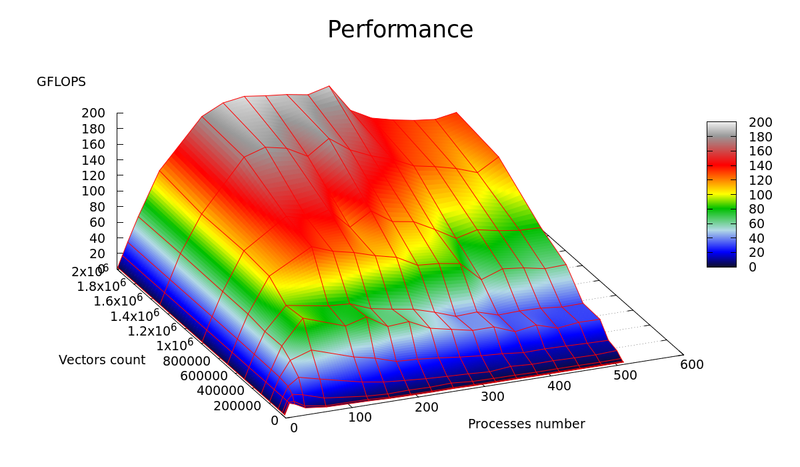
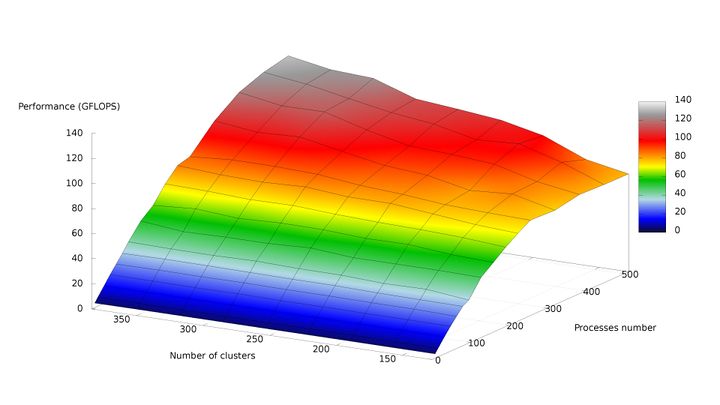
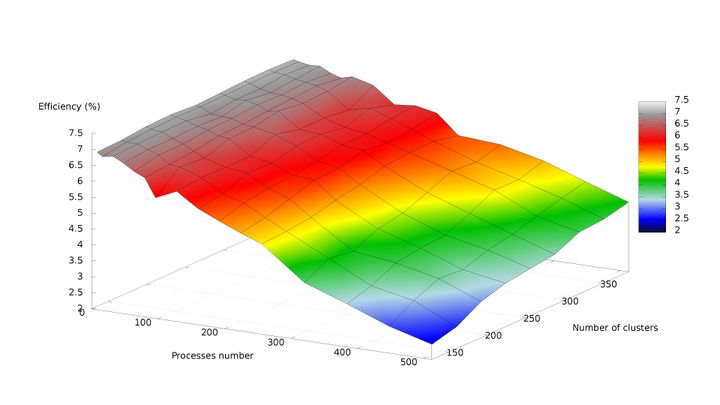
На рисунках 6 и 7, соответственно, представлены графики зависимости производительности и эффективности параллельной реализации k-means от числа кластеров и числа процессов.
По рис. 6 можно отметить практически полное отсутствие роста производительности с увеличением числа процессов от 256 до 512 при минимальном размере задачи. Это связано с быстрым ростом накладных расходов по отношению к крайне низкому объёму вычислений. При росте размерности задачи данный эффект пропадает, и при одновременном пропорциональном увеличении числа кластеров и числа процессов рост производительности становится близким к линейному.
Были получены следующие оценки масштабируемости реализации алгоритма k-means:
2.4.3 Реализация 3
Реализация алгоритма была выполнена на языке программирования C с использованием MPI.
Объем данных составлял 84 ГБ, количество объектов (d-мерных векторов) n равнялось 1,024,767,667, размерность векторов [math]d[/math] равнялась 22, количество кластеров [math]k[/math] равнялось 1000.
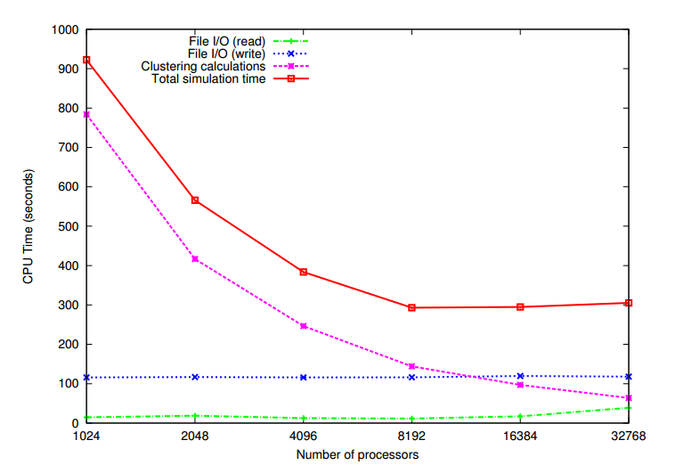
На рис. 8 показана зависимости времени работы алгоритма кластеризации k-means в зависимости от количества используемых процессоров. Можно отметить, что время, затраченное на чтение данных и запись результатов кластеризации, практически не изменяется с увеличением количества задействованных процессоров. Время же работы самого алгоритма кластеризации уменьшается с увеличением количества процессоров.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
Исследуемый набор данных содержит векторы, размерность которых равна 49. Компоненты векторов являются вещественными числами. Количество кластеров равно 11. Пропущенные значения отсутствуют.
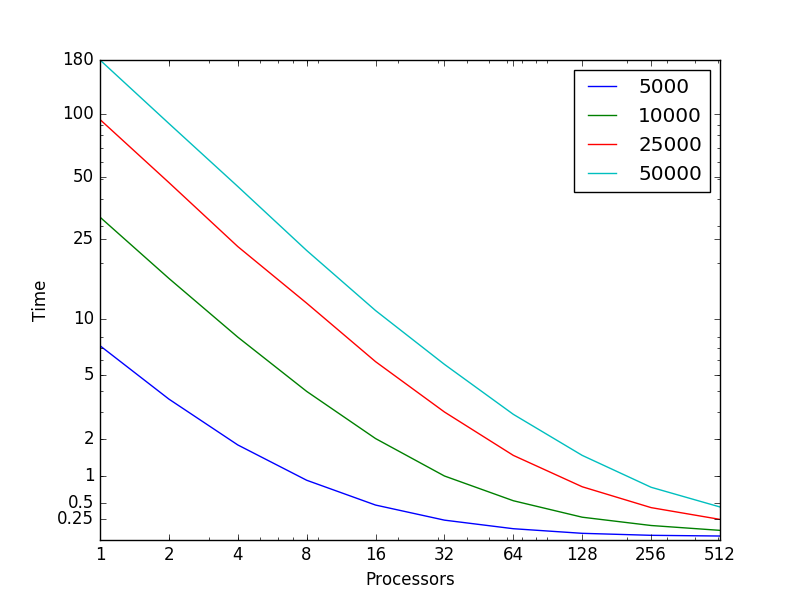
На рис. 9 показана зависимости времени работы алгоритма кластеризации k-means в зависимости от количества используемых процессоров (использовались логарифмические оси). Разными цветами помечены запуски, соответствующие разным количествам объектам, участвующих в кластеризации. Можно видеть близкое к линейному увеличение времени работы программы в зависимости от количества процессоров. Также можно видеть увеличение времени работы алгоритма при увеличении количества объектов.
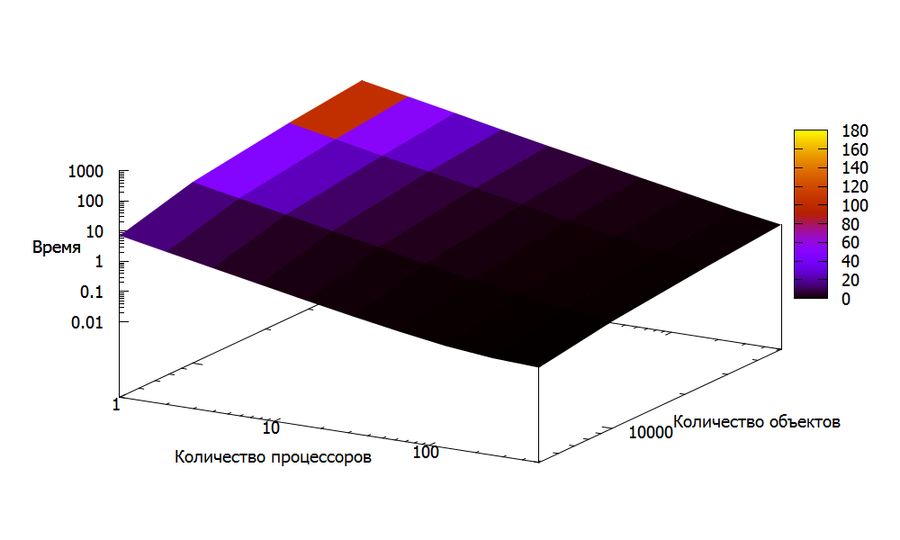
На рис. 10 показана эта же зависимость, только в трехмерном пространстве. По аналогии с рис. 9, были использованы логарифмические оси. Как и в случае двумерного рисунка, можно видеть близкое к линейному увеличение времени работы программы.
2.4.4 Реализация 4
Исследование масштабируемости данной параллельной реализации алгоритма k-средних также проводилось на суперкомпьютере «Ломоносов». Параллельная реализация была написана самостоятельно на языке C, ссылка на реализацию. Так как на каждой итерации число действий на единицу данных не велико и данные должны быть собраны вместе при перерасчете центроидов, было решено для ускорения вычислений воспользоваться только OpenMP без использовании MPI.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
В результате проведённых экспериментов были получены следующие данные:
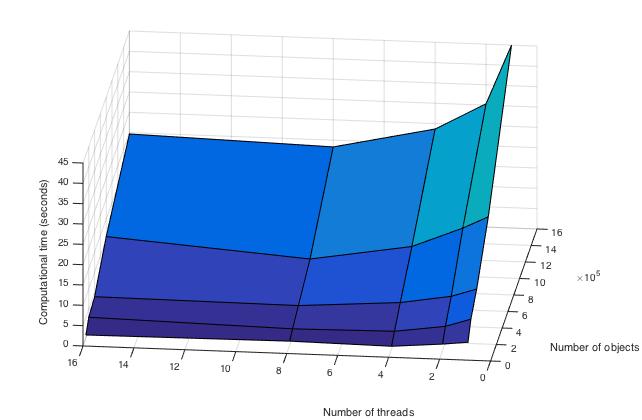
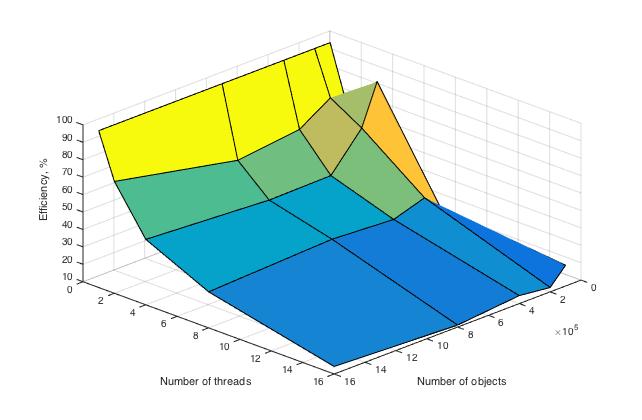
Ниже приведены графики зависимости вычислительного времени алгоритма и его эффективности от изменяемых параметров запуска — размера данных и числа процессоров:
Здесь видно, что время выполнения операций алгоритма плавно убывает по каждому из параметров, причем скорость убывания по параметру числа процессоров выше, чем в зависимости от размерности задачи.
Проведем оценки масштабируемости:
По числу процессов — при увеличении числа процессов эффективность уменьшается на всей области рассматриваемых значений, причем темп убывания замедляется с ростом числа процессов.
По размеру задачи — при увеличении размера задачи эффективность вычислений вначале кратковременно возрастает, но затем начинает относительно равномерно убывать на всей рассматриваемой области.
По размеру задачи — при увеличении размера задачи эффективность вычислений в общем случае постепенно убывает. На малых данных она выходит на пик мощности, являющийся максимумом эффективности в исследуемых условиях, но затем возвращается к процессу убывания.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
В однопоточном режиме на наборах данных, представляющих практический интерес (порядка нескольких десятков тысяч векторов и выше), время работы алгоритма неприемлемо велико. Благодаря свойству массового параллелизма должно наблюдаться значительное ускорение алгоритма на многоядерных архитектурах (Intel Xeon), а также на графических процессорах, даже на мобильных вычислительных системах (ноутбуках), оснащенных видеокартой. Алгоритм k-means также будет демонстрировать значительное ускорение на сверхмощных вычислительных комплексах (суперкомпьютерах, системах облачных вычислений [18] ).