время обучения нейронной сети
Digitrode
цифровая электроника вычислительная техника встраиваемые системы
Что такое скорость обучения нейронной сети
В предыдущей статье мы рассмотрели основы теории обучения нейронных сетей. В данном материале углубимся в эту теорию дальше и поговорим о скорости обучения.
Как вы уже догадались, скорость обучения влияет на быстроту обучения вашей нейронной сети. Но это еще не все.
Во-первых, давайте проясним, что мы подразумеваем под «обучением». В контексте нейронных сетей «учиться» более или менее эквивалентно по значению «обучению», но с другой стороны. Инженер обучает нейронную сеть, предоставляя данные обучения и выполняя процедуру обучения. В то время как это происходит, сеть учится – или, более конкретно, она учится приближать отношение ввода-вывода, содержащееся в данных обучения. Проявлением обучения является изменение веса, а скорость обучения влияет на способ изменения веса.
В предыдущей статье была представлена концепция чаши ошибок, то есть трехмерной поверхности, которая помогает нам визуализировать процесс, посредством которого ошибка узла постепенно уменьшается до нуля, так как его входные веса изменяются во время обучения.
Если у нас есть точка, местоположение которой определяется значениями двух весов и выходной ошибкой узла, каждая модификация весов заставляет точку перескакивать в другое место где-нибудь на этой поверхности ошибки. Эти прыжки имеют тенденцию к нижней части чаши, где ошибка сводится к минимуму; они не приводят непосредственно к минимальной ошибке, потому что каждая обучающая выборка – только маленький кусочек математической головоломки.
Скорость обучения влияет на размер скачков, которые ведут к нижней части чаши. Сейчас мы собираемся перейти к двумерному представлению, потому что так изображения можно будет легче интерпретировать. Вот наша двумерная функция ошибок.
Как вы помните из предыдущей статьи, мы использовали следующее правило обучения для обновления весов:
Здесь α – это скорость обучения, а δ – разница между ожидаемым выходным сигналом и расчетным выходным сигналом (то есть ошибкой). Каждый раз, когда мы применяем это правило обучения, вес переходит в новую точку на кривой ошибки. Если δ велико, эти скачки также могут быть довольно большими, и сеть может не обучаться эффективно, потому что веса не сходятся постепенно к минимальной ошибке. Вместо этого они несколько хаотично перепрыгивают, как показано на следующем изображении.
Поскольку δ умножается на скорость обучения, прежде чем модификация применяется к весу, мы можем уменьшить размер скачков, выбрав α
Понятие скорости обучения в нейронных сетях
В данной статье обсуждается скорость обучения, которая играет важную роль в обучении нейронной сети.
Добро пожаловать в серию статей по основам нейронных сетей. Чтобы узнать о нейронных сетях перцептрон и теории обучения нейронных сетей в целом, ознакомьтесь с содержанием серии выше, в меню над статьей.
В этой статье мы обсудим концепцию скорости обучения и выясним, как она может повлиять на обучение нейронной сети.
Что такое скорость обучения?
Как вы уже догадались, скорость обучения влияет на скорость, с которой обучается ваша нейронная сеть. Но это еще не всё.
Во-первых, давайте проясним, что мы подразумеваем под «обучением». В контексте нейронных сетей «учиться» по значению более или менее эквивалентно «тренироваться», но с другой стороны это разные вещи. Инженер обучает нейронную сеть, предоставляя обучающие данные и выполняя процедуру обучения. В то время как это происходит, сеть учится – или, более конкретно, она учится аппроксимировать связь вход-выход, содержащуюся в обучающих данных. Проявлением обучения является изменение веса, а скорость обучения влияет на способ этого изменения.
Минимизация ошибок в нейронных сетях
В предыдущей статье была представлена концепция чаши ошибки, то есть трехмерной поверхности, которая помогает нам визуализировать процесс, посредством которого ошибка узла постепенно уменьшается до нуля по мере того, как его входные весовые коэффициенты изменяются во время обучения.
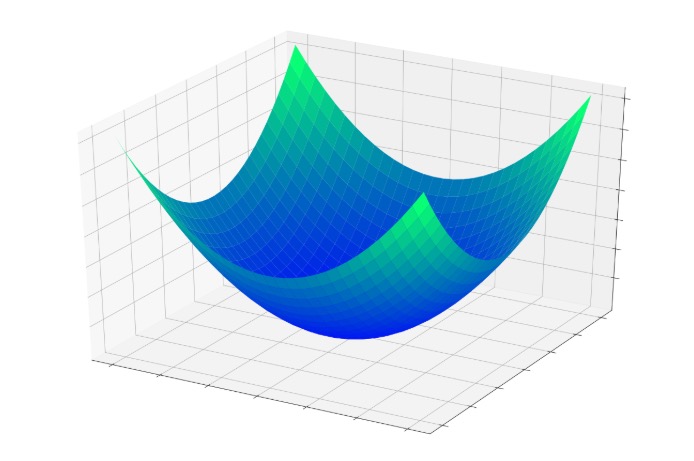
Если у нас есть точка, местоположение которой определяется значениями двух весов и выходной ошибкой узла, каждая модификация весов заставляет точку перескакивать в другое место где-нибудь на этой поверхности ошибки. Эти прыжки стремятся к нижней части чаши, где ошибка сводится к минимуму; они не приводят напрямую к минимальной ошибке, потому что каждая обучающая выборка – это только маленький кусочек математической головоломки.
Влияние скорости обучения
Скорость обучения влияет на размер прыжков, которые ведут к нижней части чаши. Сейчас я собираюсь перейти к двумерному представлению, потому что будет легче создавать и интерпретировать изображения. Вот наша двумерная функция ошибки:
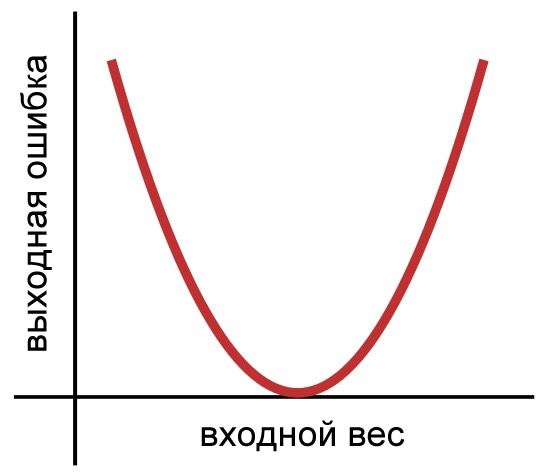
Как вы помните из предыдущей статьи, для обновления весов мы использовали следующее правило обучения:
\[w_ <новый>= w+(\alpha\times\delta\times вход)\]
где \(\alpha\) – это скорость обучения, а \(\delta\) – это разница между ожидаемым выходным сигналом и рассчитанным выходным сигналом (то есть ошибка).
Каждый раз, когда мы применяем это правило обучения, вес переходит в новую точку на кривой ошибки. Если \(\delta\) велика, эти скачки также могут быть довольно большими, и нейросеть может обучаться неэффективно, потому что веса не сходятся постепенно к минимальной ошибке. Вместо этого они хаотично прыгают, как показано ниже.
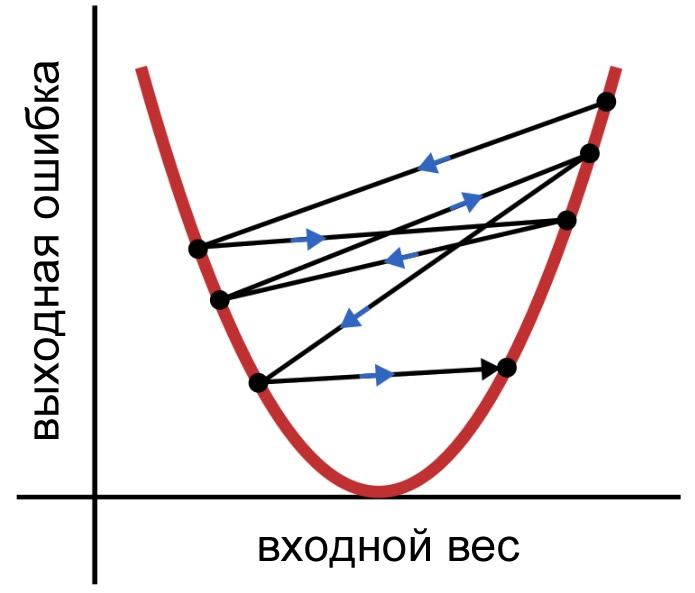
Так как, прежде чем модификация применяется к весу, \(\delta\) умножается на скорость обучения, мы можем уменьшить размер прыжков, выбрав \(\alpha\) 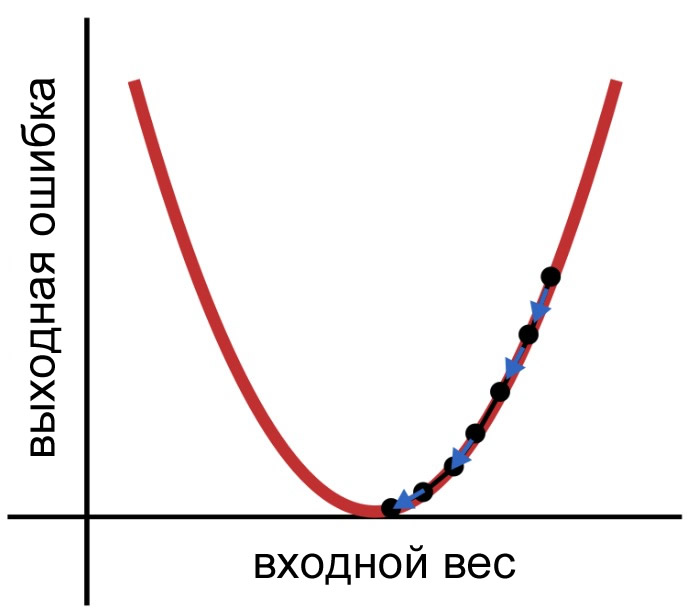
Как выбрать скорость обучения
Не существует универсального правила, которое говорит вам, как выбрать скорость обучения, и нет даже точного и аккуратного способа определить оптимальную скорость обучения для заданного приложения. Обучение – это сложный и изменчивый процесс, и когда дело доходит до скорости обучения, вы должны полагаться на интуицию и эксперименты.
Если ваша нейросеть может быстро обрабатывать обучающие данные, вы можете просто выбрать несколько разных скоростей обучения и сравнить полученные веса (если вы знаете, какими они должны быть) или ввести свежие данные и оценить взаимосвязь между скоростью обучения и точностью классификации.
Более сложный подход, который был бы более практичным для нейросетей, требующих длительного времени обучения, заключается в анализе изменений в ошибках во время обучения сети. Ошибка должна уменьшаться в направлении минимума, а изменения в ошибке должны быть достаточно малыми, чтобы избежать «прыгающего» поведения, показанного выше, но не настолько маленькими, чтобы нейросеть обучалась крайне медленно. Как и многие другие вещи в жизни, скорость обучения зависит от баланса.
О том, как найти оптимальную скорость обучения, можно сказать гораздо больше, и, возможно, мы рассмотрим этот вопрос более подробно в следующей статье. Но не сегодня.
График скорости обучения
Прежде чем мы закончим, я хочу кратко обсудить технику обучения, которая, я считаю, является важным инструментом для тех, кто работает с нейронными сетями. Первое, что нужно признать, это то, что скорость обучения не обязательно должна быть постоянной на протяжении всей процедуры обучения. Скорость обучения используется каждый раз, когда с помощью правила обучения обновляются веса; таким образом, если скорость обучения изменяется во время обучения, то тут же будет изменен и эволюционный путь нейросети к ее окончательной форме.
Одним из способов воспользоваться этим является снижение скорости обучения во время обучения. Это называется «отжигом» (annealing) скорости обучения. Есть разные способы реализовать это, но сейчас важно понять, почему это помогает.
Когда нейросеть начинает обучение, ошибка, вероятно, будет большой. Более высокая скорость обучения помогает нейросети делать большие шаги в направлении минимальной ошибки. Однако когда сеть приближается к нижней части кривой ошибки, эти длинные шаги могут препятствовать сходимости, подобно тому, как человеку, делающему длинные шаги, может быть трудно попасть прямо в середину небольшого круга, нарисованного на полу. Когда скорость обучения уменьшается, длинные шаги становятся меньшими шагами, и, в конце концов, нейросеть приближается к центру круга.
Заключение
Я предупреждал вас в первой статье, что это будет длинная серия. Это уже шестая статья, а конца еще не видно. В любом случае, я надеюсь, что вам понравилось это объяснение скорости обучения. В следующей статье мы обсудим проблему «локальных минимумов».
Оценка оптимальной скорости обучения для глубокой нейронной сети
Дата публикации Nov 13, 2017
Скорость обучения является одним из наиболее важных гиперпараметров для настройки глубоких нейронных сетей.
В этом посте я описываю простой и эффективный способ найти разумную скорость обучения, на которой я училсяfast.ai Курс глубокого обучения, Я принимаю новую версию курса лично вУниверситет Сан-Франциско, Это еще не доступно для широкой публики, но будет в конце года вcourse.fast.ai(которая в настоящее время имеет прошлогоднюю версию).
Как скорость обучения влияет на обучение?
Модели глубокого обучения обычно обучаются оптимизатором стохастического градиентного спуска. Существует множество вариаций стохастического градиентного спуска: Адам, RMSProp, Адаград и т. Д. Все они позволяют установить скорость обучения. Этот параметр сообщает оптимизатору, как далеко нужно переместить веса в направлении, противоположном градиенту для мини-партии.
Если скорость обучения низкая, то обучение будет более надежным, но оптимизация займет много времени, потому что шаги к минимуму функции потерь крошечные.
Если скорость обучения высока, то обучение может не сходиться или даже расходиться. Изменения веса могут быть настолько значительными, что оптимизатор пересекает минимум и усугубляет потерю.
Обучение должно начинаться с относительно большой скорости обучения, потому что вначале случайные веса далеки от оптимальных, и затем скорость обучения может уменьшаться во время тренировки, чтобы обеспечить более детальные обновления веса.
Там должно быть умнее
Лесли Н. Смит описывает мощный метод выбора диапазона скоростей обучения для нейронной сети в разделе 3.3 статьи 2015 года «Циклические учебные курсы для обучения нейронных сетей»
Хитрость заключается в том, чтобы обучать сеть, начиная с низкой скорости обучения, и экспоненциально увеличивать скорость обучения для каждой партии.
Запишите скорость обучения и потери обучения для каждой партии. Затем составьте график потерь и скорости обучения. Как правило, это выглядит так:
Во-первых, при низких скоростях обучения потеря улучшается медленно, затем обучение ускоряется, пока скорость обучения не станет слишком большой и потеря не увеличится: процесс обучения расходится.
Нам нужно выбрать точку на графике с самым быстрым уменьшением потерь. В этом примере функция потерь быстро уменьшается, когда скорость обучения составляет от 0,001 до 0,01.
Это выглядит слишком шумно, давайте сгладим его с помощью простого скользящего среднего.
Это выглядит лучше На этом графике нам нужно найти минимум. Это близко к lr = 0,01.
Реализация
Джереми Ховард и его команда вUSF Data Instituteразработаныfast.aiбиблиотека глубокого обучения, представляющая собой абстракцию высокого уровня поверх PyTorch. Это простой в использовании и в то же время мощный набор инструментов для обучения современным моделям глубокого обучения. Джереми использует библиотеку в последней версии курса Deep Learning (fast.ai).
Библиотека обеспечивает реализацию искателя скорости обучения Вам нужно всего две строчки кода, чтобы отобразить потерю скорости обучения для вашей модели:
В библиотеке нет кода для определения скорости изменения функции потерь, но вычислить тривиально:
Обратите внимание, что однократного выбора скорости обучения перед тренировкой недостаточно. Оптимальная скорость обучения снижается во время тренировки. Вы можете периодически повторять одну и ту же процедуру поиска скорости обучения, чтобы найти скорость обучения на более позднем этапе процесса обучения.
Реализация метода с использованием других библиотек
Я не видел готовых использовать реализации этого метода поиска скорости обучения для других библиотек, таких как Keras, но писать его было бы тривиально. Просто запустите тренировку несколько раз, по одной мини-партии за раз. Увеличьте скорость обучения после каждой мини-партии, умножив ее на небольшую константу. Остановите процедуру, когда потеря становится намного выше, чем ранее наблюдаемое наилучшее значение (например, когда потеря тока> лучшая потеря * 4).
Это еще не все
Бумагачто я упоминал выше, описывает новый способ циклического изменения скорости обучения. Этот метод повышает производительность сверточных нейронных сетей для различных задач классификации изображений.
Пожалуйста, отправьте мне сообщение, если вы знаете другие интересные советы и рекомендации для обучения глубоких нейронных сетей.
Медицинская нейроинформатика
Стратегия и тактика обучения нейронных сетей
Под стратегией обучения нейросетей понимается общий план обучения, включающий разбивку задачи на подзадачи, определение типа и количества нейросетей, обучаемых по каждой из них, предварительные параметры сетей, планирование действий в случае возможных затруднений.
Тактика представляет собой возможное вмешательство оператора в процесс обучения с целью его ускорения, подстройки некоторых параметров, а также оптимальные действия при невозможности дальнейшего обучения сети.
Сформулируем цель обучения, на достижение которой направлены стратегия и тактика. Целью будем считать полное на данном задачнике обучение нейросети (набора нейросетей-экспертов) с минимально возможным числом подстраиваемых связей, максимально возможной характеристикой и максимально возможным уровнем надежности (минимальным уровнем отклонения). Дополнительным условием может быть минимальное (или определенное пользователем) число входных сигналов.
Рассмотрим, как влияют на качество и длительность обучения некоторые параметры. В таблица 5.3 сведены зависимости между обучением (требуемым временем и качеством) сети, ее параметрами, особенностями задачи и используемого компьютера.
| Параметр | Длительность обучения | Качество обучения |
|---|---|---|
| Увеличение тактовой частоты компьютера | 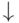 | — |
| Вывод информации в процессе обучения на экран в графическом режиме (по сравнению с текстовым режимом) | 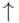 | — |
| Увеличение количества примеров | 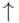 | 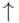 |
| Увеличение количества обучающих параметров | 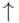 | 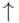 |
| Увеличение количества классов (в классификаторах) | 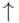 | 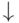 |
| Увеличение размерности вектора ответа (в предикторах) | 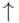 | 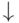 |
| Близкое количество примеров каждого класса (в классификаторах) | 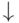 | 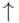 |
| Повышение уровня надежности (в классификаторах) |  |  |
| Повышение уровня отклонения (в предикторах) |  |  |
| Увеличение числа нейронов | 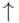 | 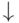 |
| Увеличение параметра плотности | 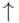 | 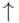 |
| Увеличение времени отклика сети | 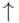 | 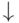 |
| Увеличение характеристики | 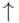 | 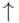 |
В случае предикторов используется понятие уровня отклонения, который определяет максимальное расхождение между требуемым (заранее известным) и вычисляемым сетью ответами, при котором пример считается правильно распознанным. При этом качество обучения тем выше, чем меньший уровень отклонения позволяет сети тестировать все примеры правильно, т.е. увеличивается точность ответа сети. Автоматический режим при этом снижает уровень отклонения после каждого полного обучения. Минимально возможный уровень отклонения равен нулю (абсолютное совпадение ответов) и практически не может быть достигнут.
Изменение весов классов.
Разделение задачи.
После успешного обучения по вышеприведенным схемам желательно переобучить сети с повышением характеристики, особенно в случае недостаточно удовлетворительных результатов контрольного тестирования.
В общем случае, уменьшение количества связей нейросети (путем контрастирования существующей сети или обучения новых сетей с меньшим числом нейронов и плотностью) лучше всего производить в последнюю очередь, после того, как были настроены предыдущие параметры и результаты тестирования по-прежнему высоки. То же касается и минимизации входных параметров, которая, так же как и принципы автоматической стратегии, будут рассмотрены ниже.
Тактика обучения.
В подавляющем большинстве случаев при обучении сети не требуется никакого вмешательства в этот процесс. Однако все же бывают ситуации, когда сеть не может обучаться. Здесь требуются некоторые действия пользователя, которые мы называем «тактикой обучения». Как правило, нейросеть перестает обучаться не сразу, а через некоторое время после начала процесса. При этом нейросетевая программа сигнализирует оператору о невозможности дальнейшего обучения и в простейшем случае останавливает процесс.
Частое применение удара небольшого уровня может быть полезным для создания помехоустойчивых нейросетей.
Невозможность дальнейшего обучения в классификаторах иногда может быть спровоцирована неверной постановкой задачи, точнее, заданной классификационной моделью. Например, при бинарной классификации примеры одного из классов представляют на самом деле два различных подкласса, группирующихся по параметрам «по разные стороны» от другого класса задачи. В этом случае можно использовать нейросеть для коррекции классификационной модели путем кластеризации примеров.
Как уже говорилось, изменение весов классов может считаться тактическим действием, так как может осуществляться прямо в процессе обучения. Поводом для изменения веса класса обычно служит его средняя оценка, значительно (в несколько раз) превосходящая оценки остальных классов.
Стэнфордский курс: лекция 6. Обучение нейросетей, часть 1
В прошлый раз мы обсудили историю возникновения свёрточных архитектур, а также узнали об их устройстве и широких возможностях применения. В течение следующих двух лекций мы поговорим об особенностях обучения нейросетей и разберёмся, как правильно настраивать параметры, выбирать функцию активации, подготавливать данные и добиваться успешных результатов.
Обучение нейросети — непредсказуемый и захватывающий процесс, который, однако, требует тщательной подготовки. В целом его можно разделить на три основных этапа:
В этой лекции мы обсудим некоторые детали первых двух пунктов. Если вы уже знакомы со всеми понятиями и имеете опыт работы с нейросетями, рекомендуем нашу статью с полезными советами по обучению моделей.
Обучение нейросети — непредсказуемый и захватывающий процесс, который, однако, требует тщательной подготовки. В целом его можно разделить на три основных этапа:
Сюда входят: выбор функции активации, предварительная обработка данных, инициализация весов, регуляризация, градиентная проверка.
Отслеживание процесса обучения, оптимизация и обновление гиперпараметров.
В этой лекции мы обсудим некоторые детали первых двух пунктов. Если вы уже знакомы со всеми понятиями и имеете опыт работы с нейросетями, рекомендуем нашу статью с полезными советами по обучению моделей.
Функция активации
Ранее мы выяснили, что в каждый слой нейросети поступают входные данные. Они умножаются на веса полносвязного или свёрточного слоя, а результат передаётся в функцию активации или нелинейность. Мы также говорили о сигмоиде и ReLU, которые часто используются в качестве таких функций. Но список возможных вариантов не ограничивается только ими. Какой же следует выбирать?
Рассмотрим наиболее популярные функции активации и обсудим их преимущества и недостатки.
Сигмоида
Функция сигмоиды преобразовывает поступающие в неё значения в вещественный диапазон [0, 1]. То есть, если входные данные окажутся большими положительными значениями, то после преобразования они будут равны примерно единице, а отрицательные числа станут близки к нулю. Это довольно популярная функция, которую можно интерпретировать как частоту возбуждения нейрона.
Но если внимательнее присмотреться к сигмоиде, можно заметить несколько проблем.
1. Насыщенные нейроны могут «убить» градиент. Возьмём сигмоидный узел вычислительного графа и передадим в него входные данные X. Когда мы делаем обратный проход, восходящий градиент равен dL/d𝜎, а локальный — dL/d𝜎 * d𝜎/dx.
Что же произойдёт, если X будет равен −10? Градиент станет нулевым, поскольку все большие отрицательные значения находятся на прямом участке сигмоидной функции. Таким образом, во все последующие узлы будут передаваться нулевые производные — это и «убивает» градиентный поток.
А если X = 0? В этом случае всё будет в порядке, как и для других близких к нулю значений. А вот при X = 10 градиент снова обнулится. Поэтому сигмоида не работает для слишком высоких положительных или отрицательных данных.
2. Выходные значения сигмоиды не центрированы нулем. Пусть исходные данные полностью положительны — что тогда станет с градиентами во время обратного распространения? Они все будут либо положительными, либо отрицательными (в зависимости от градиента f). Это приведёт к тому, что все веса при обновлении также будут либо увеличены, либо уменьшены, и градиентный поток станет зигзагообразным.
Поэтому следует изначально подготавливать данные таким образом, чтобы их средним значением являлся ноль.
3. Функцию exp() достаточно дорого считать. Это не такая существенная проблема, поскольку скалярные произведения во время свёртки тратят гораздо больше вычислительных мощностей, но в сравнении с остальными функциями активации её тоже можно отметить.
Тангенс
Тангенс очень похож на сигмоиду, но обладает двумя существенными отличиями: он преобразует данные в диапазон [-1, 1] и имеет нулевое центрирование, что исключает вторую проблему сигмоиды. Значения градиента при обратном распространении по-прежнему могут обнуляться, тем не менее, использование тангенса обычно более предпочтительно.
ReLU
ReLU или Rectified Linear Unit стала довольно популярной в последние годы. Она вычисляет функцию f(x) = max(0,x), то есть просто выдаёт значения «ноль» и «не ноль». Это решает проблему обнуления градиента для положительных чисел. Кроме того, ReLU очень просто вычисляется: примерно в шесть раз быстрее сигмоиды и тангенса. Однако, в ней снова отсутствует нулевое центрирование.
Другой очевидный недостаток — градиент по-прежнему «умирает» при отрицательных входных данных. Это может привести к тому, что половина нейронов будет неактивна и не сможет обновляться.
Проблему можно попробовать решить, задав более низкую скорость обучения и подобрав другие весовые коэффициенты. Или использовать модификации ReLU.
Leaky ReLU
Отличие этой функции в том, что она имеет небольшой наклон в левой полуплоскости — значит, при отрицательных входных данных градиент не будет нулевым.
При этом функцию по-прежнему легко вычислить. То есть, она решает практически все перечисленные проблемы. Одной из её разновидностей является PReLU, которая выглядит как f(x) = max(𝛼x, x).
ELU
Эта функция похожа на leaky ReLU и обладает всеми её преимуществами, но включает в себя экспоненту, что делает её вычисление дороже. Её стоит использовать в тех случаях, когда вам важна устойчивость к шумовым данным.
Maxout
Maxout выбирает максимальную сумму из двух наборов весов, умноженных на исходные данные с учётом смещения. Тем самым он обобщает ReLU и leaky ReLU, не обнуляя градиент. Но, как можно догадаться по виду функции, maxout требует удвоения параметров и нейронов.
Подводя итог: используйте ReLU, можете попробовать взять leaky ReLU/Maxout/ELU. На тангенс и сигмоиду лучше не рассчитывать.
Подготовка данных
Существует три наиболее распространённых способа предварительной обработки данных. Будем полагать, что данные X — это матрица размером [NxD].
2. Нормализация. Изменение данных таким образом, чтобы они все были приблизительно одного масштаба. Один из вариантов — разделить каждое измерение на его стандартное отклонение: (X /= np.std(X, axis = 0)). Другой вариант — нормализовать каждое значение так, чтобы min и max были равны -1 и 1 соответственно. Нормализацию следует применять только в том случае, если исходные данные имеют разные форматы или единицы измерения. У изображений значения пикселей не выходят за пределы диапазона от 0 до 255, поэтому для них нет необходимости выполнять нормализацию.
Инициализация весов
Итак, мы построили архитектуру нейронной сети и подготовили данные. Прежде чем начать обучение, необходимо инициализировать параметры (веса).
Как не нужно делать: задавать веса нулевыми. Это приведёт к тому, что абсолютно все нейроны будут вести себя одинаково — совсем не то, что мы хотим получить. Нейросеть должна обучаться разным признакам.
Небольшие случайные величины. Более удачный вариант — присвоить весам маленькие значения. Тогда все нейроны будут уникальными и в процессе обучения постепенно интегрируются в различные части сети. Реализация может выглядеть так: W = 0.01* np.random.randn(D,H). Метод randn(n) формирует массив размера n х n, элементами которого являются случайные величины, распределённые по нормальному закону с математическим ожиданием 0 и среднеквадратичным отклонением 1 (распределение Гаусса). Недостаток этого способа в том, что он неплохо работает для небольших архитектур, но гораздо хуже справляется с громоздкими нейросетями.
Калибровка с помощью 1/sqrt(n). Проблема вышеупомянутого метода состоит в том, что дисперсия случайных величин растёт с числом нейронов. Чтобы избежать этого, можно масштабировать веса, поделив их на корень из количества входов: w = np.random.randn(n) / sqrt(n). Это гарантирует, что все нейроны сети изначально будут иметь примерно одинаковое выходное распределение.
Также можно использовать вариант w = np.random.randn(n) * sqrt(2.0/n), который был предложен в одном из исследований. Он приводит к наиболее удачному распределению нейронов, поэтому на практике рекомендуем использовать именно его.
Пакетная нормализация
Метод, известный также как batch normalization, решает множество проблем при инициализации, заставляя все активации (выводы) принимать единичное гауссово распределение в начале обучения.
Как же это работает? Рассмотрим небольшое число выводов нейронов на каком-либо слое. Пусть в функцию активации поступает вектор размерности d: x = (x(1),…,x(d)). Нормализуем его по каждой из размерностей:
Где E(x) — математическое ожидание, D(x) — дисперсия, которые вычисляются по всей обучающей выборке. Таким образом, вместо инициализации весов можно использовать эту простую дифференцируемую функцию и получить нормальное распределение на каждом слое.
Пакетная нормализация обычно применяется между слоями (полносвязными или свёрточными) и функциями активации.
Это очень полезный алгоритм, который часто применяется в современном машинном обучении. Нейросети, использующие batch normalization, значительно более устойчивы к плохой инициализации.
За нейросетью глаз да глаз
Мы выбрали архитектуру сети, подготовили данные, инициализировали веса и нормализовали их. Пришло время начать обучение! Вернее, попытаться начать. Самый простой способ проверить, что нейросеть готова обучаться — взять совсем немного данных и попробовать переобучить её на них, то есть, добиться очень хорошей точности и малых потерь. Для этого мы убираем регуляризацию, устанавливаем необходимое количество эпох обучения и вычисляем потери (они должны уменьшаться).
Напомним, что эпоха — один «проход» данных через нейросеть, после которого обновляются веса с помощью градиентного спуска. Упрощённо это выглядит следующим образом:
Теперь можно запустить настоящий процесс: взять все данные, добавить регуляризацию и установить начальную скорость обучения. К сожалению, просто выполнить код и оставить нейросеть на пару часов пока не получится. Необходимо убедиться, что потери постепенно уменьшаются после каждой эпохи. Если этого не происходит, скорее всего, скорость обучения слишком маленькая. Стремительный рост потерь наоборот говорит о слишком высоком значении learning rate.
Оптимизация гиперпараметров
Как мы могли убедиться, обучение нейронных сетей включает множество этапов настройки гиперпараметров. Наиболее распространенными являются:
— начальная скорость обучения;
— график затухания скорости обучения (например, постоянная затухания);
При желании можно даже модернизировать архитектуру сети, если вам кажется, что она выбрана не слишком удачно.
Learning rate — одно из самых важных значений. Попробуйте поэкспериментировать с различными вариантами и построить графики потерь. На рисунке ниже слева показаны эффекты, возникающие при изменении скорости обучения, а справа — типичная функция потерь при обучении небольшой нейросети на наборе данных CIFAR-10.
Вторая важная вещь, которую следует отслеживать — точность сети на обучающих и оценочных данных. Если поместить их на один график, то можно оценить наличие переобучения, о чём свидетельствуют расходящиеся кривые.
Для поиска оптимальных гиперпараметров стоит написать отдельную функцию, которая будет самостоятельно подбирать их и выполнять оптимизацию. При этом лучше использовать не равномерный поиск (известный также как «перебор по сетке»), а случайный — он чаще всего даёт гораздо более удачные результаты.
Итоги
Кратко изложим всё, что мы узнали про обучение нейросетей из сегодняшней лекции:
— используйте функцию активации ReLU;
— выполняйте предварительную обработку данных (для изображений: вычитайте среднее значение);
— масштабируйте веса при инициализации;
— применяйте пакетную нормализацию;
— следите за процессом обучения;
— оптимизируйте гиперпараметры с помощью случайного поиска.
На следующей лекции мы расскажем ещё о нескольких важных шагах обучения, узнаем про ансамблевые методы и разберёмся, как выполнять передачу обучения (transfer learning) и точную настройку (fine tuning). Пробовали ли вы самостоятельно обучать нейросети? Были ли у вас свои хитрости, или вы полагались на установки по умолчанию? Делитесь с нами успехами и не забывайте задавать вопросы, если что-то непонятно.
Следующие лекции (список будет дополняться по мере появления материалов):
С оригинальной лекцией можно ознакомиться на YouTube.









