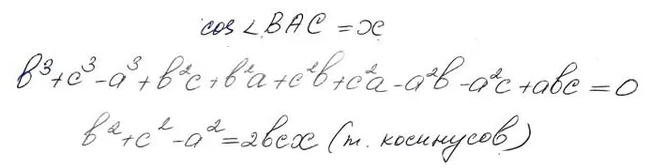Тор что это за фигура

LiveInternetLiveInternet

—Музыка

—Метки

—Рубрики

—Поиск по дневнику

—Друзья

—Постоянные читатели

—Статистика

Эту геометрическую фигуру мы найдем буквально во всем.

В семенах винограда, в воздушных потоках опутывающих нашу планету, форму галактик и всю вселенную.

Давайте выясним, как реальная геометрия реальности влияет на все, что окружает нас и и всё вокруг..

Даже самый маленький объект не говоря об огромных основан на этом универсальном шаблоне.

Квантовая физика, математика и геометрия подтверждают, что Тор в своей блестящей конструкции на самом деле является живой математической формулой, живя и дыша своей жизнью.

ВОЗВРАЩЕНИЕ СЕРДЦА

Человек, конечно же, тоже Тор, а для энергетических полей он является сердцем.

Это прекрасный пример того, что великие мудрецы этого мира говорили на протяжении веков.

Все, что начинается в сердце, в нём и заканчивается.

Энергия Тор делает все, что мы отдаем в любви, возвращается к нам в качестве возвратной эманации в виде подарка.

ТОР В ПРИРОДЕ

Мы видим его в разрезе яблока в форме торнадо, магнитного поля планет или ураганов.

Идя далее, согласно принципу, Тор проявляется в появлении галактик и построении атома.

Энергия Тора проникает в другие тороидальные системы, что можно объяснить одновременной подачей и поглощением.

УНИВЕРСАЛЬНАЯ МОДЕЛЬ ПОДКЛЮЧЕНИЕ ВСЕЛЕННОЙ

Самый красивый факт, в котором существует Тор, состоит в том, что все это совокупная универсальная энергия космоса.

Эта вибрация вызывает наилучшую возможную частоту дыхания Тора, и если наша жизнь наполнена им, мы можем быть уверены, что энергия обратной связи, обусловленная универсальным рисунком, даст нам точно то же самое.

ОТКРЫТИЕ НИКОЛЫ ТЕСЛЫ

Тор, конечно, известен веками.

Гений понимал, что Тор является непрерывным источником энергии, и ключ к развитию планеты скрыт в нем.

Он решил поделиться фантастическими новостями с миром, но силы зла, контролирующие банковское дело на планете, не могли позволить себе потерять контроль.

Изобретения Теслы были разрушены, и сам Тор был забыт.

Метки: тор основы живое реальность вселенная

Процитировано 2 раз
Понравилось: 8 пользователям

Источник

Тор (поверхность)

Обобщенно, тор — топологическое пространство или гладкое многообразие, эквивалентное такой поверхности.

Иногда не требуют, чтобы ось вращения не пересекала образующую окружность. В таком случае, если ось вращения пересекает образующую окружность (или касается её), то тор называют закрытым, иначе открытым.

Понятие тора определяется и в многомерном случае. Тор является примером коммутативной алгебраической группы и примером группы Ли.

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

Говорят, что два и более объектов концентричны или коаксиальны, если они имеют один и тот же центр или ось. Окружности, правильные многоугольники, правильные многогранники и сферы могут быть концентричны друг другу (имея одну и ту же центральную точку), как могут быть концентричными и цилиндры (имея общую коаксиальную ось).

Три вектора (или большее число) называются компланарными, если они, будучи приведёнными к общему началу, лежат в одной плоскости.

В геометрии фигуру называют хиральной (и говорят, что она обладает хиральностью), если она не совпадает со своим зеркальным отображением, точнее, не может быть совмещена с ним только вращениями и параллельными переносами. Хиральная фигура и её зеркальный образ называют энантиоморфами. Слово хиральность происходит от др.-греч. χειρ (хеир) — «рука». Это самый известный хиральный объект. Слово энантиоморф происходит от др.-греч. εναντιος (энантиос) — «противоположный», и μορφη (морфе) — «форма». Нехиральный.

Пра́вильный шестнадцатияче́йник, или просто шестнадцатияче́йник — один из правильных многоячейников в четырёхмерном пространстве. Известен также под другими названиями: гексадекахор (от др.-греч. ἕξ — «шесть», δέκα — «десять» и χώρος — «место, пространство»), четырёхмерный гиперокта́эдр (поскольку является аналогом трёхмерного октаэдра), четырёхмерный кокуб (поскольку двойственен четырёхмерному гиперкубу), четырёхмерный ортоплекс.

Если дано топологическое пространство и группа действий на нём, образы отдельной точки под действием группы действий образуют орбиты действий. Фундаментальная область — это подмножество пространства, которое содержит в точности по одной точке из каждой орбиты. Она даёт геометрическую реализацию абстрактного множества представителей орбит.

Источник

8 необычных геометрических форм, о существовании которых ты вряд ли знал

Какие фигуры ты знаешь? Квадрат, круг, треугольник. Этого вполне достаточно для повседневных задач. Но форм куда больше, чем ты можешь себе представить, и они порой настолько необычные, что кажется, будто их выдумали, просто чтобы потренироваться в фантазии.

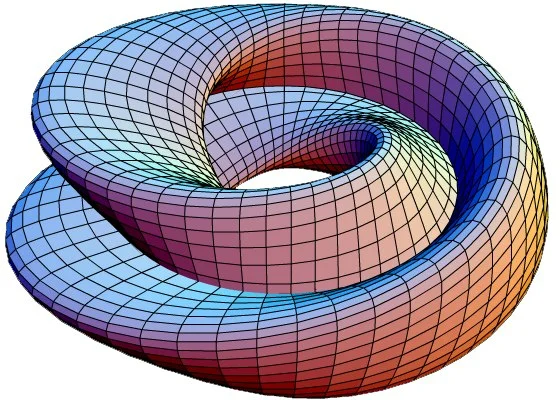
1. Тор

Если говорить научным языком, тор, или, как его ещё называют, тороид, — это поверхность, получаемая вращением образующей окружности вокруг оси, лежащей в плоскости этой окружности и не пересекающей её. Звучит непонятно, и человеку, незнакомому с геометрией, вообще невозможно представить, что это такое.

А на самом деле всё просто, ведь тор ты видишь каждый день — это форма бублика, пончика, спасательного круга, шины колеса и всего похожего на них. Что касается природы, то и в ней встречаются такие фигуры. Например, форму тора имеют вихревые потоки, электромагнитные поля, траектории элементарных частиц.

Так что в следующий раз, когда тебя спросят, какую форму имеет пончик, можешь сказать, что это тор.

2. Треугольник Рёло

Треугольник Рёло — это область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Сам треугольник чем-то напоминает медиатор для гитары и имеет не прямые, а изогнутые грани.

Его ты тоже регулярно встречаешь в обычной жизни. Так, например, треугольник Рёло используют в сфере искусства для уже упомянутых струнных инструментов, а также при рисовании различных диаграмм, где несколько элементов по кругу, сочетаясь между собой, приводят к центральному ядру.

Кроме того, треугольник Рёло — это одна из первых изобретённых человеком форм, так как древние люди, изготавливая свои примитивные орудия труда из камня, нередко обтачивали их именно в такой форме, что позволяло использовать их с любой стороны.

3. Гиперболоид

Гиперболоид — это трёхмерная форма, которая напоминает песочные часы. Существуют однополостные и двухполостные гиперболоиды. Вторые ты можешь увидеть в тех знаменитых тарелках спутниковой связи, а также в телескопах, если интересуешься астрономией. Не путай гиперболоид с гиперболой — это разные вещи.

4. Аполлонийская прокладка, или аполлоническая сетка

Это очень сложная фигура, состоящая из одного большого круга с кругами меньшего размера, которые заполняют пространство внутри него.

Эта фигура редко где используется, и её можно было встретить в старых калейдоскопах, а также в искусстве. В художественных школах иногда ученики рисуют аполлонийские прокладки для отработки навыка рисования ровных кругов от руки.

5. Балбис

Думаешь, что буква Н — это просто буква? На самом деле это геометрическая форма, которую по-простому можно описать как одну первичную линию, которая завершается вторичной линией на одном конце и ещё одной — на другом. Завершающие линии располагаются под прямым углом к первичной, а его параллельные стороны могут быть бесконечно длинными.

6. Лента Мёбиуса

Про эту фигуру ты мог слышать в каких-нибудь фантастических фильмах, да и то редко. Это простейшая неориентируемая поверхность, являющаяся односторонней и непрерывной в трёхмерном пространстве. Лучше увидеть ленту Мёбиуса своими глазами, чтобы понять, что это такое. Если ты хочешь пошутить над человеком, то просто попроси его развернуть ленту Мёбиуса так, чтобы она не изгибалась. Заранее скажем, что сделать это невозможно.

7. «Рыбий пузырь»

Эта фигура больше известна как Vesica piscis, и она образована пересечением двух кругов с одинаковым радиусом, наложенных так, что центр одного лежит на окружности другого.

Где ты мог видеть такую фигуру? К примеру, в эмблеме Audi или Олимпийских игр. Также «рыбий пузырь» можно встретить в средневековой архитектуре в орнаментах и мозаиках.

8. Лемниската

Не зря лемниската идет у нас под восьмым номером, ведь своим видом она напоминает именно эту цифру, а также символ бесконечности. Эта плоская алгебраическая кривая может иметь несколько фиксированных фокусов, и от количества точек будет зависеть её конечная форма.

Источник

Не правда ли завораживает? Какими свойствами обладает это фигура, можно ли ее построить в нашем трехмерном мире, как пройти из одной точки в другую?

Возникает резонный вопрос, а какие свойства остаются неизменными при гомеоморфизме? Математики называют такие свойства качественными или топологическими и если мы хотим говорить о них, то должны как-то охарактеризовать эти свойства, хотя бы интуитивно-наглядно. Очередной эксперимент:

1) Зададимся вопросом: как наикратчайшим образом добраться из одной точки сферы в другую, противоположную ей (например. с северного на южный полюс)? Правильно, пойти как нормальный человек по поверхности. А для шара? Теоретически мы могли бы «срезать» добрую часть путь проникнув через его центр и прошив его насквозь. Есть отличие!

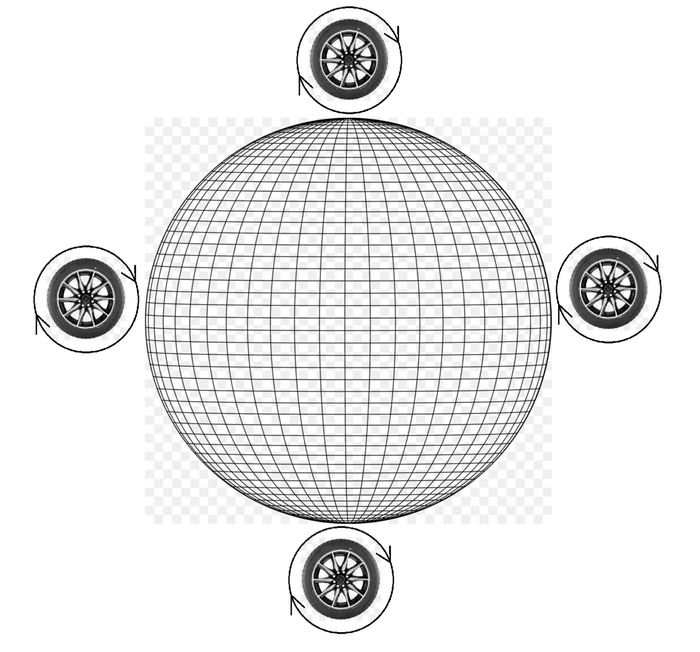
2) Представьте, что вы решили прокатить по поверхности сферы колесо и вернуться в ту же точку. Изменится ли направление его вращения после Вашего с ним кругосветного приключения? Очевидно и для сферы и для шара, что нет.

Именно поэтому у кругосветных путешественников-автомобилистов колеса по приезду в родной город не крутятся в другую сторону

3) Из определения следует, что под поверхностью сферы пустота. В шаре такого нет, он заполнен полностью.

Именно в третьем различии вся «соль». Что же из него следует?

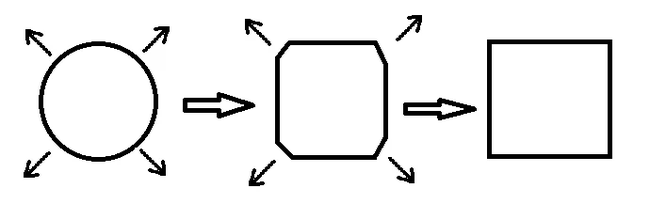
Представьте, что Вы взяли комок мокрого снега и хотите придать ему идеальную форму.

А теперь попробуйте стянуть футбольный мяч хотя бы к одной его точке. Попробуем стянуть северный (N) и южный полюса (S). Суть в том, что в предельном приближении мяч порвется в точках W и E, а разрыв, как мы помним из определения, недопустим при гомеоморфизме.

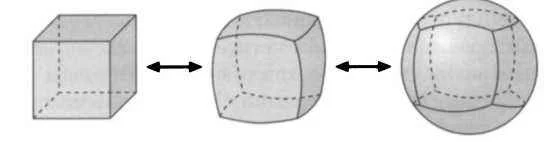
Со сферой всё намного интереснее. Топологи различают сферу без ручки (тогда это просто сфера) и сферу с n-ручками, где n=1,2. Например, сфера с ручкой получается с помощью гомеоморфных преобразований из тора (бублика).

Что же общего у кружки и тора? Ответ: количество дырок, и это ключевое топологическое свойство фигур. Фигуры с разным количеством дырок не могу быть гомеоморфны другу другу, не могут быть получены друг из друга посредством сжатия/растягивания. И это главный вывод нашего вводного экскурса.

Спасибо за прочтение! Материал написан лично мною и взят с канала «Математика не для всех», который да-да-да базируется на платформе Дзен. Сейчас уже вышли три материала по теории множеств ( вот 1, 2 и 3), необходимые для введения в топологию.

Оказывается, там не только чернуха и трэш, но и вполне себе интеллектуальный контент бывает. Буду рад комментариям и подпискам. На данный момент на канал подписано около 300 человек.

Пессимист говорит, что стакан наполовину пуст. Оптимист, что наполовину полон. Тополог говорит, что стакан целиком из стекла, всё остальное снаружи.

Все 20 минут можно не смотреть, в первые две станет все понятно. 🙂

Проблема простых-близнецов – Алексей Савватеев | Научпоп

В чём заключается одна из самых древних проблем «школьной» математики? Почему она называется «простые-близнецы» и как формулируется? Что утверждает теорема о распределении простых чисел в натуральном ряду? Как продвинулась в этой области современная математика и на какие вопросы ещё предстоит найти ответы математикам будущего?

Рассказывает Алексей Савватеев, математик и матэкономист, доктор физико-математических наук, научный руководитель Кавказского Математического Центра АГУ, ректор Университета Дмитрия Пожарского, профессор МФТИ, научный руководитель ЦДПО РЭШ, ведущий научный сотрудник ЦЭМИ РАН, популяризатор математики среди детей и взрослых.

Молдавские учёные решили проблему, над которой 140 лет бились математики всего мира

Два математика из Молдовы первыми в мире решили алгебраическую проблему, над которой 140 лет размышляли великие ученые мира. Об этом на этой неделе сообщил Технический университет Молдовы (UTM).

«Доктор физико-математических наук Михаил Попа и доктор математических наук Виктор Прикоп первыми в мире нашли решение знаменитой проблемы центра и фокуса, поставленной выдающимся французским математиком Анри Пуанкаре, над которой великие математики мира размышляли более века», — говорится на сайте университета.

Этой проблеме посвятили тысячи работ математики из Франции, России, Беларуссии, Китая, Великобритании, Канады, США и других стран мира. Только в Молдове число работ, посвященных проблеме Пуанкаре, приближается к сотне, отметили в UTM.

Профессор университета Михаил Попа, основатель научной школы алгебры Ли и дифференциальных систем, предложил собственное решение проблемы центра и фокуса, которое привело его к результату, ставшему открытием.

Во время исследований к профессору присоединился его ученик Виктор Прикоп. Вместе они усовершенствовали первоначальную гипотезу в монографии «Проблема центра и фокуса. Алгебраические решения и гипотезы».

Работа была переведена на английский язык и представлена для издания в несколько зарубежных издательств. В итоге лучшие условия предложил издательский дом «Taylor & Francis Group», расположенный в Великобритании и специализирующийся на публикациях научной литературы и журналов.

Где-то всплакнул Гриша Перельман.

Панорама, да не та. И с такими лицами не шутят.

Что такое наука и какие задачи она должна решать? Существует ли музыкальная наука и какими могут быть результаты применения научного метода в этой сфере? Что такое микрохроматика и как она может изменить музыку будущего, расширить возможности её создания и восприятия?

Шикарный канал. Жаль тогда ещё подписок не придумали.

Отец поступившей в МГУ девятилетней девочки заявил об угрозах от преподавателей

Преподаватели поступившей на факультет психологии Московского государственного университета (МГУ) имени М. В. Ломоносова девятилетней Алисы Тепляковой отказались искать индивидуальный подход к девочке и якобы угрожали ей отчислением за непосещаемость. Об этом в беседе с «Лентой.ру» рассказал ее отец Евгений.

«Нам необходимо взаимодействие в индивидуальном ключе с педагогами. К сожалению, очень многие преподаватели на текущий момент высказали такую позицию, что никакого вам не будет индивидуального подхода, ничего не будет. Вот есть лекции, а дальше нету времени, денег и вообще нафиг вы нам тут нужны»

По его словам, «существенное количество сотрудников» озвучили такую позицию, однако он не стал называть конкретные фамилии педагогов. При этом Тепляков подчеркнул, что официальная позиция факультета заключается в том, что ситуация с его дочерью решаема и никто ее отчислять не будет.

«Она звучит так: мы ничего вам не будем давать, вы не можете уйти вперед, мы вам не позволим, мы вам не дадим контактов ничьих, мы не будем отвечать на ваши вопросы. Вы будете сидеть вот тут, и мы будем вас оценивать. У вас будет контроль посещаемости, у вас будут проблемы, мы вас отчислим за непосещаемость»

(с) Евгений Тепляков

(о неофициальной позиции МГУ по поводу его 9-летней дочери)

.По словам Теплякова, их семья многократно говорила, что «формальные моменты из образовательной программы Алисы нужно убирать», поскольку ей девять лет и простроить занятия со 100-процентной пос

Чувак не понимает в чем принцип высшего образования. Это не зубрежка знаний, а рефлексия, то есть взаимосвязь эмпирического научного метода с умозаключительным, связывание эксперимента с опытом. А какой у ребенка опыт?

Бедный ребёнок. у девочки явно патологическая активность мозга, которая неизвестно чем и когда кончится. Дай Бог, чтобы она не свихнулась и не умерла от этого. Думаю, что пубертат может многое расставить на свои места и она станет нормальным человеком. Просто непонятно- зачем сейчас лишать ребёнка детства и гнать эту учёбу? Для чего? Что она будет делать потом, если закончит МГУ досрочно? И зачем всё это?

Решил, что буду бесплатно проверять у учеников ежедневные задания

Я преподаватель по математике и с 1 октября 2021 я открываю подготовку к профильной математике ЕГЭ 2022 для всех желающих бесплатно. Подготовка будет идти до самого экзамена. Подробнее можете прочитать о том, как все будет происходить, в моем предыдущем посте на Пикабу.

Решил, что занятия будут полезнее, если к ежедневным заданиям добавить еще и проверку мной работ учеников.

Я буду выборочно проверять работы учеников и писать комментарии ученикам лично, отдавая приоритет тем работам, которые присланы раньше других. А самые полезные для всех моменты из работ буду комментировать для всех. Но предостерегаю, что все это бесполезно без вашей собственной работы и выработки правильных привычек, которые кратно ускоряют обучение. Поэтому и пишу этот пост-дополнение.

Подготовка будет проходить здесь. Изучайте.

О правильных образовательных привычках для учеников я пишу здесь.

Бесплатно помогаю готовиться к профильному ЕГЭ по математике

Недавно я написал о том, как финансовые проблемы у некоторых моих учеников летом помогли мне придумать, как помочь тем, кто хочет сдать ЕГЭ профиль по математике, но не может или не хочет за это платить деньги.

Подготовка будет происходить здесь. Каждый день я буду публиковать задания на день с пошаговыми разборами и отвечать на вопросы по ним. Обязательно подпишитесь на канал, так как пропускать задания не очень хорошо и лучше держать темп ровным, уведомления помогут в этом. Там есть описание, как все будет происходить, а также есть ссылка на пример задания, примерно из середины курса. Он только для примера. На нем можно пощелкать и понять, как смотреть подсказки.

Делать ежедневные задания, их решения и отвечать на вопросы мы будем с вместе с еще одним преподавателем-математиком Дмитрием. Одному было бы тяжело.

Подписанных уже 100 человек, значит точно начинаем. Присоединяйтесь. Начало 1 октября 2021.

Для тех, кто хочет почитать мои мысли, о том, как нужно организовывать обучение, можете посмотреть мою телегу.

Реставрирую шкаф

Работа не быстрая, поэтому фото до. Нашел в нем тайник, в тайнике фото.
Интересует, что за формула на доске?
Пока ответа не нашлось.
Шкаф в СПБ. Ещё была найдена карта Казани печать старая начало 20 века.

Как сделать репетитора бесплатным

Я преподаватель математики. Уже давно готовлю ребят к профильному ЕГЭ по математике. У меня уже сложилась своя методика подготовки, которая из года в год показывает неплохие результаты.

Время от времени у кого-нибудь из учеников случаются финансовые сложности, то ковид, то еще что-то. Таким ученикам, я всегда предлагаю позаниматься бесплатно. Вот и в начале этого лета родители Никиты сообщили мне о трудностях и сказали, что далее обучаться он не сможет. Я предложил продолжить занятия бесплатно до конца лета, а в начале осени либо продолжить платно либо завершить обучение. За лето Никита сильно продвинулся. Осенью Никита выбрал продолжение занятий.

Из, того что я увидел за лето, я сделал интересный вывод. При достаточном уровне прилежности ученика вполне можно построить такую методику, которая будет давать ученику то же самое, что и очные занятия. К сожалению, думаю, что, если ученику особо математика не сдалась, то эффекта от такой подготовки не будет.

Как я работал с Никитой

Каждый день я высылал задание на день, рассчитанное примерно на 0.5-1.5 часа самостоятельной работы.

Разрешение возникающих вопросов

Если все же не получалось решить, то Никита писал мне в WhatsApp, и я присылал ему 1-2 шага решения. Если опять не получалось, то я присылал ему все решение. Обычно это снимало все вопросы.

Если все же остались какие-то вопросы, то он мог задать мне два вопроса в день, и я развернуто ему на них отвечал. Этого было достаточно.

Как решен вопрос с теорией

По каждой теме мной составлена последовательность задач от элементарных (которые может решить каждый) до задач уровня ЕГЭ. Эту последовательность я отлаживал последние пять лет. Удалось сделать так, что основные теоретические моменты включены в решения задач. Поэтому, прорешав последовательность и получив ответы на возникающие вопросы, ученики отлично усваивают теорию.

Приращение сложности от одной задачи к другой минимальное. Поэтому большинство учеников, решив предыдущую задачу, решат и следующую. Так, на дистанции в 10-20 задач незаметно произойдет уже заметное приращение сложности, которое без такой цепочки задач преодолеть было бы практически невозможно.

Раз в неделю Никита решал пробник и записывал свои результаты в табличку, где всем был виден прогресс.

Не так давно стал вести телеграм-канал о том, как организовать обучение, как сделать обучение эффективным, а также ответы на частые вопросы родителей и учеников: https://t.me/dobraya_problema

В результате чего происходит обучение ученика

Я учитель математики. И по роду деятельности постоянно разговариваю с учениками и их родителями на предмет того, что полезно для обучения, а что нет. И часто вынужден говорить «это хорошо, а это плохо». Мне такая ситуация очень не нравится, потому что обосновывать приходится каким-то птичьими обоснованиями типа «так всегда было», «школа такая-то или такая-то» или «британские ученые доказали».

Поэтому решил сформулировать свое представление о базисе, на основании которого можно будет потом делать хоть сколько-нибудь обоснованные выводы. Не судите сторого. Это моя попытка по-простому с помощью аналогий рассказать, как я это представляю ))

Нейроны могут либо возбуждаться в какой-то ситуации, либо не возбуждаться. Возбуждаются они только если поступил определенный сигнал из органов чувств.

Например, если увидеть треугольник, то возбудится нейрон, который отвечает за фигуру треугольник. Он узнает только ее. Причем этот треугольник может быть нарисован на листе бумаги, а может быть, это форма крыши увиденного дома. В обоих случаях нейрон треугольника будет зажжен. В случае, если треугольник был на бумаге, то зажжется еще нейрон, который всегда зажигается при виде бумаги, и еще тысячи других мелких нейронов. Если треугольник был распознан как фигура крыши дома, то зажгутся нейроны дома, крыши, может быть, у кого-то нейроны дождя и т.д.

Некоторые нейроны могут зажигаться не в результате получения сигнала органами чувств, а в случае, если зажглась какая-то комбинация нейронов.

Например, если человек увидел приближающееся к нему животное, то зажгутся нейроны животного, нейроны приближающегося объекта, нейрон размера объекта, нейрон вида объекта. Для простоты допустим, что есть нейрон, который зажигается, когда зажигается комбинация: объект приближается, хищник, большой. Предположим, этот нейрон зажегся. Назовем этот нейрон «нейрон большой зверь идет в мою сторону». Пусть есть нейрон, который зажигается всегда, когда зажигается нейрон «нейрон большой зверь идет в мою сторону». Пусть это будет нейрон «бежать» и т.д.

Решение задач по математике тоже происходит в результате последовательности зажиганий нейронов.

Например, пусть ученик увидел условие задачи, в которой дан прямоугольный треугольник и известны два катета, а найти нужно гипотенузу. В голове образованного ученика зажжется нейрон прямоугольный треугольник. Всегда, когда зажигается нейрон «прямоугольный треугольник» у обученного геометрии человека зажигается нейрон «теорема Пифагора». Если есть два катета и горит нейрон «теорема Пифагора», то зажигается нейрон «я знаю, как найти гипотенузу, зная два катета» и т.д.

Что такое образованность

Образованность в конкретной области — это наличие наработанных цепочек зажигающихся нейронов, которые регулярно приводят к правильным решениям.

Как сформировать такие связи

Связь формируется, если в ответ на ситуацию человек произвел действие и в последствии оказалось, что это действие верное. Т.е. это обычная приспосабливаемость. Причем если в ответ на ситуацию человек произвел действие, а потом оказалось, что оно неверное, то обучение тоже происходит, только такая цепочка нейронов в будущем не будет зажигаться.

В результате чего происходит обучение

Нужно пробовать решать задачи. Нужно решать задачи, которые учитывают уже имеющиеся нейронные связки.

Бесполезно решать легкие задачи: связи уже есть и вы просто их укрепляете, и это укрепление будет даже немного мешать формировать новые связи.

Бесполезно решать слишком сложные задачи, так как не хватает очень больших участков цепи нейронов. И есть риск, что она будет сформирована неправильно, если вы даже где-то прочтете решение.

Нужно решать задачи, которые требуют приращения «одного» звена к цепи нейронов.

Читать теорию, а потом решать задачи менее эффективно, чем просто решать задачи, если эти задачи выстроены в цепочку, где каждая следующая задача требует наличия всего одного звена в нейронной цепочке. Но очень часто люди сначала слушают теорию, а потом пробуют решать задачи. Это происходит потому, что состояние нейронных цепочек у всех разное и подобрать такую последовательность задач индивидуально сложно и проще сначала рассказать теорию, а потом всем решать одни и те же задачи.

Буду рад камментам с предложениями по улучшению/сокращения/исправлению этого объяснения для родителей и учеников!

В своем телеграм-канале отвечаю на частые вопросы родителей и учеников. Заходите.

Земля стационарна, сынок

— Земля крутится, говоришь?

— Земля стационарна, сынок. Она не крутится.

— Но нас по географии учат, что Земля обращается вокруг Солнца.

Классификация ВУЗов и специалистов по С.П. Капице и соавторам

Данная статья относится к Категории: Теория элит

«При рассмотрении проблемы сохранения системы высшего образования существенным, с нашей точки зрения, является выделение трёх категорий ВУЗов, основное различие между которыми состоит не в специальности, по которой производится подготовка студентов, а в масштабах влияния на общество, как текущее, так и перспективное.

Данным категориям ВУЗов отвечает соответствующая классификация людей, занятых в общественном производстве и управлении.

2. «Хранители» существующих жизненно важных технологий. В современном обществе эта группа оказывается довольно тесно связана с первой, поскольку время жизни большинства технологий существенно меньше срока профессиональной деятельности. Тем не менее, провести разграничительную черту всё же можно. Отсутствие или недостаточная подготовка специалистов этой группы приводят к техническим катастрофам различных масштабов из-за снижения уровня производства и обслуживания техники.

Соответственно, можно выделить и три группы учебных заведений.

Капица С.П., Курдюмов С.П., Малинецкий Г.Г., Синергетика и прогнозы будущего, М., «Наука», 1997 г., с.188-189.

Изображения в статье

Сергей Петрович Капица — авиационный инженер (по образованию) и телеведущий программы о науке и учёных «Очевидное – невероятное» / CC BY-SA 4.0

Ох уж этот неформальный математический стиль

Что, если наш 4D мир станет пятимерным?

Краткая текстовая версия видео:

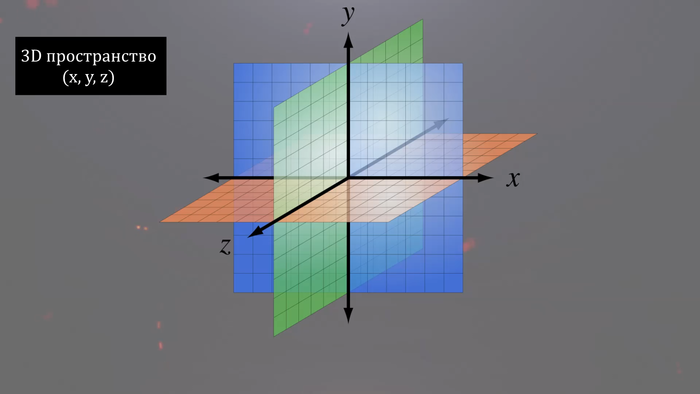
Мир, в котором мы живем, является четырехмерным. По крайней мере в макро масштабе. В нашем мире 3 пространственных измерения и одно временное. Трехмерность пространства значит, например, то, что мы можем в нем провести три взаимно перпендикулярных координатных осей расположенных под углом 90 градусов. В таком пространстве можно двигаться «влево-вправо», «вперед-назад» и «вверх-вниз».

В трехмерном пространстве мы можем завязать узел. В двумерном пространстве завязать узел невозможно. А еще в трехмерном пространстве стул может стоять только на трех ножках или больше, стул на двух ножках потеряет равновесие и упадет (Речь идет о ножках типа такого, как на фото).

А что будет, если мы добавим еще одно пространственное измерение? То есть представим себе пятимерный мир, 4 пространственных измерения и 1 временное?

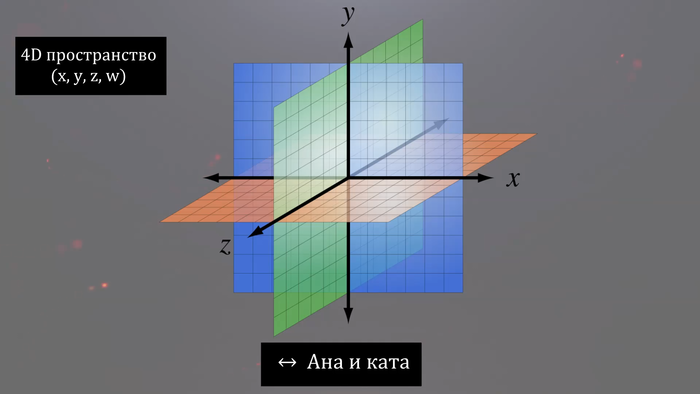
В таком мире можно провести еще одну ось перпендикулярную к остальным трем осям под углом 90 градусов. В трехмерном пространстве сделать это невозможно и как-то точно визуализировать я это не могу, так что включайте фантазию.

В пятимерном мире так же добавятся новые направления движения, которые называют «ана-ката», получается: «влево-вправо», «вперед-назад», «вверх-вниз» и «ана»-«ката». Представить себе направление движения ана и ката мы не можем, так же как существо в двумерном мире не может представить себе направления вверх и вниз.

В таком мире можно завязать двумерную сферу на узел, в нашем мире сделать это невозможно, показать, соответственно, тоже нельзя. Ну и стул с тремя ножками не сможет стоять в мире с 4 пространственными измерениями, чтобы он был устойчив потребуется 4 или больше ножек.

Ну хорошо, я понимаю, вы вряд ли Вы читаете это, чтобы узнать о узлах и ножках стула, Вас интересует, что будет с нашим миром, если внезапно в него добавить еще одно измерение, вот так по щелчку пальца «тыц» и добавили еще одно пространственное измерение и вот ты уже в 5 измерении, что с тобой будет?

Если коротко то… умрешь конечно же. А еще Земля станет приплюснутой. Сейчас расскажу как именно умрешь и почему земля станет приплюснутой.

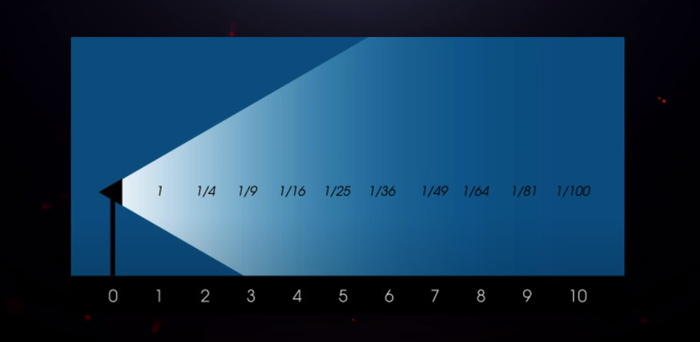
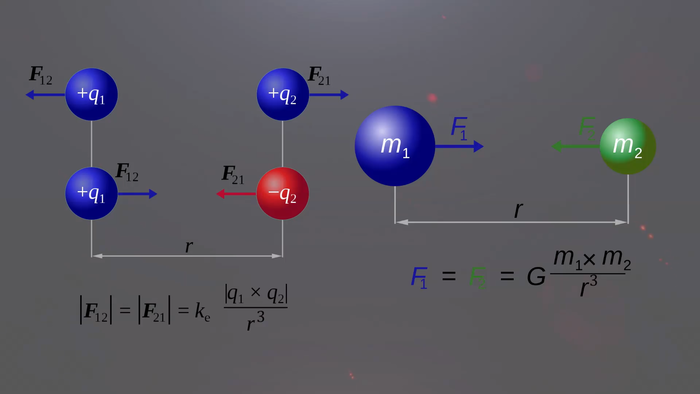
Есть такой закон – закон обратных квадратов, и он тесно связан с размерностью пространства. Возьмем для примера светящий фонарь, интенсивность света в таком случае убывает согласно закону обратных квадратов.

Объект, перемещенный на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении. На расстоянии в 3 раза большее от источника – в 9 раз меньше мощности, на расстоянии в 4 раза большее от источника – 16 раз и так далее.

В законе всемирного тяготения сила гравитационного притяжения убывает тоже с квадратом расстояния. В два раза увеличиваем расстояние, сила притяжения уменьшается в 4 раза и так далее. Тоже самое с законом Кулона – сила притяжения или отталкивания заряженных частиц убывает с квадратом расстояния. В 5D мире закон обратных квадратов превращается в закон обратных кубов. Теперь интенсивность света будет падать не с квадратом расстояния, а с кубом расстояния. r^2 в законе Кулона и Законе всемирного тяготения превращается в r^3.

Это все полностью изменит химические элементы из которых мы состоим, некоторые атомы станут нестабильными, радиоактивными, другие наоборот, станут стабильными.

Например, в 5D мире магний был бы благородным газом, а не металлом, то есть некоторые элементы станут менее реактивными, другие более реактивными. Ионизация атомов будет осуществляться при значительно меньших энергиях, да и вообще агрегатное состояние различных элементов будет меняться не так, как в нашем мире, некоторые хим. элементы станут газообразны при комнатной температуре, некоторые затвердеют и такие вот вещи. Думаю, практически бессмысленно вспоминать биологические процессы, благодаря которым мы можем жить, ведь это все поменяется кардинально, мы мгновенно потеряем сознание и умрем, синтез белков, транспортировка различных аминокислот, нейромедиаторов, нервные импульсы, это все либо прекратится, либо изменится до неузнаваемости. Ну и конечно же спектры атомов изменятся, а это значит, что все резко поменяет цвет, что-то станет прозрачным, что-то непрозрачным, да и вообще привычные для нас источники света выглядели бы более тускло из-за r^3, с запахами та же история, правда уже некому будет смотреть и нюхать все это, ведь все живые существа погибнут.

Короче будет происходить полная жесть, что-то будет плавится, что-то превратится в газ, что-то затвердеет, некоторые вещества станут радиоактивными, привычные нам вещи потеряют свои свойства и перестанут работать так, как в нашем мире. Я напомню, что это все в мире, в котором 4 пространственных измерения и одно временное и в котором можно двигаться в направлении ана и ката. Но кроме дополнительного направления появятся также дополнительные степени свободы во вращении. В нашем мире ориентацию тела можно задать тремя углами, в быту это называется «наклон, подъём и поворот», в 5D мире надо представить себе еще 3 дополнительных степени свободы вращения перпендикулярные к 3 вышеупомянутым. Но по идее, на вращение Земли это не должно повлиять, момент импульса сохранится, ведь нужно, чтобы какая-то сила передала момент импульса Земле, чтобы она могла вращаться в какой-то непривычный для нас способ. Конечно Земля изменит свой привычный облик, из-за того, что свойства химических элементов изменятся, но из-за гравитации все должно также удерживаться вокруг центра масс, правда земля довольно быстро вращается, а так как гравитация в 5D мире у нас ослабевает с кубом расстояния, то земля сплюснется и формой будет напоминать что-то типа такого, как на картинке.

Но вообще, появится дополнительное направление, в котором могут двигаться частицы из которых состоит земля, планета начнет превращаться в гиперсферу, представить себе этот процесс, эти метаморфозы которые будут происходить, очень сложно.

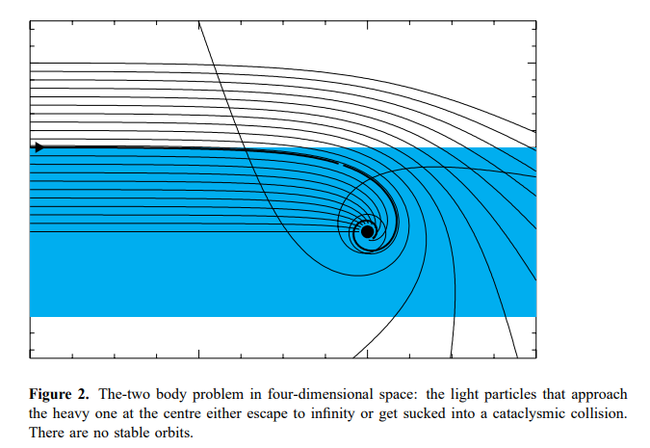
Будут ли происходить термоядерные реакции на солнце, тут под вопросом, но изменения явно произойдут. Но вот что забавно – в пятимерном мире нет стабильных орбит. Вот, посмотрите на график, это моделирование классической задачи двух тел, оказывается, что устойчивых орбит в 5D мире нет, тела либо падают друг на друга, либо улетают в бесконечность, поэтому солнечная система, как и все другие системы, разрушится, некоторые тела упадут на другие тела, а некоторые улетят бороздить просторы галактики.

Казалось бы, следуя логике как с законом обратных квадратов, все квадраты в других уравнениях тоже надо заменить на кубы и получается, что формула эквивалентности массы и энергии в пятимерном пространстве будет работать как Е=мс в кубе, но нет, эта формула, как и множество других, не изменятся в пятимерном пространстве, она, как и множество других формул, не зависит от размерности пространства.

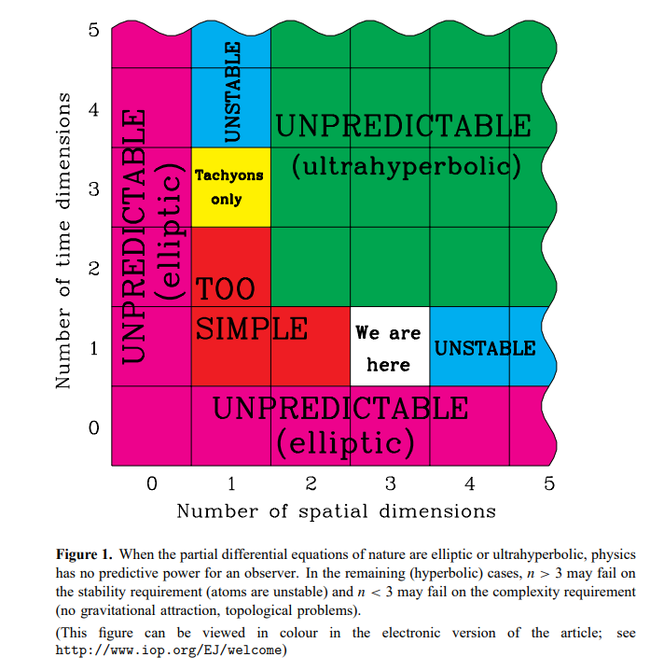
Но даже и без этого всего, мир в 5 мерном пространстве изменится настолько, что в нем не сможет существовать жизнь в том виде, в котором существует в четырехмерном пространстве. Вообще, оказывается, четырехмерный мир – самый простой из возможных и одновременно самый оптимальный для существования в нем жизни, стабильных орбит и химии, какой мы ее знаем.

Книга Кипа Торна, «Интерстеллар. Наука за кадром»

Единственный в своём роде треугольник Шарыгина, открытый лишь в 1982 году

Приветствую Вас, уважаемые Читатели! Сегодня я хочу рассказать об удивительном геометрическом объекте, впервые рассмотренным советским математиком Игорем Федоровичем Шарыгиным.

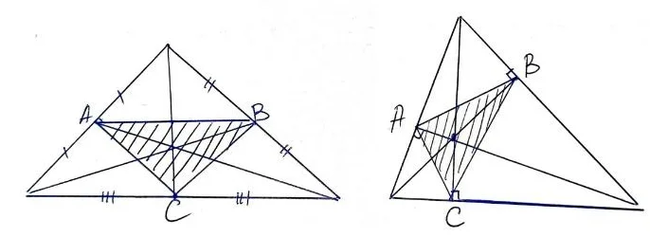
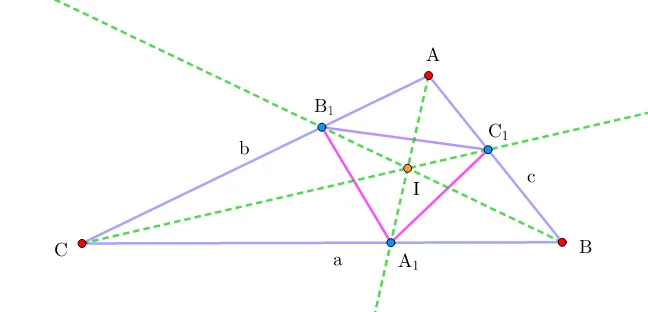
Для начала посмотрите на рисунок ниже. Что Вы на нём видите?

Но, погодите, есть же еще биссектрисы!

И тут становится интересно! Оказывается, и это показал Игорь Федорович, полученный из биссектрис треугольник может быть равнобедренным!

Заметка Шарыгина об этом объекте опубликована в книге «Задачи по геометрии. Планиметрия», 1982.

Впрочем, есть одно очень тонкое условие: угол такого треугольника должен попадать в диапазон от 102,663 до 104,478 градусов!

Основная суть доказательства сводится к рассмотрению подобных треугольников и применению теоремы косинусов, что позволяет получить вот такие выражения для сторон треугольника:

Самим доказательством (доступным каждому школьнику 9 класса!) можно проникнуться в телеграмм-канале «Математика не для всех».

Ответ на пост «Интервью с космонавтом-рекордсменом Геннадием Ивановичем Падалкой о текущем положении российской космонавтики»

Я ни на что не претендую, лишь выскажу свое мнение, которое естественно может и будет отличаться от вашего.

Это на самом деле грустно, но правда.

Мы идем по пути регресса. В микро технологиях быть может еще какие-то подвижки, вернее конвульсии у этой страны есть, но вот в макро технологиях (в т.ч. космос), утеряно давно, модернизации минимальны.

На личном примере расскажу.

Я закончил МГУТУ им. К.Г. Разумовского в 2015 году. Хотел пойти дальше в науку, но не получилось. Собственно почему?

В общем, написав диплом за 2-3 недели аж в начале 5 курса, я стал готовится к аспирантуре. Декан, уверял, что все окей, проблем не будет, там 3 места бюджетных, а желающий только один я.

За 5 лет универского времени, я посетил огромное количество мероприятия (семинары вне вуза, форумы, конференции, встречи с зарубежными (финскими и норвежскими спецами). В целом даже поступали предложения учиться за границей по обмену, но по иным причинам не сложилось.

Попытался устроится в Всероссийский научно-исследовательский институт рыбного хозяйства и океанографии, оставались связи, но там все забито, и в ВНИРО, но там тоже не оказалось мест даже доцентов.

И в итоге, я с красным дипломом, крайне интересной и современной профессией «биоэкология», но в Мск трудно найти работу без связей хотя бы на 30-35 тысяч. Везде ты будешь либо науч.сотрудником на 20к и работать лет 5 таким образом.

Источник