в старинном индийском храме восседали три богини правда ложь и мудрость правда говорит только правду
ГДЗ по информатике 10 класс учебник Босова параграф 22
1. Вы встретили 10 островитян, стоящих по кругу. Каждый из них произнёс фразу: «Следующие 4 человека, стоящие после меня по часовой стрелке, лжецы». Сколько среди них лжецов?
Н Л Л Л Л Н Л Л Л Л
2. Однажды некий путешественник гостил на острове рыцарей и лжецов. Там ему встретились два местных жителя. Путешественник спросил одного из них: «Кто-нибудь из вас рыцарь?» Его вопрос не остался без ответа, и он узнал то, что хотел. Кем был островитянин, к которому путешественник обратился с вопросом, — рыцарем или лжецом? Кем был другой островитянин?
3. В старинном индийском храме восседали три богини: Правда, Ложь и Мудрость. Правда говорит только правду, Ложь всегда лжёт, а Мудрость может сказать правду или солгать. Паломник, посетивший храм, спросил у богини слева: «Кто сидит рядом с тобой?» «Правда», — ответила та. Тогда он спросил у средней: «Кто ты?» «Мудрость», — отвечала она. Наконец он спросил у той, что справа: «Кто твоя соседка?» «Ложь», — ответила богиня. И после этого паломник точно знал, кто есть кто. Определите, на каком месте сидит каждая из богинь.
Если богиня сидящая слева является Правдой, то она не могла сказать что рядом с ней сидит Правда.
Предположим, что Правда сидит в центре, но тогда она не могла сказать про себя что она Мудрость.
Исходя из последнего высказывания по условию задачи и вывода что справа сидит Правда, получаем что в центре сидит Ложь, а слева Мудрость.
Ответ: Мудрость, Ложь, Правда.
4. В симфонический оркестр приняли на работу трёх музыкантов — Борисова, Сергеева и Васечкина, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе. Каждый из музыкантов владеет двумя инструментами.
1) Сергеев — самый высокий;
2) играющий на скрипке меньше ростом играющего на флейте;
3) играющие на скрипке и флейте и Борисов любят пиццу;
4) когда между альтистом и трубачом возникает ссора, Сергеев мирит их;
5) Борисов не умеет играть ни на трубе, ни на гобое.
Выясните, на каких инструментах играет каждый из музыкантов.
Из условий задачи Борисов не играет ни на трубе, ни на гобое, ни на скрипке, ни на флейте. Остается альт, кларнет. Значит Борисов не самый маленький и не самый высокий.
Отсюда Васечкин самый маленький и он играет на скрипке и трубе
Сергеев играет на флейте и гобое
5. В педагогическом институте Аркадьева, Бабанова, Корсакова, Дашков, Ильин и Флёров преподают экономическую географию, английский язык, немецкий язык, историю, французский язык, математику.
1) преподаватель немецкого языка и преподаватель математики в студенческие годы занимались художественной гимнастикой;
2) Ильин старше Флёрова, но стаж работы у него меньше, чем у преподавателя экономической географии;
3) будучи студентками, Аркадьева и Бабанова учились вместе в одном университете. Все остальные окончили педагогический институт;
4) Флёров — сын преподавателя французского языка, но студентом у него не был;
5) преподаватель французского языка — самый старший из всех по возрасту и у него самый большой стаж работы. Он работает в педагогическом институте с тех пор, как окончил его. Преподаватели математики и истории — его бывшие студенты;
6) Аркадьева старше преподавателя немецкого языка.
Кто какой предмет преподаёт?
Аркадьева – французский, Бабанова – немецкий, Корсакова – математика, Дашиков – английский, Ильин – история, Флеров – география.
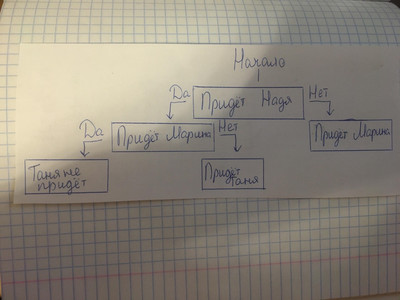
6. На вопрос «Кто из девушек собирается прийти на день рождения к Саше?» был получен уклончивый ответ: «Если Марина придёт на день рождения, то Надя тоже придёт, а Таня не придёт. Если Надя придёт, то Таня придёт в том и только в том случае, если не придёт Марина». Можно ли по этой информации точно установить, кто из девушек придёт к Саше, а кто нет?
7. В бюро переводов приняли на работу троих сотрудников: Диму, Сашу и Юру. Каждый из них знает ровно два иностранных языка из следующего набора: немецкий, японский, шведский, китайский, французский и греческий.
1) ни Дима, ни Юра не знают японского;
2) переводчик с шведского старше переводчика с немецкого;
3) переводчик с китайского, переводчик с французского и Саша родом из одного города;
4) переводчик с греческого, переводчик с немецкого и Юра учились втроём в одном институте;
5) Дима — самый молодой из всех троих, и он не знает греческого;
6) Юра знает два европейских языка.
Укажите имена переводчика с шведского языка и переводчика с китайского языка.
Решение (табличный метод):
составим таблицу, где каждая строка соответствует переводчику, а столбец – языку
Презентация по математике «Задачи про лжецов»
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
На острове Баал живут только люди и странные обезьяны, которых невозможно отличить от людей. Любой из жителей острова говорит или только правду, или только неправду. Кто следующие двое? А: «Б лживая обезьяна. Я человек.» Б: «А сказал правду.» Задача №1
РЕШЕНИЕ: Двойное утверждение, использованное А, верно только при условии, что обе его части верны. Предположим, что В – честный человек, в таком случае А также честен (именно так говорит В), поэтому В – лжец, как утверждает А, что противоречит нашему предположению. Поэтому В – лжец. Прекрасно это осознавая, В сказал, что А – тоже лжец. Таким образом, первое утверждение А является ложью, и В – не лживая обезьяна. Однако В, как мы уже выяснили, – точно лжец, а это значит, что В не обезьяна. В – нечестный человек. Второе утверждение А показывает нам, что А – обезьяна. Следовательно, А – лживая обезьяна.
Решение: Обозначим каждую богиню определённой буквой. В нашем распоряжении следующие утверждения: 1. А говорит, что В – Правда. 2. В говорит, что она Мудрость. 3. С говорит, что В – Ложь. Первое предложение подсказывает нам, что А не Правда. Второе предложение также было сказано не Правдой, следовательно Правда – С. Откуда ясно, что последнее предложение верно: В – Ложь, а А – Мудрость.
Задача № 3 На столе три монеты: золотая, серебряная и медная. Если вы произнесёте утверждение, которое окажется правдой – Вам дадут монету. За неправду Вам не дадут ничего. Что надо сказать, чтобы получить золотую монету?
Решение: «Ты дашь мне ни медную и не серебряную монету». Если это утверждение верно, то мне дадут золотую монету. Если моё утверждение неверно, тогда верным должно быть обратное утверждение, а именно: «Ты дашь мне либо медную, либо серебряную монету». Но тогда это противоречит условиям задания – за ложь монеты давать не должны. Следовательно, первоначальное утверждение верно.
Задача № 4 Вы подъехали к развилке двух дорог. Одна из них ведёт в Лжегород, где находится универсальный магазин разгадок Вселенной, которые отпускают за бесплатно. Другая дорога ведёт в Правдоград, где есть бензоколонка. Жители Лжегорода всегда лгут, а жители Правдограда всегда говорят правду и только правду. На развилке дежурят по одному представителю от каждого из двух городов. Вы не знаете, кто из них откуда. Как узнать, которая дорога ведёт в Правдоград, если вам разрешено задать только один вопрос только одному представителю?
Решение: Существует несколько вариантов подобных вопросов.Косвенный вопрос: «Эй ты! Что скажет тот человек, если я у него спрошу, куда ведет эта дорога?». Ответ на такой вопрос всегда будет противоречить тому, куда дорога ведет в действительности. Вопрос с подковыркой: «Эй ты! Тот человек, что дежурит у дороги, ведущей в Правдоград, он родом оттуда?». Ответ будет положительным только в двух случаях: либо это житель Правдограда, стоящий на дороге в Правдоград, либо житель Лжегорода, стоящий на той же самой дороге. В обоих случаях можно быть уверенным, что при утвердительном ответе это дорога действительно приведёт Вас в Правдоград. Таким же образом можно сформулировать и вопрос с отрицанием. Или же другой, мудрёный вопрос: «Эй ты! Что бы ты сказал, если бы я спросил тебя. ». Житель Правдограда всегда ответит правду, а житель Лжеграда соврёт. Однако благодаря формулировке вопроса лжецу придется соврать два раза, а то есть сказать правду.
Задача №5 Петр лгал с понедельника по среду и говорил правду в другие дни, а Иван лгал с четверга по субботу и говорил правду в другие дни. Однажды они одинаково сказали: «Вчера был один из дней, когда я лгу». В какой день они сказали это?
Решение: Это был четверг. В этот день Петр правдиво сказал, что вчера (т.е. в среду) он лгал, а Иван солгал насчет того, что вчера (т.е. в среду) он лгал, ведь по условию в среду он говорит правду.
Задача №6 Леди Кэт сказала: «Я самая прекрасная. Мэри не самая прекрасная». Джейн сказала: «Кэт не самая прекрасная. Я самая прекрасная». А Мэри просто сказала: «Я самая прекрасная». Белый рыцарь предположил, что все утверждения прекраснейшей из девушек истинны, а все утверждения остальных дам ложны. Исходя из этого, определите прекраснейшую из дам.
Решение: Предположим, что Джейн самая прекрасная. Значит, она говорит правду, а Кэт и Мэри лгут. Но Кэт говорит, что Мэри не самая прекрасная, а Мэри утверждает обратное. Поскольку обе говорят неправду, то они противоречат друг другу. Значит, этот случай невозможен. Если предположить, что Мэри самая прекрасная, то противоречить друг другу будут Джейн и Кэт. Этот случай тоже невозможен. Остается убедиться, что если Кэт говорит правду, то никаких противоречий не возникает, и она действительно самая прекрасная.
Задача №7 Красный рыцарь поймал вора Джона с женским кошельком. Джон признался, что встретил на улице леди Джейн, леди Лину и леди Катерину и украл кошелек у одной из них. Вечером в замок Красного рыцаря прибыл гонец и сказал: «Мою госпожу ограбили». «Кого ограбили?» —спросил рыцарь. «Леди Катерину», — сказал гонец. Кому рыцарь должен вернуть кошелек, если ему известно, что гонец леди Джейн всегда говорит правду, гонец леди Лины всегда лжет, а гонец леди Катерины через раз говорит то правду, то ложь?
Решение: Если бы в замок прибыл гонец леди Джейн, он бы оба раза сказал правду, то есть сообщил бы, что ограбили леди Джейн. Если бы в замок прибыл гонец леди Катерины, то он мог сказать правду только один раз. Но в его случае высказывания «ограбили мою госпожу» и «ограбили леди Катерину» означают одно и то же, поэтому он мог либо оба раза сказать правду, либо оба раза солгать. Значит, в замок прибыл гонец леди Лины и оба раза солгал. То есть на самом деле ограбили не его госпожу и не леди Катерину, а леди Джейн.